cs224n笔记(一) Lecture1: word2vec算法详细解析

本文是对斯坦福CS224N关于word2vec内容的学习笔记

1. 背景知识

词向量除了可以分为离散型和分布型，还可以分为计数型和预测型，计数型的如离散型中的词典模型（BOW），TF-IDF模型，以及分布型中的n-gram，他们本质上都是在计算词序列出现的频次，属于统计模型，没有可学习的参数，而word2vec则是直接建立可训练的模型进行预测，模型中的参数和词向量都是通过学习得到，词向量中隐式地编码了语料库中的语义信息。

2. 基本原理

在word2vec中，词向量的长度不再与词典的大小相关，通常是人为设定成300以内，向量中的数值也不再是离散型数值，也更不是one-hot，每个位置都是连续型变量。和n-gram原理 类似，word2vec也需要建立统计语言模型，n-gram中是用第i个词前的m个词来预测第i个词应该是什么，word2vec也类似，不过它会涉及第i+1、i+2…i+m个词，即中心词周边的2m个词$w_{i-m},...,w_{i-1},w_{i+1},...,w_{i+m}$。可以根据周边词来预测中心词，也可以根据中心词来预测周边词，前者称为CBOW模型，后者称为skip-gram模型。

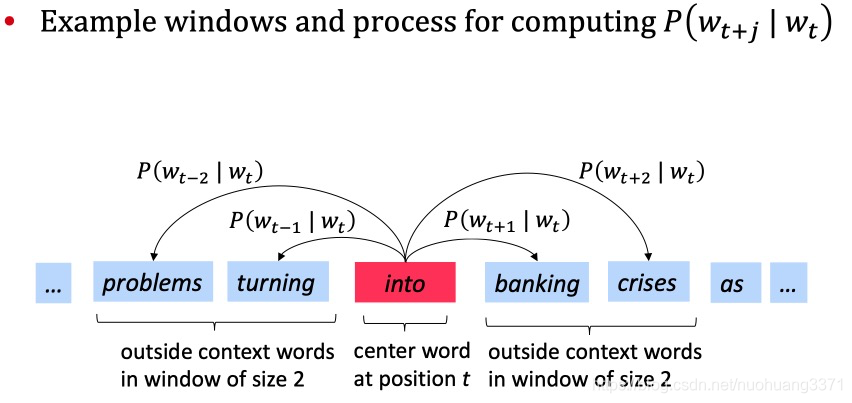
skip-gram模型示意图，CBOW的示意图就是将途中的箭头反过来

1. CBOW

如前面所述，CBOW用周边词来预测中心词，下面将用数学语言进行整个模型的推导。

首先明确一下word2vec中模型参数和词向量的概念，它们本质上是一回事，但是实现时却分开成了两套变量，词典中的每个词都会对应两个向量，一个姑且称为参数向量，当一个词作为模型输入用去预测别的词时，就用参数向量来表示该词，因为它是作为模型的输入，因此称为输入向量也可以，下面的符号约定中也提到一般用v来表示；另一个称为词向量，它是模型的输出，也即是我们想得到的东西，同理，也可以称之为输出向量，一般用u表示。

上述套概念在skip-gram和CBOW都适用，但是因为这两个模型的输入和输出刚好是相反的，因此千万要注意别把符号弄混了。具体为什么一个词要设置两套变量？CS224N中说是这样做方便计算、方便求导，实际上最后这两套向量都可以作为输出结果，甚至可以平均合并。

其次约定一些符号表示

• 词典为$V$，词典的大小为$|V|$
• 窗口大小为$m$，词向量大小为$n$
• 一个词如果用它作为中心词，下标用小写字母$c$表示，代表center，如果它作为周边词，则用小写字母$o$表示，表示outside
• 词用$w$表示，词向量用$u$或者$v$表示，并且约定当词向量是作为模型输入时，用$v$来表示这个词向量，如果作为模型输出，则用$u$来表示；因此在skip-gram中，$u$是用来表示周边词的，$v$是用来表示中心词的，而CBOW则相反，$u$表示中心词，而$v$表示周边词；为了不弄混，还是用向量是作为模型的输入还是输出作为区分最为清晰。
• $\mathcal{V}$用来表示词典中所有词对应的输入向量组成的矩阵，用$\mathcal{U}$表示输出向量对应的矩阵，那么这两个矩阵的大小均为$|V|\times n$
• $W$依旧表示模型的参数，当然word2vec中，模型参数和词向量是一回事，因此这里的$W$也就是$\mathcal{V}$以及$\mathcal{U}$
• x表示词w的one-hot向量，它为列向量，长度与词典的大小|V|相同，它作为输入层的输入，从代码层面来说它才是真正的输入向量，用它与$\mathcal{V}$相乘可以得到词w对应的输入向量v，tensorflow中的embedding层就是进行该操作。

最后开始推导：

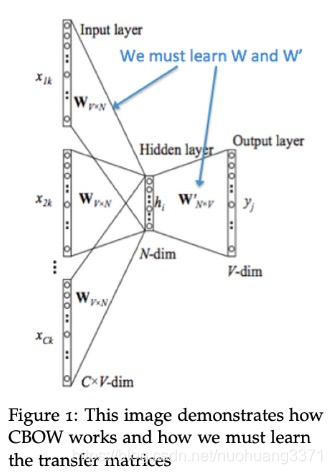
CBOW的模型示意图，x为输入词对应的one-hot列向量，$W_{V\times N}$就是$\mathcal{V}$，$W_{V\times N}^{\prime }$就是$\mathcal{U}$

算法流程：

1. 输入为窗口中除了中心词外的所有词的one-hot向量：$(x_{c-m},...,x_{c-1},x_{c+1},...,x_{c+m})$
2. 将one-hot向量与输入矩阵$\mathcal{V}$做矩阵乘法，得到窗口内每个词对应的输入词向量，即$v_{c-m}=\mathcal{V}{x}_{c-m}，v_{c-1}=\mathcal{V}{x}_{c-1}，...，v_{c+1}=\mathcal{V}{x}_{c+m}，v_{c+m}=\mathcal{V}{x}_{c+m}$，
3. 将窗口内所有的输入向量做平均池化，作为模型输入，$\hat{v}=\frac{v_{c-m}+...+v_{c-1}+v_{c+1}+...+v_{c+m}}{2m}$
4. 计算$\hat{v}$与词典中每个词向量求点积，得到$z$，$z=\mathcal{U}\hat{v}$，$z$也为列向量，长度为词典大小$|V|$
5. 将$z$送入softmax层进行概率归一化得到$\hat{y}$，$\hat{y}$中每一个位置的数值对应词典中每一个词被预测为中心词的概率。
6. 用模型输出的预测概率$\hat{y}$与真实概率$y$计算损失，一般用交叉熵损失即可。$y$是窗口内真实中心词所对应的one-hot向量，长度也为$|V|$

算法解析：

算法流程第4点中求点积可以理解为求输入向量与词典中每个向量的余弦距离，也可以理解为相似度，点积的结果越大，表示两个向量越相似，从特征语义的角度来说，就是从词典中找到一个与上下文语义最相近的词语；词典中每个词都会对应一个余弦距离，余弦距离最大的那个词就是最有可能的中心词预测，但是由于余弦距离不能作为概率，因此在算法流程第5点中进行了softmax归一化。

算法流程4、5、6点可以归结为一条公式：

$$\begin{array}{rl}Loss=& -\sum _{j=1}^V{y}_{j}log\widehat{y_j}\\ =& -y_{c}log\widehat{y_c}\\ =& -log\widehat{y_c}\\ =& -log\frac{exp(u_c^T\hat{v})}{{\sum }_{k=1}^{|V|}exp(u_k^T\hat{v})}\end{array}$$

$y$，$\hat{y}$都是向量，加了下标表示向量中某一个位置上的值。公式中的第一行就是标准的交叉熵损失表达式，由于y是一个one-hot向量，只在特定的位置为1，结合CBOW模型的含义，$y$向量在中心词$w_c$对应的位置$y_c$上为1，只有当$j=c$时，求和公式的加数才不为0，因此第一行可简化为第二行，又由于$y_c$其实就是1，干脆可以不写，于是简化为第三行，最关键的地方就是如何表示$\widehat{y_c}$。算法流程第5行提到是通过对点积z进行softmax归一化而得到$\hat{y}$，因此公式第四行其实就是一个求softmax概率然后求负对数，softmax概率即其中的分式，它的含义是模型预测中心词为$w_c$的概率。算法流程第5行中计算的是$z=\mathcal{U}\hat{v}$，z也是一个向量，具体到某一个值如$z_c$时，就是取出矩阵$\mathcal{U}$的第$c$行，然后计算$z_c=u_c^k\hat{v}$

2. skip-gram

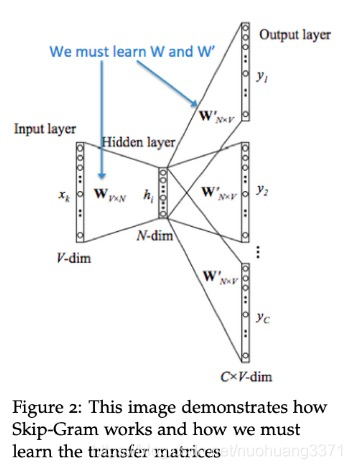
和CBOW有些不同，skip-gram是用中心词预测周边词，窗口内的中心词只有一个，因此输入只有一个向量，周边词涉及多个位置，因此模型有多个输出向量，每个向量对应周边的一个位置。

算法流程：

1. 输入为中心词，中心词对应的one-hot向量：$x_c$
2. 将one-hot向量与输入矩阵$\mathcal{V}$做矩阵乘法，得到中心词入词向量，即$v_c=\mathcal{V}{x}_c$，
3. 计算$v_c$与词典中每个词向量求点积，得到$z$，$z=\mathcal{U}{v}_c$，$z$也为列向量，长度为词典大小$|V|$
4. 将$z$送入softmax层进行概率归一化得到$\hat{y}$，并且每一个周边词都会对应一个预测概率，即${\hat{y}}_{c-m},{\hat{y}}_{c-1},...,{\hat{y}}_{c+1},{\hat{y}}_{c+m}$，窗口有多大就得计算多少次softmax概率
5. 用模型输出的每个预测概率${\hat{y}}_{c-m},{\hat{y}}_{c-1},...,{\hat{y}}_{c+1},{\hat{y}}_{c+m}$与真实概率$y_{c-m},y_{c-1},...,y_{c+1},y_{c+m}$分别计算交叉熵损失并求和，同理$y_{c-m},y_{c-1},...,y_{c+1},y_{c+m}$也都是one-hot向量。

算法解析：

skip-gram的流程与CBOW差别不大，只是输入向量变成了一个，省去了均值池化，输出向量变成了多个，每个周边词都要计算一次softmax概率并分别计算损失，最后叠加。因为同样是用交叉熵损失，因此和CBOW的公式推导没有太大区别，下面直接引用CBOW中公式推导前三行的简化结果，得到skip-gram的损失函数为：

$$\begin{array}{rl}Loss& =-\sum _{j=-m;j!=0}^{m}log{\hat{y}}_{c+j}\\ & =-\sum _{j=-m;j!=0}^{m}log\frac{exp(u_{c+j}^T{v}_c)}{{\sum }_{k=1}^{|V|}exp(u_k^T{v}_c)}\end{array}$$

不要被庞杂的符号吓到，其实还是softmax概率取负对数，只不过每个周边词都要计算一次，下标有些复杂就是因为要对应每个周边词的位置，log里的分母跟CBOW模型中没什么区别，还是需要用输入向量与词典中所有词求一次点积。

上面这条公式是CS224N的notes中的写法，在slides对于softmax概率有一个另一种写法，即：

$$P(o|c)=\frac{exp(u_o^T{v}_c)}{{\sum }_{w\in V}exp(u_w^T{v}_c)}$$

其实整体结构是一样的，只是换了一批符号而已，这一点不需要体纠结。

需要注意在slides中的推导逻辑和上面有些许不同，它的逻辑是：skip-gram是在构建一个统计语言模型，具体来说是求一个含有未知参数的概率分布，这类问题最直接的方法就是用最大似然函数来求这个概率的分布的参数，即：

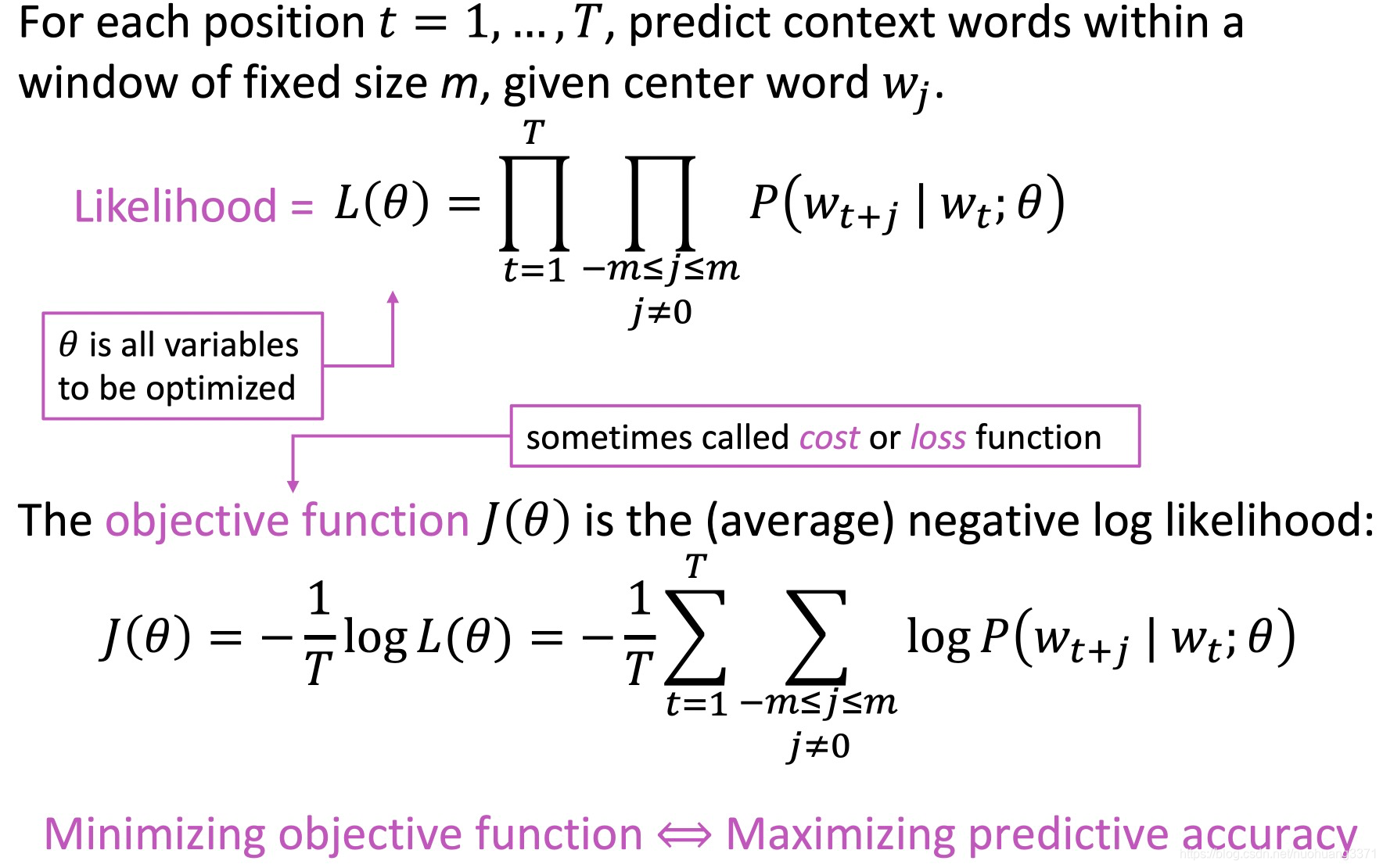
它是先得出最大似然函数，然后将最大似然函数转为损失函数，转的方法为取对数简化计算，并且加负号转变任务：使似然函数最大化转成使损失函数最小化，这么一通转化后损失函数的形式和交叉熵损失一样，这也就和notes中的写法一致了。但是依然需要注意的是slides和notes的推导逻辑是不一样的，尽管在这里殊途同归了，但是最大似然函数和交叉熵损失并不一样，只是对数似然函数经常会取负对数简化计算，使得最终要优化的形式和交叉熵损失一致。

3.维度爆炸的处理

不管是CBOW还是skip-gram，最后计算softmax概率时都会涉及整个词典V，词典中的每个词的词向量都会被用到，这涉及巨大的计算量，为了解决这一点有两种做法，一个用一种很常见的操作是negative-sampling，另一个是huffman-tree霍夫曼树方法。

1. negative sampling

基本原理：negative samplingskip-gram的方法优化的目标跟前面相比有所变化，是判断给定的样本对是正样本对还是负样本对。以skip-gram为例，skip-gram用中心词预测周边词，假设半窗口大小为$m$，那么在一个窗口内的正样本对$(w_o,w_c)$有$2m$对，负样本有 $|V|-2m$对，词典中除了周边词外的所有词与中心词组成的样本对都是负样本对。所谓正样本对表示正表示在给定窗口内，$w_c$作为中心词，$w_o$是它的周边词，而负则表示$w_o$没有出现在$w_c$的周边。由于负样本太多，实际上对于每个窗口的训练只需要取其中一部分负样本对即可，不用考虑整个词典。

建模过程：

基于上述描述，我们要求的概率模型可以表述为$P(D|w_o,w_c,\theta )$，$D=1$表示$w_o$和$w_c$为正样本对，$D=0$表示$w_o$和$w_c$为负样本对，$\theta$表示概率模型的未知参数，在word2vec中它就是前面所说的参数向量和词向量。那么如何表示$P(D|w_o,w_c,\theta )$？在word2vec原论文中还是用周边词的词向量和中心词的参数向量进行点积运算，但不再适用softmax函数进行归一化得到概率值，而是采用sigmoid函数直接将点积结果转化为$(0,1)$间的概率值。

我们用$\sigma$表示sigmoid函数，sigmoid函数需要谨记三个关键公式：

$$\begin{array}{rl}\sigma (x)& =\frac{1}{1+e^{-x}}\\ \sigma (-x)& =1-\sigma (x)\\ {\sigma }^{\prime }(x)=& \sigma (x)(1-\sigma (x))\end{array}$$

则$P(D|w_o,w_c,\theta )$可以表示为：

$$\begin{array}{rl}P(D=1|w_o,w_c,\theta )& =\sigma (u_o^T{v}_c)\\ P(D=0|w_o,w_c,\theta )& =1-P(D=1|w_o,w_c,\theta )\\ & =1-\sigma (u_o^T{v}_c)\\ & =\sigma (-u_o^T{v}_c)\end{array}$$

接下来就是求概率模型的未知参数$\theta$，还是可以用极大似然法，先写出似然函数：

$$likehood(\theta )=\prod _{(w_o,w_c)\in \mathcal{D}}P(D=1|w_o,w_c,\theta )\prod _{(w_o,w_c)\in \tilde{\mathcal{D}}}P(D=0|w_o,w_c,\theta )$$

其中$\mathcal{D}$表示正样本对集合，$\tilde{\mathcal{D}}$表示负样本对集合，对于正样本对集合内的样本对，我们希望预测为$D=1$的概率越大越好，对于负样本对集合内的，我们则希望预测$D=0$的概率越大越好，这样就表示概率模型能够很好地判断给定样本对是正还是负。

有了似然函数下面就是求取参数$\theta$使似然函数取极大值，照例还是可以取负对数，转为极小值问题，并将连乘转为求和简化计算，即：

$$\begin{array}{rl}\underset{\theta }{\mathrm{argmax}}likehood(\theta )& =\underset{\theta }{\mathrm{argmin}}-log(likehood(\theta ))\\ & =\underset{\theta }{\mathrm{argmin}}-(\sum _{(w_o,w_c)\in \mathcal{D}}logP(D=1|w_o,w_c,\theta )+\sum _{(w_o,w_c)\in \tilde{\mathcal{D}}}logP(D=0|w_o,w_c,\theta ))\\ & =\underset{\theta }{\mathrm{argmin}}-(\sum _{(w_o,w_c)\in \mathcal{D}}log\sigma (u_o^T{v}_c)+\sum _{(w_o,w_c)\in \tilde{\mathcal{D}}}log\sigma (-u_o^T{v}_c))\\ & =\underset{\theta }{\mathrm{argmin}}-(\sum _{(w_o,w_c)\in \mathcal{D}}log\frac{1}{1+exp(-u_o^T{v}_c)}+\sum _{(w_o,w_c)\in \tilde{\mathcal{D}}}log\frac{1}{1+exp(u_o^T{v}_c)})\end{array}$$

更具体一点，假设半窗口大小为$m$，负样本对只采样$K$对，则正样本对集合$\mathcal{D}$中有$2m$个样本，负样本对集合$\tilde{\mathcal{D}}$中有$K$对样本，这些样本共同组合形成一个窗口内（一个batch）的训练数据，则上式可以更具体化地写成：

$$\underset{\theta }{\mathrm{argmin}}-(\sum _{j=-m;j!=0}^{+m}log\frac{1}{1+exp(-u_j^T{v}_c)}+\sum _{k=1}^{K}log\frac{1}{1+exp(u_k^T{v}_c)})$$

现在的问题在于用什么方式抽取负样本，word2vec采用的带权采样，每个词都对应一个被抽取的概率，这个概率与该词在语料库中出现的次数直接相关，即遵循：

$$P(w)=\frac{counter(w)}{{\sum }_{u\in V}counter(u)}$$

其中，$counter(w)$表示词$w$在语料库中出现的频次，但是在word2vec论文中还加了个3/4幂次，这会略微降低高频词被抽取的概率，略微提高低频词被抽取的概率，即：

$$P(w)=\frac{[counter(w){]}^{3/4}}{{\sum }_{u\in V}[counter(u){]}^{3/4}}$$

在源代码中，是开辟一个片大小为$M$的数组，并在数组中放入词典中的词，每个词放的个数为$M\times P(w)$，在采样时随机生成一个$[0,M-1]$间的整数，通过该整数从数组取出对应的词。

2. huffman tree

4. 参考文献

1. CS224N lecture 1 notes & slides
2. CS224N lecture 2 slides
3. word2vec中的数学原理