文章目录
简介
这个内容也是新的,Attack and Defense
• We seek to deploy machine learning classifiers not only in the labs, but also in real world.
• The classifiers that are robust to noises and work “most of the time” is not sufficient.
• We want the classifiers that are robust the inputs that are built to fool the classifier.光强不够,还要应付人类的恶意攻击
• Especially useful for spam classification, malware detection, network intrusion detection, etc.
公式输入请参考:在线Latex公式
Attack(重点)
攻击是重点,因为防御目前还是比较困难的。
做法

如果在原图片(
x
0
x^0
x0)上加上一些噪音(
Δ
x
\Delta x
Δx)。这些噪音不是从高斯分布来的。然后丢到模型里面,会得到不一样的结果。

Loss Function for Attack
先看普通的训练模型:

训练的目标函数是:
L
t
r
a
i
n
(
θ
)
=
C
(
y
0
,
y
t
r
u
e
)
L_{train}(\theta)=C(y^0,y^{true})
Ltrain(θ)=C(y0,ytrue)
C代表交叉熵,x是不变的,找到参数
θ
\theta
θ,使得输出的分布和标签的分布越接近越好。
如果是Non-targeted Attack:

L
(
x
′
)
=
−
C
(
y
′
,
y
t
r
u
e
)
L(x')=-C(y',y^{true})
L(x′)=−C(y′,ytrue)
这里参数
θ
\theta
θ是不变的,我们希望找到一个
x
′
x'
x′,使得输出
y
′
y'
y′与标签的分布越远越好。
如果是Targeted Attack,就是希望机器将输入错误的分类为
y
f
a
l
s
e
y^{false}
yfalse
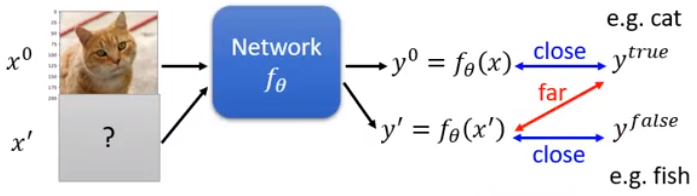
L
(
x
′
)
=
−
C
(
y
′
,
y
t
r
u
e
)
+
−
C
(
y
′
,
y
f
a
l
s
e
)
L(x')=-C(y',y^{true})+-C(y',y^{false})
L(x′)=−C(y′,ytrue)+−C(y′,yfalse)
由于这里是有目标的,所以希望找到一个
x
′
x'
x′,使得输出
y
′
y'
y′与正确标签的分布越远越好,同时与错误(目标)标签越近越好。
当然还要有一个限制,我们不希望攻击被发现,因此输入不能改变太大,不然直接输入鱼就ok了:
d
(
x
0
,
x
′
)
≤
ϵ
d(x^0,x')\le\epsilon
d(x0,x′)≤ϵ

约束的定义
这里我们用
Δ
x
\Delta x
Δx表示
x
0
,
x
′
x^0,x'
x0,x′的差异

计算方式有几种:
1.L2-norm
d
(
x
0
,
x
′
)
=
∣
∣
x
0
−
x
′
∣
∣
2
=
(
Δ
x
1
)
2
+
(
Δ
x
2
)
2
+
(
Δ
x
3
)
2
+
.
.
.
d(x^0,x')=||x^0-x'||_2=(\Delta x_1)^2+(\Delta x_2)^2+(\Delta x_3)^2+...
d(x0,x′)=∣∣x0−x′∣∣2=(Δx1)2+(Δx2)2+(Δx3)2+...
2.L-infinity
d
(
x
0
,
x
′
)
=
∣
∣
x
0
−
x
′
∣
∣
∞
=
m
a
x
{
Δ
x
1
,
Δ
x
2
,
Δ
x
3
,
.
.
.
}
d(x^0,x')=||x^0-x'||_\infty=max\{\Delta x_1,\Delta x_2,\Delta x_3,...\}
d(x0,x′)=∣∣x0−x′∣∣∞=max{Δx1,Δx2,Δx3,...}

L2没有办法描述上面的改变,L-infinity则可以。
3.其他方法
如何攻击
Just like training a neural network, but network parameter 𝜃 is replaced with input
x
′
x'
x′
x
∗
=
a
r
g
m
i
n
d
(
x
0
,
x
′
)
≤
ϵ
L
(
x
′
)
x^*=arg\underset{d(x^0,x')\le\epsilon}{min}L(x')
x∗=argd(x0,x′)≤ϵminL(x′)
这个看上去貌似不好解,我们可以把约束去掉来解:
x
∗
=
a
r
g
m
i
n
L
(
x
′
)
x^*=arg\underset{}{min}L(x')
x∗=argminL(x′)
用GD来弄,这里是对x进GD:

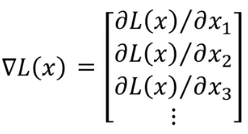
然后加入约束:

每次更新了
x
t
x^t
xt后判断是否满足条件,如果不满足,那么对
x
t
x^t
xt进行修正,使其满足限制条件。修正函数如下:

思想是穷举所有满足约束条件的x,找一个离
x
t
x^t
xt最近的x来替换
x
t
x^t
xt。可视化后:

例子
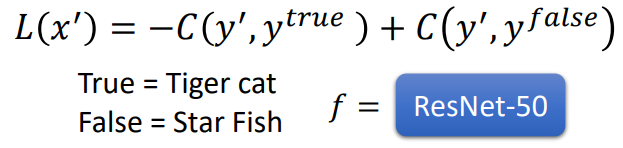
攻击结果如下:

看上去新图片没有什么区别,但是我们用原图片减新图片,然后乘以50倍:

下面是把猫变成键盘的例子:

如果不是加入攻击噪音,那么结果是:

小结
横坐标代表输入,纵坐标代表输出,也就是x属于某个分类的概率:
x
0
x^0
x0是高维空间中的一个点,在这个高维空间中,有一些神奇的方向,能够使得
x
0
x^0
x0稍微变化一点点(下面第二张图中,红色部分非常尖,稍微移动就会到别的地方),会让机器认为图片中的猫是其他东西。


其他方法Attack Approaches
• FGSM (https://arxiv.org/abs/1412.6572)
• Basic iterative method (https://arxiv.org/abs/1607.02533)
• L-BFGS (https://arxiv.org/abs/1312.6199)
• Deepfool (https://arxiv.org/abs/1511.04599)
• JSMA (https://arxiv.org/abs/1511.07528)
• C&W (https://arxiv.org/abs/1608.04644)
• Elastic net attack (https://arxiv.org/abs/1709.04114)
• Spatially Transformed (https://arxiv.org/abs/1801.02612)
• One Pixel Attack (https://arxiv.org/abs/1710.08864)
• …… only list a few
不同的攻击方法只不过是损失函数中的约束
d
(
x
0
,
x
′
)
≤
ϵ
d(x^0,x')\le\epsilon
d(x0,x′)≤ϵ不同,以及最小化的优化方法不一样而已,下面我们来看看一种FGSM
FGSM
Fast Gradient Sign Method虽然不是最强大的,但是它是非常简单的一种方法。
x
∗
←
x
0
−
ϵ
Δ
x
x^*\leftarrow x^0-\epsilon\Delta x
x∗←x0−ϵΔx
Δ
x
=
[
s
i
g
n
(
∂
L
/
∂
x
1
)
s
i
g
n
(
∂
L
/
∂
x
2
)
s
i
g
n
(
∂
L
/
∂
x
3
)
⋮
]
o
n
l
y
h
a
v
e
+
1
o
r
−
1
\Delta x=\begin{bmatrix} sign(\partial L/\partial x_1)\\ sign(\partial L/\partial x_2) \\ sign(\partial L/\partial x_3)\\\vdots \end{bmatrix}\\ only\space have\space +1\space or\space -1
Δx=⎣⎢⎢⎢⎡sign(∂L/∂x1)sign(∂L/∂x2)sign(∂L/∂x3)⋮⎦⎥⎥⎥⎤only have +1 or −1
例如
∂
L
/
∂
x
1
>
0
\partial L/\partial x_1>0
∂L/∂x1>0,无论是多少,都取:
s
i
g
n
(
∂
L
/
∂
x
1
)
=
1
sign(\partial L/\partial x_1)=1
sign(∂L/∂x1)=1
也就是说这个算法的思想就是只攻击一次就好(这个是一拳超人?就是攻击一次的意思?)

也有文献说多攻击几次效果更好,那是另外一种FGSM方法,这里不考虑。
从图形上看,如果是普通的GD,我们是先算gradient的方向,然后把
x
0
x^0
x0更新到
x
1
x^1
x1。
现在FGSM是直接按照gradient的方向,一步直接更新到对应方向的右上角
x
∗
x^*
x∗,(只要gradient的方向是第三象限的范围
x
∗
x^*
x∗都是右上角那个点,同理,如果只要gradient的方向是第二象限
x
∗
x^*
x∗都是右下角那个点)
也就是说FGSM只在意gradient的方向,不在意它的大小。

因为如果是普通的GD,配上比较大的LR的时候,会出现下图的情况。这个就会超出限制条件,按照之前的讲法,要把它拉回来(就是右上角那个点)。
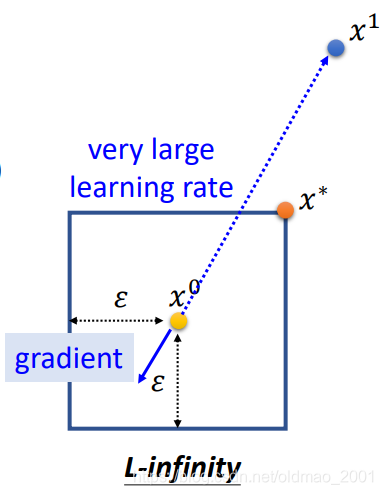
White Box v.s. Black Box
上面讲的攻击方式是白盒攻击,因为我们需要知道模型参数:
• In the previous attack, we fix network parameters 𝜃 to find optimal
x
′
x'
x′
• To attack, we need to know network parameters 𝜃
• This is called White Box Attack.
那么我们如果保护好模型的参数,是否就会安全?
NO!,还可以做黑盒攻击。
Black Box Attack
攻击步骤如下:
1、现在有一个我们不知道参数的黑盒模型(深蓝色);
2、我们用训练黑盒模型的训练数据自己训练一个代理模型(浅蓝色);
3、用代理模型生成一个攻击对象(图片);
4、用攻击对象去攻击黑盒模型。

那是不是意味我们还要保护好训练数据呢?
不行。如果模型是一在线的图像识别系统,那么我们自己做一组图片数据,丢到线上模型中,得到一组对应的标签,用这个作为训练数据来训练代理模型即可。
目前已经有相应的文章:https://arxiv.org/pdf/1611.02770.pdf

这里显示了用同一个代理模型还可以去攻击不同黑盒模型。这个攻击甚至可以泛化到:
Universal Adversarial Attack
根据之前说的攻击方法,不同的图片是需要不同的
Δ
x
\Delta x
Δx才能成功攻击。但是研究表明,不同图片实际上可以用同一个攻击对象来进行攻击。
参考文献:https://arxiv.org/abs/1610.08401

Adversarial Reprogramming
本来模型是用来做图像识别的(任务A),但是经过Reprogramming ,模型却变成根据方块数量来分类(任务B)
方块数量多少对应的分类如下图:

我们并不对模型本身进行改变,而是把方块周围加上噪音(合成):

然后把合成结果丢到模型,就得到相应的分类:

参考文献:Gamaleldin F. Elsayed, Ian Goodfellow, Jascha Sohl-Dickstein, “Adversarial Reprogramming of Neural Networks”, ICLR, 2019
Attack in the Real World
现实应用中,模型部署后是通过摄像头来捕捉输入的,因此可以把噪音打印出来进行攻击。
文献:https://www.cs.cmu.edu/~sbhagava/papers/face-rec-ccs16.pdf
理论结果:

做出来的眼镜:

作者(最左边两个)戴上眼镜后模型识别的结果:

当然作者做了很多工作:
- An attacker would need to find perturbations that generalize beyond a single image.
人脸识别会包含很多角度,因此攻击对象也要考虑多个角度,不能只有正面才能攻击。 - Extreme differences between adjacent pixels in the perturbation are unlikely to be accurately captured by cameras.
要确保攻击对象所包含的噪音能被摄像头捕捉到,因此需要噪音包含比较大的色块。 - It is desirable to craft perturbations that are comprised mostly of colors reproducible by the printer.
需要考虑现实世界中存在的颜色。
除了人脸识别,还有针对交通标志识别的攻击(https://arxiv.org/abs/1707.08945):

除了对图片进行攻击,还有别的方式的攻击:
针对声音:
https://nicholas.carlini.com/code/audio_adversarial_examples/
https://adversarial-attacks.net/
针对文字:
https://arxiv.org/pdf/1707.07328.pdf

Defense防御
Adversarial Attack cannot be defended by weight regularization, dropout and model ensemble.
上面讲攻击的时候有研究表明攻击是可以跨模型的,因此对模型做ensemble并不能很好的防御攻击。
防御主要有两种方式:
• Passive defense: Finding the attached image without modifying the model.
被动防御方式:不改变当前的模型及参数,而是在模型的外面做一层防护,这个防护要找出那些奇怪的图片,这块内容应该有在Special case of Anomaly Detection中有提到。
• Proactive defense: Training a model that is robust to adversarial attack.
主动防御方式:是直接增加模型的鲁棒性来防御攻击。
Passive Defense
加的防护罩就是filter,这个filter不用很复杂,很简单就可以做到防护,例如:平滑

看下具体结果,因为这个猫之前有做过实验,直接在之前的基础上做即可:
原图过filter后识别效果:

攻击对象过filter后识别效果:

可以看到,只是几率稍微下降一点。因为filter并不会改变原来的图片,而是改变了攻击的噪音。
Feature Squeeze
文献:https://arxiv.org/abs/1704.01155
Squeeze 实际上就是不同的filter,如果一个图片不做Squeeze 的结果和做Squeeze 的结果相差很多,说明图片是被攻击过的。

Randomization at Inference Phase
https://arxiv.org/abs/1711.01991
在识别之前对图片做一些随机的变换(不能太大,过大可能会影响识别结果):变换大小、填充等。

Proactive Defense
主动防御的思想就是找到漏洞,然后补起来。
假设有训练集:
X
=
{
(
x
1
,
y
^
1
)
,
(
x
2
,
y
^
2
)
,
⋯
,
(
x
N
,
y
^
N
)
}
X=\{(x^1,\hat y^1),(x^2,\hat y^2),\cdots,(x^N,\hat y^N)\}
X={(x1,y^1),(x2,y^2),⋯,(xN,y^N)}
我们用X来训练模型。这是一般的流程,接下来要找漏洞,要再训练T个循环,每个循环中都要找出每个输入图片
x
n
x^n
xn的攻击对象
x
~
n
\tilde x^n
x~n,然后把攻击对象
x
~
n
\tilde x^n
x~n标记对应的类别标签得到新的训练集
X
′
=
{
(
x
~
1
,
y
^
1
)
,
(
x
~
2
,
y
^
2
)
,
⋯
,
(
x
~
N
,
y
^
N
)
}
X'=\{(\tilde x^1,\hat y^1),(\tilde x^2,\hat y^2),\cdots,(\tilde x^N,\hat y^N)\}
X′={(x~1,y^1),(x~2,y^2),⋯,(x~N,y^N)},再用X’来训练模型。

这个方式有很大的缺点就是如果我们用算法A来找漏洞和补漏洞,如果用算法B来攻击,模型是无法防护的。
因此如果黑客知道我们的算法A,就会想办法用新方法来进行攻击。
所以目前防御是比较弱的。
总结
• Attack: given the network parameters, attack is very easy.
• Even black box attack is possible
• Defense: Passive & Proactive
• Future: Adaptive Attack / Defense
To learn more …
• Reference
https://adversarial-ml-tutorial.org/ (Zico Kolter and Aleksander Madry)
• Adversarial Attack Toolbox:
https://github.com/bethgelab/foolbox
https://github.com/IBM/adversarial-robustness-toolbox
https://github.com/tensorflow/cleverhans

























 7223
7223

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










