高等数学：函数（函数概念、定义域）

风吹迎面入袖凉

已于 2024-05-02 20:15:13 修改

阅读量7.3k

点赞数 36

分类专栏：高等数学文章标签：笔记经验分享其他

于 2024-04-25 20:08:10 首次发布

本文链接：https://blog.csdn.net/panda_aaa/article/details/138183285

版权

高等数学专栏收录该内容

8 篇文章

订阅专栏

作者是一名在校学生，刚开始学习高数时不知从何下手，出此文章，一是希望能够帮助大家用最短的时间把高数知识点掌握；二是把我在学习高数过程中遇到的一些问题和心得分享给大家，若能对您有所帮助，万分荣幸，若有不对的地方，敬请见谅！

本文章纯手敲狂肝持续更新中，望转载时标明出处或@作者 ，谢谢谢谢！
如果您发现本文章由任何地方讲解有误，愿意通过私信或留言告诉我的话，我将万分感谢！

函数

一、函数的定义

y=f(x) 形如这种样子的咱们就叫它函数，其中x叫做自变量，y叫做因变量。按照我的理解来的话咱们可以把 f（□）看做是一个榨汁机，假如手中有一根甘蔗，咱们把它放到括号里面就可以得到一杯甘蔗汁，例如：甘蔗汁=榨汁机（甘蔗）

在这里插入图片描述

当我们把甘蔗放到榨汁机里面得出来的必然是一杯甘蔗汁，而不是其他的东西，按照书上的概念来说就是有一个x放进f（）的时候，得出来的必然只有一个y。f（x）和y是对应的，不能出现一个一对多，不然就不是函数了

图解如：

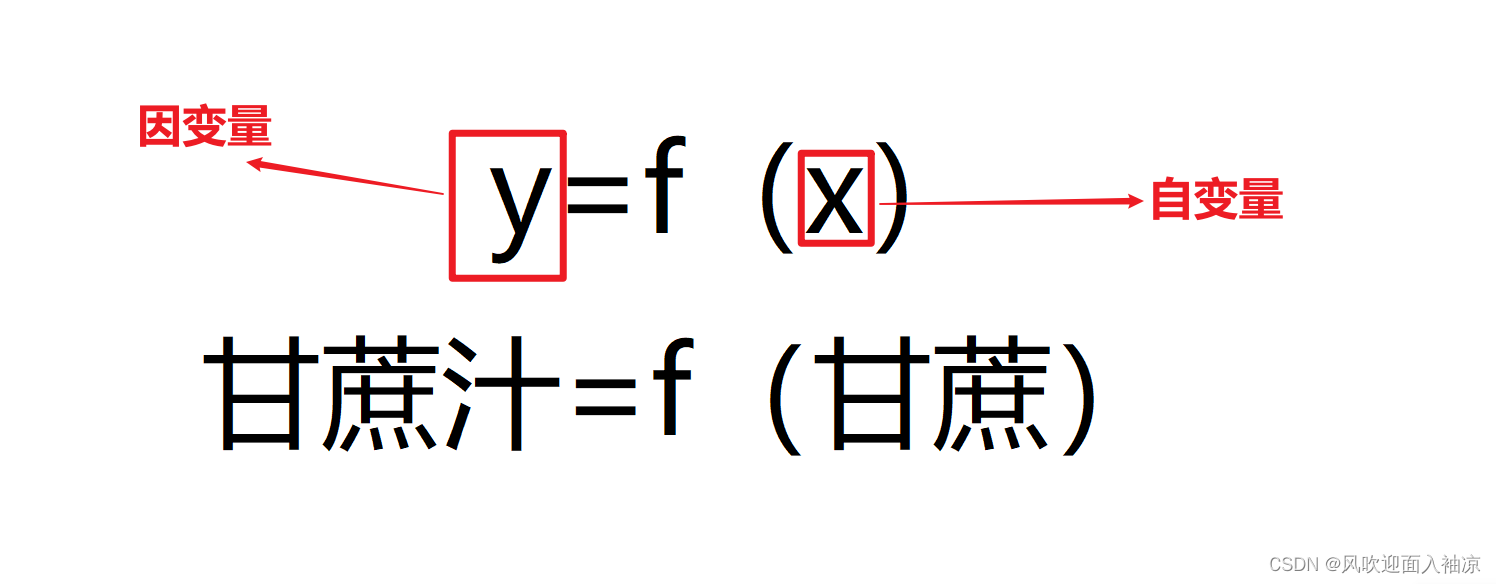
f（）为对应法则，x为甘蔗时，y为甘蔗汁，x为苹果时，y为苹果汁。因为y是随着x的改变而改变的，所以y叫做因变量（因为别人而改变），x叫做自变量（因为自己改变自己）。

概念过一遍即可，如果没理解也不必纠结。

二、什么是定义域

定义域就是咱们x的取值范围，如果咱们把x看成张三，x的取值范围看成是他食量。那么咱们就可以得出：
1.在吃饱的情况下------张三能吃下的饭量为 1
2.在没有吃饭的情况下------张三能吃下的饭量为 3
3.在喝完三大瓶水的情况下------张三能吃下的饭量为 2
简而言之就是在什么的情况下x的取值范围为多少。