第一讲 计算机系统概述
组织与结构
-
组织:不可见(实现结构的具体硬件细节)
- 不直接影响程序执行
- 比如实现乘法是通过单独硬件单元还是重复加法
-
结构:可见(指令集架构,一种抽象属性)
- 直接影响程序逻辑执行的属性
- 比如是否有乘法指令
-
总结:组织是结构的具体实现
组织相同则结构一定相同,结构相同组织不一定相同。
如果遇到题目让你判断,涉及具体实现细节选组织,涉及指令抽象概念结构选结构。
冯诺依曼结构
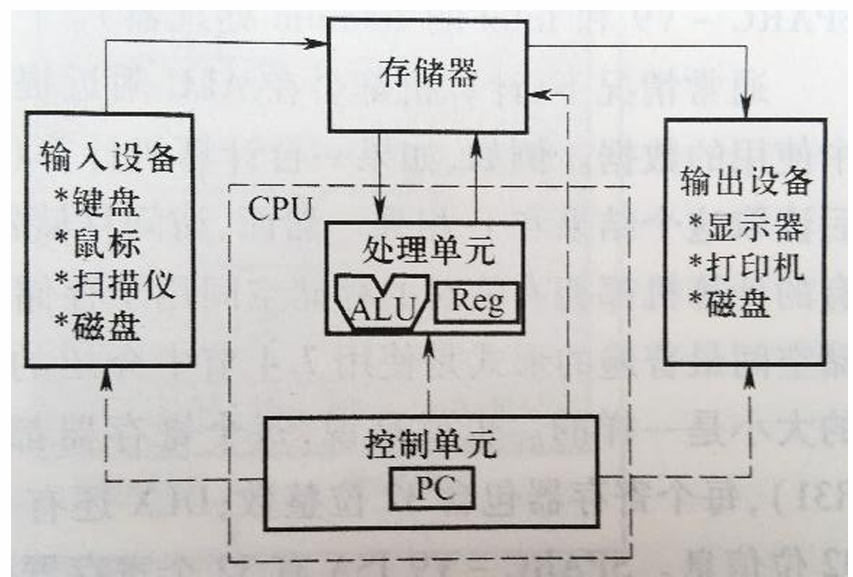
三个原则:
- 计算机由处理单元、存储器、控制单元、输入设备、输出设备组成
- 输入设备将信息送入存储器中,处理单元执行相关运算,输出设备将信息从存储器输出到外界。控制单元负责协调各方运作。
- 指令和数据以同等地位存放在存储器内,并可按地址访问
- 指令和数据均用二进制表示
- 如何区分指令和数据?由CPU的取指-执行周期决定
其中后两条构成了存储程序思想,这是冯诺依曼思想的精髓。
CPU性能(考点!!!)
计算机设计的主要目标是:提高CPU性能。
这里一般会出一题大题。
- 一些概念:
-
时钟频率(速度):CPU在单位时间内执行最基本操作的次数,单位为Hz。
-
时钟周期(周期时间):执行每次最基本操作的时间。
时钟频率 = 1 / 时钟周期 时钟频率 = 1/时钟周期 时钟频率=1/时钟周期 -
C P I i CPI_i CPIi (Cycles Per Instruction)表示指定类型 i i i 所需要的周期数,用 I i I_i Ii 表示在某一给定程序中所执行的 i i i 类指令的条数,则计算整个 CPI 如下:
C P I = ∑ i = 1 n ( C P I i × I i ) I c CPI = \frac{\sum_{i=1}^{n} (CPI_i \times I_i)}{I_c} CPI=Ic∑i=1n(CPIi×Ii) -
执行一个给定程序的处理时间表示为:
T = I c × C P I × t T = I_c \times CPI \times t T=Ic×CPI×t
-
举个简单的例子,
C
P
I
i
CPI_i
CPIi可以用来表示执行一个乘法指令需要多久时间。
C
P
I
CPI
CPI则是执行一个程序每一条指令所需的平均时间,也就是各种指令运行时间的加权平均。
最后的一个程序处理时间的表示其实就是平均每条指令执行的时间乘以指令数。
-
一个关键单位
- 每秒百万条指令(Million Instructions Per Second ,MIPS):
M I P S = I c T × 1 0 6 = f C P I × 1 0 6 MIPS = \frac{I_c}{T \times 10^6} = \frac{f}{CPI \times 10^6} MIPS=T×106Ic=CPI×106f
拆开理解, I c / T I_c/T Ic/T就是总指令数除以程序运行时间,得到的就是每秒能执行多少条指令,再除以10^6就得到每秒能执行多少百万条指令。
- 每秒百万条指令(Million Instructions Per Second ,MIPS):
-
两个平均了解一下,尤其是调和平均记一下

调和平均适合用于平均速率(比如MIPS)
第二讲 数据的机器级表示及检验
整数的补码表示
十进制转二进制补码?
正数:直接转二进制即可
负数:取二进制后取反加一
+5 → 0000 0101
-5 → 1111 1011
怎么转2进制一定要会吧。
二进制补码转十进制?
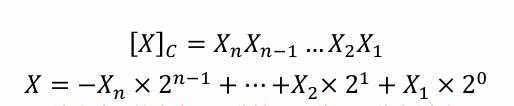
第一位取反,后面和正常二进制转十进制一致。
n位二进制补码的范围:
−
2
n
−
1
<
=
X
<
=
2
n
−
1
−
1
-2^{n - 1} <= X <= 2^{n - 1} - 1
−2n−1<=X<=2n−1−1
浮点数的二进制数表示
- 科学计数法的一般形式为:
± S × B E \pm S \times B^E ±S×BE
其中:
- ±(符号):表示数值的正或负;
- S S S(尾数 / 有效数字,Significand 或 Mantissa):一个规格化的实数,通常满足 1 ≤ S < B 1 \leq S < B 1≤S<B(在二进制中常为 1 ≤ S < 2 1 \leq S < 2 1≤S<2);
- B B B(底 / 基,Base):固定的基数(如十进制中 B = 10 B=10 B=10,二进制浮点中 B = 2 B=2 B=2),对同一系统中所有数相同,无需显式存储(隐含);
- E E E(阶码 / 指数,Exponent):一个整数,可正可负,决定数量级。
具体的IEEE754标准(重点!!!)
规格化的情况:
| 特性 | 单精度 (binary32) | 双精度 (binary64) |
|---|---|---|
| 总位数 | 32 位 | 64 位 |
| 符号位 (S) | 1 位 | 1 位 |
| 指数域 (E) | 8 位 | 11 位 |
| 尾数域 (M / Fraction) | 23 位 | 52 位 |
| 有效数字精度 | ≈ 7 位十进制 | ≈ 15–17 位十进制 |
| 指数偏移量 (Bias) | 127 | 1023 |
| 实际指数范围 | -126 到 +127(规格化) (可表示 ≈ ±10⁻³⁸ 到 ±10³⁸) | -1022 到 +1023 (可表示 ≈ ±10⁻³⁰⁸ 到 ±10³⁰⁸) |
浮点数数值的计算:
( − 1 ) S × ( 1. M ) 2 × 2 E − Bias (-1)^S \times (1.M)_2 \times 2^{E - \text{Bias}} (−1)S×(1.M)2×2E−Bias
特殊情况
- 当阶码
E
=
0
E = 0
E=0 时,表示非规格化数,其值为:
( − 1 ) S × ( 0. M ) 2 × 2 1 − Bias (-1)^S \times (0.M)_2 \times 2^{1 - \text{Bias}} (−1)S×(0.M)2×21−Bias - 当 E 为全 1 E为全1 E为全1时,若M为0表示无穷,若M不为0,表示NaN(Not a Number)
示例(单精度,32 位):
示例 1:将十进制数 +5.0 转换为 IEEE 754 单精度
- 符号位 S:正 →
0 - 二进制表示:
101 - 规格化:
1.01 × 2² - 阶码(Bias = 127):
129 = 10000001 - 尾数:
.01→01000000000000000000000
最终表示:0|10000001|01000000000000000000000
示例 2:将 -0.75 转换为 IEEE 754 单精度
- 符号位 S:负 →
1 - 二进制表示:
0.11 - 规格化:
1.1 × 2⁻¹ - 阶码(Bias = 127):
126 = 01111110 - 尾数:
.1→10000000000000000000000
最终表示:
1|01111110|10000000000000000000000
示例 3:将 IEEE 754 单精度 0 01111110 10000000000000000000000 转回十进制
- 指数:
01111110₂ =126→ 实际指数 =-1 - 尾数:
1.1₂ =1.5 - 值:
1.5 × 2⁻¹ = 0.75
结果:+0.75
浮点数的舍入
只记住向偶数舍入即可(就近舍入)
比如1.0011,只能取三位尾数,1.0011介于1.001和1.010之间,1.010最后一位为偶数,1.001最后一位为奇数。向1.010舍入,注意如果是负数,也一样,先计算出尾数然后舍入。
NBCD(自然BCD码,8421码)
用四位二进制数来表示一个十进制数。
- 符号: 使用四个最高有效位
- 正: 1100 /0
- 负: 1101 /1
- 例子
- +2039:
11000010 0000 0011 1001 /00010 0000 0011 1001 - -1265:
11010001 0010 0110 0101 /10001 0010 0110 0101
- +2039:
纠错(Error Correction)
数据在计算机内部进行计算、存取和传送过程中,由于元器件故障或噪音干扰等原因,会出现差错。因此需要纠错。
- 基本思想
- 存储额外信息进行检错和校正
- 处理过程模板
- 对一段数据生成校验码,放在数据后面,之后需要纠错的时候,根据数据重新生成校验码并于之前的校验码比对。
奇偶校验码
-
假设数据为 𝐷 = 𝐷 𝑀 … 𝐷 2 𝐷 1 𝐷=𝐷_𝑀…𝐷_2𝐷_1 D=DM…D2D1
-
数据输入
- 奇校验: 𝐶 ′ = 𝐷 𝑀 ⊕ ⋯ ⊕ 𝐷 2 ⊕ 𝐷 1 ⊕ 1 𝐶'=𝐷_𝑀⊕⋯⊕𝐷_2⊕𝐷_1⊕1 C′=DM⊕⋯⊕D2⊕D1⊕1
- 偶校验: 𝐶 ′ = 𝐷 𝑀 ⊕ ⋯ ⊕ 𝐷 2 ⊕ 𝐷 1 𝐶'=𝐷_𝑀⊕⋯⊕𝐷_2⊕𝐷_1 C′=DM⊕⋯⊕D2⊕D1
-
数据输出
- 奇校验: 𝐶 ′ ′ = 𝐷 𝑀 ′ ⊕ ⋯ ⊕ 𝐷 2 ′ ⊕ 𝐷 1 ′ ⊕ 1 𝐶''=𝐷'_𝑀⊕⋯⊕𝐷'_2⊕𝐷'_1⊕1 C′′=DM′⊕⋯⊕D2′⊕D1′⊕1
- 偶校验: 𝐶 ′ ′ = 𝐷 𝑀 ′ ⊕ ⋯ ⊕ 𝐷 2 ′ ⊕ 𝐷 1 ′ 𝐶''=𝐷'_𝑀⊕⋯⊕𝐷'_2⊕𝐷'_1 C′′=DM′⊕⋯⊕D2′⊕D1′
为什么叫奇偶校验?奇(偶)校验码的校验结果C为0则表示数据种的1的数目为奇数(偶数)
最后比对两次的校验码是否相同,相同则未出错,或者偶数个出错。不同则偶数个出错。
海明码
- 基本思想:将数据分成几组,对每一组都使用奇偶校验码进行检错。
设原始数据有 m 位,需添加 r 个校验位,则:
一定需要满足
2
r
>
=
m
+
r
+
1
2^r >= m + r + 1
2r>=m+r+1
校验位(P) 放在 2 的幂次位置:1, 2, 4, 8, 16,等等(注意从1开始标号),数据位(D) 放在其余位置。
将位置编号写成二进制,Pᵢ 对应第 i 位(从1开始),Pᵢ 覆盖所有位置编号的二进制中第 i 位为 1 的位**(包括自己)**。Pi对覆盖的位进行偶检验。
最后对传输得到的代海明码的结果再进行计算一次相同覆盖的偶检验。得到故障字故障字的值就代表是哪位数字出错了,若全零则代表没有错误。
举个例子:
原始数据:1011(D₁=1, D₂=0, D₃=1, D₄=1)
4 + 3 + 1 = 2^3,因此3位校验位即可。
1. 安排位置(P=校验位,D=数据位):
| 位号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 类型 | P₁ | P₂ | D₁ | P₃ | D₂ | D₃ | D₄ |
| 值 | ? | ? | 1 | ? | 0 | 1 | 1 |
2. 计算校验位(使覆盖位中“1”的个数为偶数):
- P₁ 覆盖 1,3,5,7 →
? ⊕ 1 ⊕ 0 ⊕ 1 = 0→ P₁ = 0 - P₂ 覆盖 2,3,6,7 →
? ⊕ 1 ⊕ 1 ⊕ 1 = 0→ P₂ = 1 - P₃ 覆盖 4,5,6,7 →
? ⊕ 0 ⊕ 1 ⊕ 1 = 0→ P₃ = 0
编码结果:0 1 1 0 0 1 1
假设接收时第 5 位出错 → 收到:0 1 1 0 1 1 1
3. 计算故障字(Syndrome):
- S₁ = 0⊕1⊕1⊕1 = 1
- S₂ = 1⊕1⊕1⊕1 = 0
- S₃ = 0⊕1⊕1⊕1 = 1
→ Syndrome = (S₃S₂S₁)₂ = 101₂ = 5
4. 纠错:翻转第 5 位 → 恢复为 0 1 1 0 0 1 1
最后注意一点海明码默认只会有一位数字出错。
循环冗余检验
- 基本思想
- 假设数据有M位,左移数据K位(右侧补0),并用K+1位生成多项式除它**(模2除法)**
- 采用K位余数作为校验码
- 把校验码放在数据(不含补的0)后面,一同存储或传输
- 校错
- 如果M+K位内容可以被生成多项式除尽,则没有检测到错误
- 否则,发生错误
必须一下这个原始数据位100011,生成多项式位1001的例子
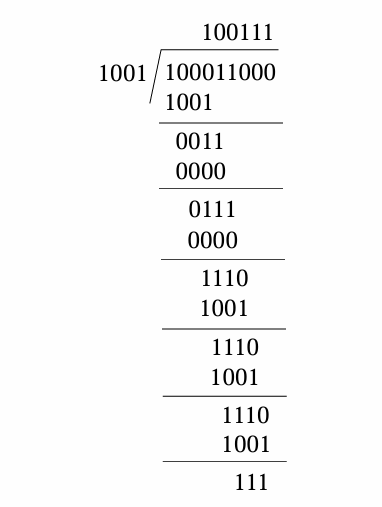
第三讲 整数运算
算术逻辑单元 (ALU) 是计算机实际完成数据算术逻辑运算的部件
数据由寄存器提供给ALU,结果也储存在寄存器中
控制单元 (Control unit) 提供控制ALU操作和数据传入送出ALU的信号
ALU可能根据运算结果设置一些标志 (Flags),标志值也保存在处理器内的寄存器中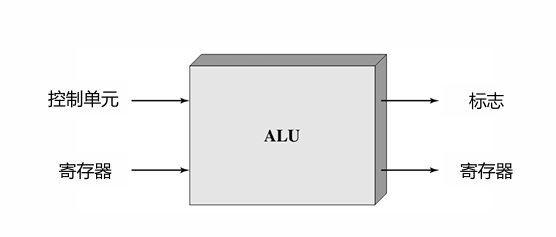
全加器
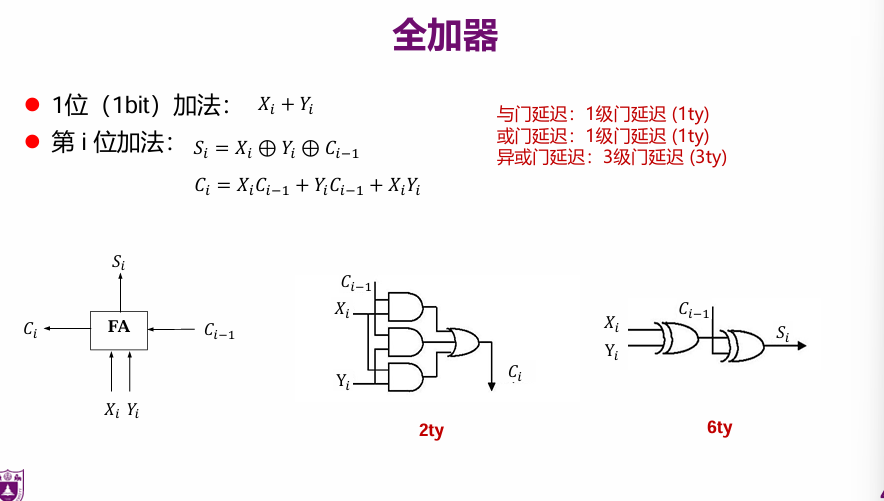
注意这里的延迟是人为定义的,考试的时候看清楚。总的延迟看耗时最长的那条路。
串行进位加法器
S表示这一位 的结果,C表示进位
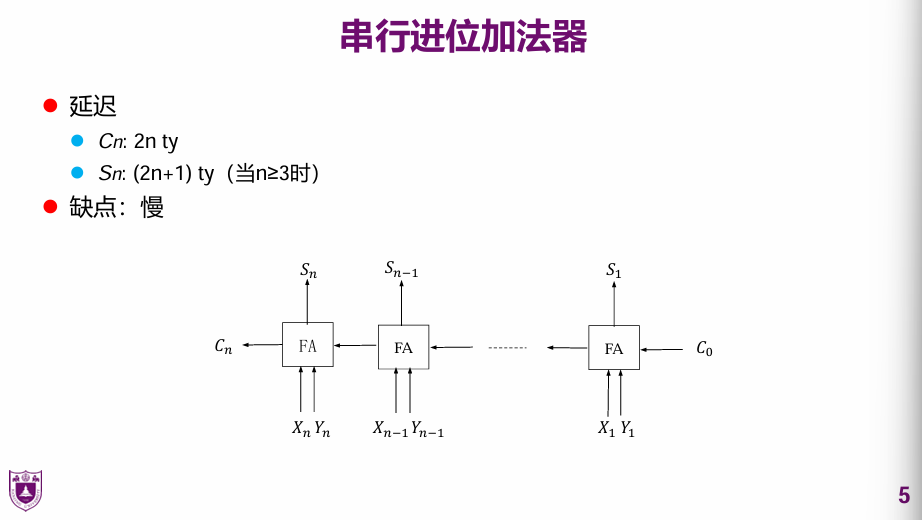
注意可以进行并行运算,所以Sn != 6n.
全先行进位加法器
串行进位加法器慢就慢在需要等前一位计算得出进位才能进行这一位的运算。但是进位是可以提前得出的,具体推导如下:

P和G的计算需要一个周期,C需要两个周期,最后S在需要3周期(别忘了X,Y的异或以及并行完成了)
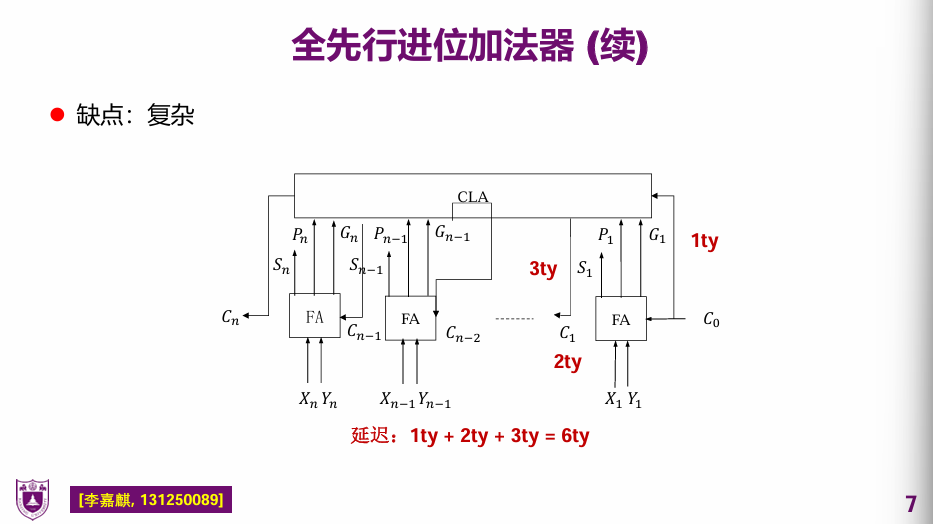
部分先行进位加法器
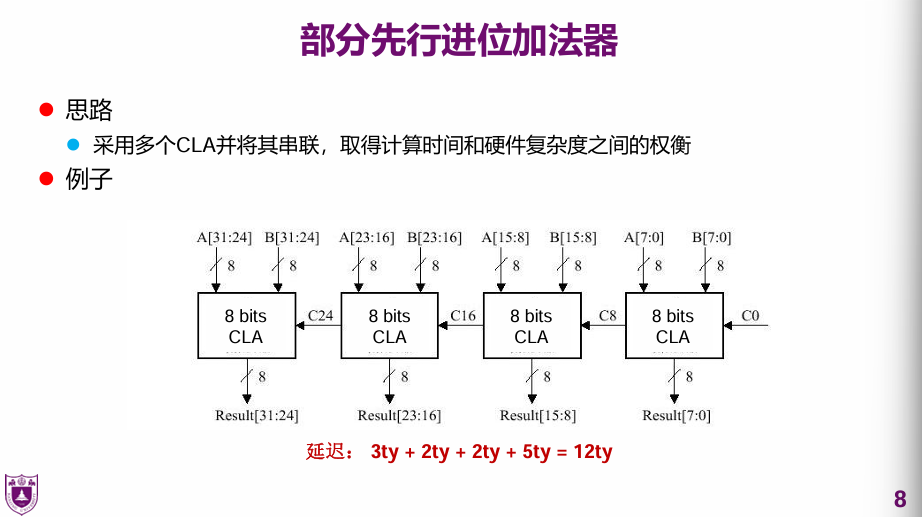
建议直接死记硬背这个公式。3是最开始的,5是最后的。
加法
注意一点,溢出直接舍去前面的那一位,位数允许则直接保留(不要管变符号)

减法
对减数取反加一即可。

布斯乘法
牢牢记住布斯乘法即可。
𝑋×𝑌=𝑋×𝑌𝑛𝑌𝑛−1…𝑌2𝑌1
- 增加Y0= 0
- 根据Yi+1Yi, 决定是否增加 +X, -X, +0(看Yi - Yi + 1)
- 右移部分积(算数右移)
- 重复步骤2和步骤 3共n 次,得到最终结果
例子:

注意一下,是加在前四位。
除法
首先是四种特殊情况
- 若被除数为0,除数不为0:商为0
- 若被除数不为0,除数为0:发生“除数为0”异常
- 若被除数、除数均为0:发生“除法错”异常
- 若被除数、除数均不为0:进行进一步除法运算
具体步骤
- 通过在前面加n位符号扩展被除数,并存储在余数寄存器和商寄存器中
- 将余数和商左移,判断是否“够减”(余做减法或加法后不变号)
- 如果“够”,则做减法(同号)或者加法(异号),并上商为1
- 如果“不够,则上商为0
- 重复以上步骤
- 如果除数和被除数不同号,则将商替换为其相反数
- 余数存在余数寄存器中
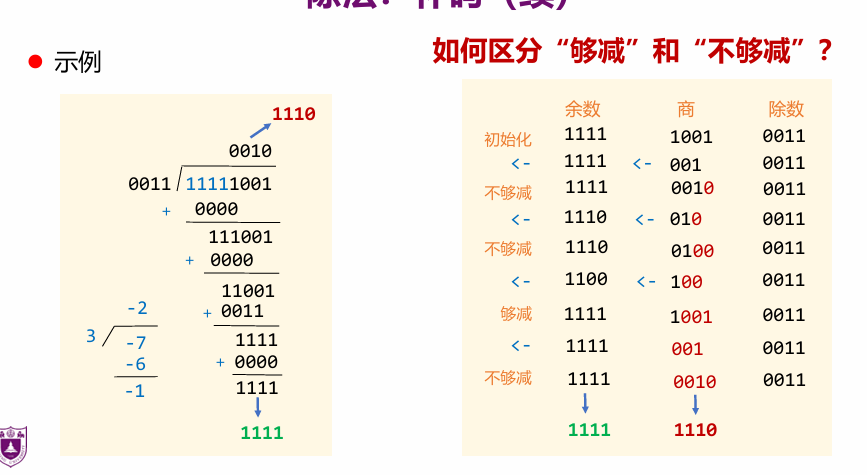
恢复余数除法:试着减,不够则恢复。
不恢复余数除法:硬着头皮上。(不要求)
个人网站:https://panjiebin13.github.io/my-blog/
文中图片来自南京大学计算机组织结构2025年秋季课程PPT






















 995
995

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








