第6章：关于二分搜索树的那些事（1）

第六章 二分搜索树

6-1 为什么要研究树结构
6-2 二分搜索树基础
6-3 向二分搜索树中添加元素
6-4 改进添加操作：深入理解递归终止条件
6-5 二分搜索树的查询操作
6-6 二分搜索树的前序遍历
6-7 二分搜索树的中序遍历和后序遍历

---

6-1 为什么要研究树结构

1. 树结构本身是一种天然的组织结构，如：文件目录结构，图书馆图书索引，公司的组织架构etc.
2. 树结构存储数据的优点：高效
3. 树结构主要分为以下几类：
   二分搜索树(Binary Search Tree)；平衡二叉树；AVL；红黑树；堆；并查集；线段树；Tier(字典树，前缀树)

6-2 二分搜索树基础

1. 二叉树的定义：
   和链表一样，二叉树是动态数据结构
   
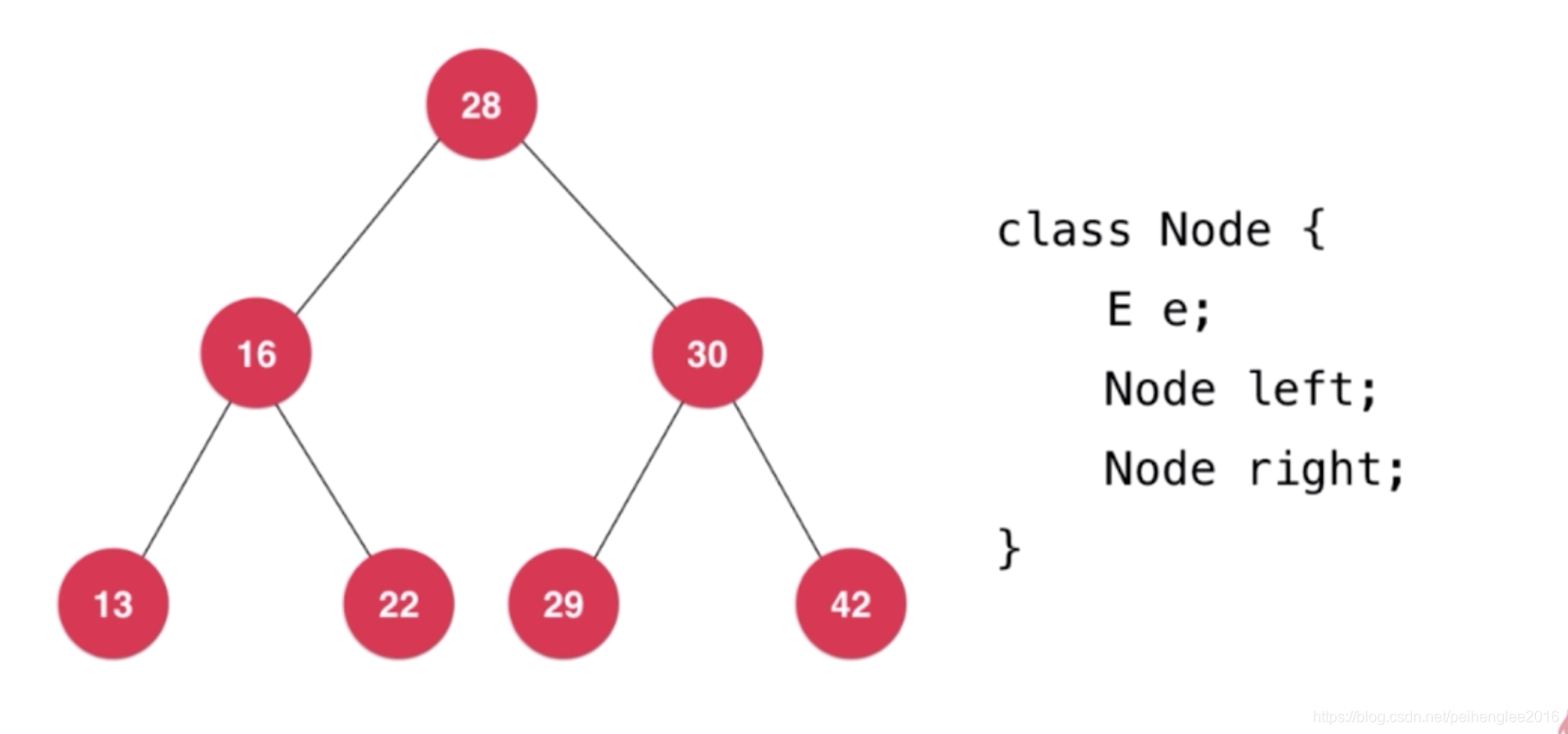
   二叉树具有唯一根节点，每个节点最多有两个孩子(左孩子，右孩子)，没有孩子的节点称作叶子节点。每个节点最多有一个父亲。
   
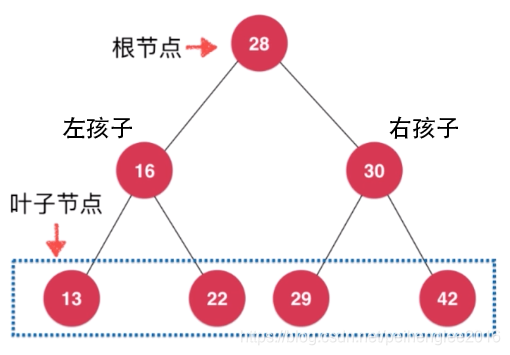
   二叉树具有天然递归结构：每个节点的左子树也是二叉树， 每个节点的右子树也是二叉树
   
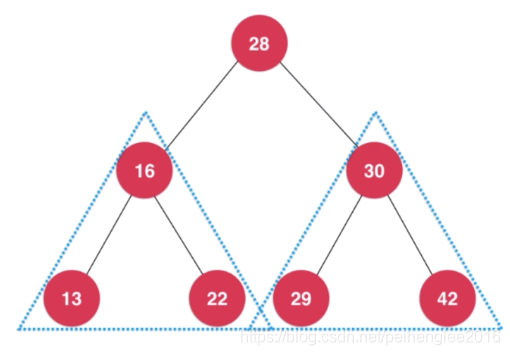
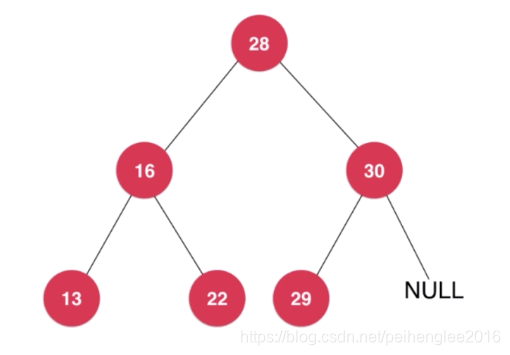
   二叉树不一定是“满”的：一个节点也是二叉树，NULL 空也是二叉树
   

2. 二分搜索树的定义：
   二分搜索树是二叉树
   二分搜索树的每个节点的值：大于其左子树的所有节点的值，小于其右子树的所有节点的值
   每一棵子树也是二分搜索树
   存储的元素必须具有可比较性(举个栗子：数据之间具有可比较性)

3. 简单的二分搜索树代码实现：

public class BTS<E extends  Comparable<E>> {
    private class Node{
        public E e;
        public Node left, right;

        public Node(E e){
            this.e = e;
            left = null;
            right = null;
        }
    }
    private Node root;
    private int size;

    public BTS(){
        root = null;
        size = 0;
    }
    public int size(){
        return size;
    }
    public boolean isEmpty(){
        return size == 0;
    }
}

6-3 向二分搜索树中添加元素

• 我们的二分搜索树不包含重复元素
  1.如果想包含重复元素的话，只需要定义：左子树小于等于节点；或者右子树大于等于节点
  2.注意：我们之前讲的数组和链表，可以有重复元素

• 二分搜索树添加元素的非递归写法，和链表很像
  1.二分搜索树在最坏的情况下会退化一个链表，此时递归就可能会有更多的开销
  2.在二分搜索树方面，递归比非递归实现简单

• 简单的代码实现二分搜索树中添加新的元素

// 向二分搜索树中添加新的元素e
    public void add(E e){
        if (root == null){
            root = new Node(e);
            size ++;
        }
        else
            add(root, e);
    }
// 向以node为根的二分搜索树中插入元素E，递归算法
    private void add(Node node, E e){
        if (e.equals(node.e))
            return;
        else if (e.compareTo(node.e) < 0 && node.left == null){
            node.left = new Node(e);
            size ++;
            return;
        }
        else if (e.compareTo(node.e) > 0 && node.right == null){
            node.right = new Node(e);
            size ++;
            return;
        }
        
        if (e.compareTo(node.e) < 0)
            add(node.left, e);
        else // e.compareTo(node.e) > 0
            add(node.right, e);
    }
}

6-4 改进添加操作：深入理解递归终止条件

• 当前出入操作存在的问题：
  1.首先，理解递归操作，向以node为根的二分搜索树添加元素e，其实我们是把元素e插入到node的左孩子或者右孩子。其次，public的那个方法，对根节点做了特殊处理，这样就形成了逻辑上的不统一。
  2.另外，这个递归算法对e和node.e进行了两轮比较：其实null也是一个二叉树，当我们走到了null的二叉树就一定要插入一个节点，但是我们做到这里没有把二叉树给挂接起来（需要返回给上层）

• 递归实现技巧：
  1.把一个问题化成n个相同的基础问题
  2.比如向二分搜索树中添加元素这个问题，用递归的思想来考虑的话，把每个二分搜索树中的一个根节点和两个子节点当成基础问题（其实就是向一个三角形的树中插入元素的问题，用函数进行实现。

   // 向二分搜索树中添加新的元素e
    public void add(E e){
        root = add(root, e);
    }
    
    // 向以node为根的二分搜索树中插入元素e，递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e){
        if (node == null){
            size ++;
            return new Node(e);
        }
        
        if (e.compareTo(node.e) < 0)
            node.left = add(node.left, e);
        else if (e.compareTo(node.e) > 0)
            node.right = add(node.right, e);

        return node;
    }

6-5 二分搜索树的查询操作

• 二分搜索树中的查询操作： 只需要查看每个节点是否包含该元素即可；而不需要在递归算法中将元素挂接上一运算过程中。
  --------> 之后可以尝试实现非递归算法的代码实现
• 由于二分搜索树本身并没有索引的概念，因此在修改节点元素的方法有所不同。

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e){
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e，递归算法
    private boolean contains(Node node, E e){
        if (node == null)
            return false;

        if (e.compareTo(node.e) == 0)
            return true;
        else if (e.compareTo(node.e) < 0)
            return contains(node.left, e);
        else // e.compareTo(node.e) > 0
            return contains(node.right, e);
    }

6-6 二分搜索树的遍历

• 遍历操作就是把所有节点都访问一遍；
  访问的原因和业务相关；
  在线性结构下，遍历是极其容易的；相反，树结构中的遍历操作较难（也没那么难：）

• 二分搜索树中递归与遍历的区别：
  递归：从根节点开始，来看根节点元素是否是我们要查找/添加的元素，如果是直接执行操作，如果不是，看查找/添加的元素是否小于根节点，小于根节点就在左子树中继续进行操作；大于根节点就在右子树中继续进行操作。换句话说，在递归的过程中，我们每次只选择一个子树进行操作，直到达到递归的终止条件。
  遍历：对于遍历来说，两棵子树都要顾及（左子树一次，右子树一次，相当于进行了两次递归的调用）

• 二分搜索树的遍历包括：前序遍历，中序遍历和后序遍历。
  前序遍历：先访问节点，再访问左右子树

function traverse (node):
if(node == null)
return;

前序遍历：
step1: 访问该节点
step2: traverse(node.left)
step3: traverse(node.right)

前序遍历简单的代码实现：

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }
    // 前序遍历以node为根的二分搜索树，递归算法
    private void preOrder(Node node){
        if (node == null)
            return;
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

public class Main {
    public static void main(String[] args) {
        BTS<Integer> bts = new BTS<>();
        int [] nums = {5, 3, 6, 8, 4, 2};
        for (int num: nums)
            bts.add(num);
        bts.preOrder();
        System.out.println();
    }
}

结果如下：

////////////////////////////
// 5 //
// / \ //
// 3 6 //
// / \ \ //
// 2 4 8 //
////////////////////////////

二分搜索树前序遍历的toString方法中，展现形式可以是先展现根节点，再展现左子树，接着展现右子树
二分搜索树打印输出时可以使用“层序遍历”来打印出树形结构图。

@Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBTSString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBTSString(Node node, int depth, StringBuilder res){
        if (node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }
        res.append(generateDepthString(depth) + node.e + "\n");
        generateBTSString(node.left, depth+1, res);
        generateBTSString(node.right, depth+1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for (int i = 0; i < depth; i ++)
            res.append("--");
        return res.toString();
    }
}

System.out.println(bts);

打印出来的结果如下：

5
–3
----2
------null
------null
----4
------null
------null
–6
----null
----8
------null
------null

6-7 二分搜索树的中序遍历和后序遍历

重点：树结构的遍历方式分为：前序遍历，中序遍历和后序遍历：

1. 前序遍历：先访问节点，再访问节点的左子树，最后访问右子树（最常用的遍历方式）
2. 中序遍历：先访问节点的左子树，再访问节点，最后访问右子树（二分搜索树的中序遍历结果是顺序的）
3. 后序遍历：先访问节点的左子树，再访问右子树，最后访问节点（后序遍历的应用：为二分搜索树释放内存）
   —> 释放一个节点需要先释放它的子树，java由于存在垃圾自动回收机制，因此不需要考虑这个。

中序遍历简单的代码实现：

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }
    // 中序遍历以node为根的二分搜索树，递归算法
    private  void inOrder(Node node){
        if (node == null)
            return;
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

function traverse (node):
if(node == null)
return;

中序遍历：
step1: traverse(node.left)
step2: 访问该节点
step3: traverse(node.right)

后序遍历简单的代码实现：

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }
    // 后序遍历以node为根的二分搜索树，递归算法
    private  void postOrder(Node node){
        if (node == null)
            return;
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

function traverse (node):
if(node == null)
return;

后序遍历：
step1: traverse(node.left)
step2: traverse(node.right)
step3: 访问该节点

下面我们将这三种遍历方法在Main函数中进行比较；

        // 前序遍历
        bts.preOrder();
        System.out.println();
        // 中序遍历
        bts.inOrder();
        System.out.println();
        // 后序遍历
        bts.postOrder();
        System.out.println();

运行结果如下：

前序遍历： 5 -> 3 -> 2 -> 4 -> 6 -> 8
中序遍历： 2 -> 3 -> 4 -> 5 -> 6 -> 8
后序遍历： 2 -> 4 -> 3 -> 8 -> 6 -> 5