参数多项式曲线
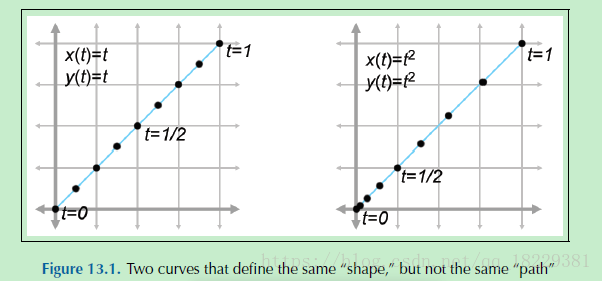
参数曲线
x(t) = cos(2*Pi*t)
p(t)= (x(t), y(t))
多项式曲线
多项式参数曲线是参数 曲线方程能够写成多项式形式
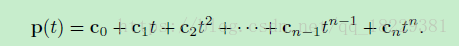
矩阵符号
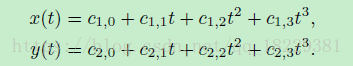
矩阵形式
线段和点

单项式形式的端点
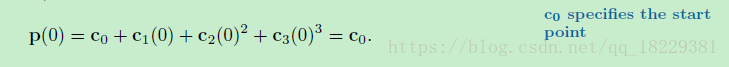
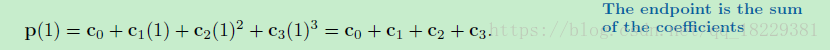
速度和切线
曲线可以是静态,也可以是动态。静态:形状,动态:物体随时间运动的轨迹。
动态:即时速度?速度变化?
v(t)是p(t)的一阶导数
a(t)是p(t)的二阶导数
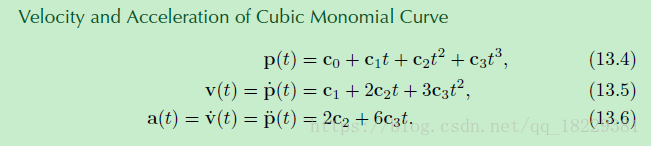
曲线重参数化
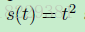
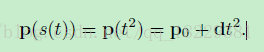
切线

二阶导数和曲率有关,曲率k = 1/r,r为半径。直线段曲率为0,可以看成是半径无穷大的圆的曲率。
曲率计算公式:
多项式插值
线性插值
多项式的度决定于控制节点个数,n度的多项式用来插值n+1个控制点。比如线段是一度的多项式插值。
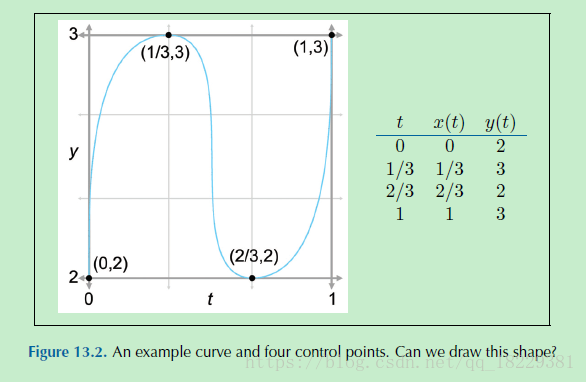
Aitken’s Algorithm
“分而治之”,创建一个对n个控制节点进行插值的曲线,将这个曲线分为两个简单的曲线:(1)只对前n-1个点插值,不管最后一个点;(2)只对最后n-1个点插值,不管第一个。然后将两条曲线混合。
4个控制点,对应4个时间,我们先分为两个小问题:前3个点和 最后一个点,前一个点和最后3个点。3个控制节点构造2度的曲线,还是比较复杂。我们再次拆分,前两个点和最后一个点,第一个点和最后两个点。这两条曲线都只有两个控制点,是线段。
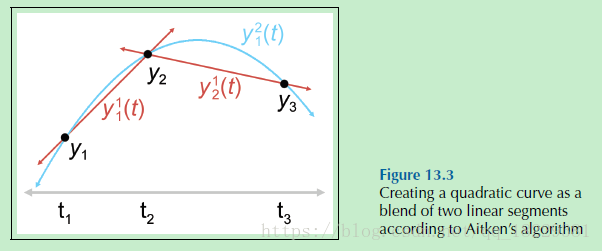
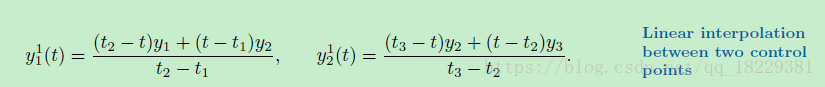
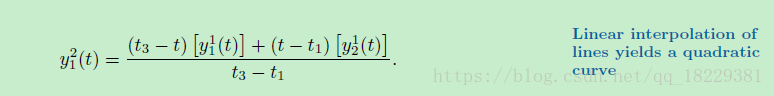
你能看出来这种模式:每种曲线都是比他小一阶(度)的曲线的线性插值得到的。
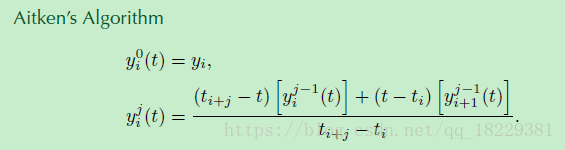
Aitken算法中,被融合的两个曲线都径功中间控制点,两边的控制点被其中一个曲线经过。
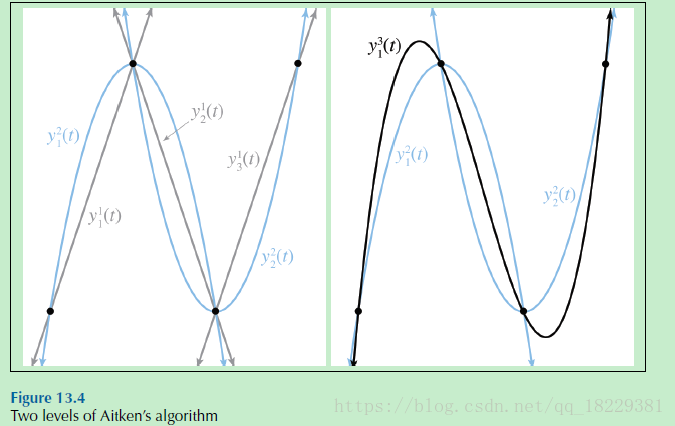
但是,尽管上面的曲线经过了4个控制点,但并不是我们想要的曲线,如下所示,一个s型曲线。
我们看到Aitken算法生成的曲线的y值超过了两个中间控制点的y值。
我们得到了一个事实:
多项式插值无法让我们控制几何设置里的曲线设计。
但是,不要失望,我们也学到了几个重要的,在讨论bezier曲线的时候的思想。
Aitken算法是一个将曲线混合的递归算法,通过不断的线性插值得到。
拉格朗日基础多项式
我们从抽象的数学角度看这个问题。每一个控制节点能得到一个等式,每一个多项式系数是一个未知数。这一系列等式组成一个n*n矩阵,能通过一些方法得到解。
解一个n*n的矩阵,需要O(n3)时间。很幸运,有简单方法。像Aitken算法一样,分解为更小的问题,然后将结果混合。Aitken算法是一个递归算法,而这里,我们对每个控制点用一个更简单的问题。我们不管y,只考虑t。我们创建一个多项式,对每个t,多项式在该节点的值都是1,而其他节点都是0.如果我们把第i个多项式表示为Li,那么这个方法可以写为:Li(ti)=1,Li(tj)=0(j!=i)。比如n=4,那我们在节点处有以下等式:
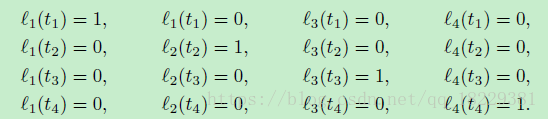
如果我们用上面的属性创建多项式,那么我们可以把他们用作基础多项式。我们将每个基础多项式Li放大相应的坐标值倍(Yi倍),然后将所有放大倍数后的多项式加到一起:
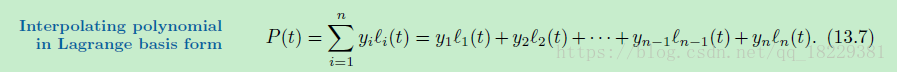
注意,这个基础多项式只依赖于关节向量(t),而不是坐标值(y)。这样,一系列基础多项式可以被用来快速创建很多曲线(用相同的关节向量)。这些3d曲线有相同的关节序列。
所有的关键是我们要知道基础多项式, 然后我们发现Li是多项式混合的一个关键问题。然而我们想让插值的数据点在0和1之间。所以Li可以用一种简单的方式表示,拉格朗日基础多项式Li像下面一样:
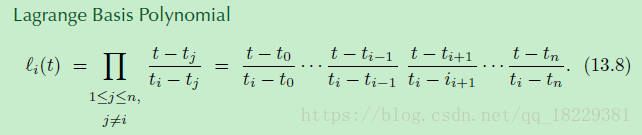
这个小技巧能够成功,在于,对于节点ti,惩罚中的所有项都是1,乘法为1.在任意其他节点,其中有一项为0,导致乘法结果为0.
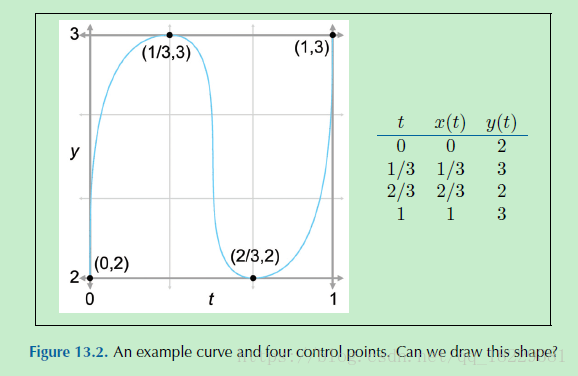
我们将这个用到我们的S曲线上。该曲线的关节点是(0, 1/3, 2/3, 1).这里我们计算第一个基础多项式:
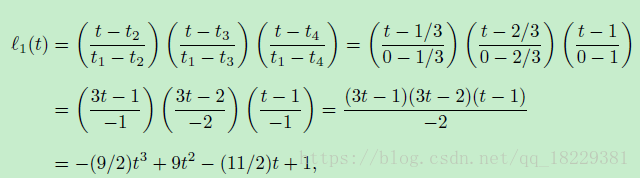
我们得到了关节向量的拉格朗日基础多项式,我们把y值也放到方程里面,得到完整的插值多项式:
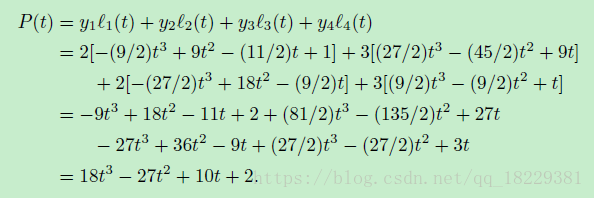
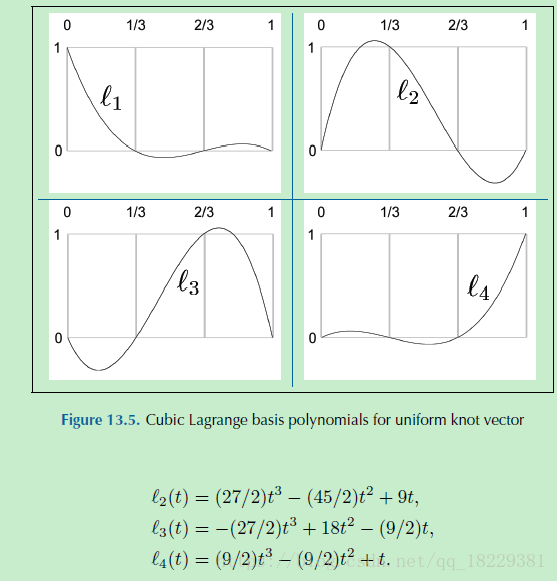
我们用图像方式看一下这个问题,首先将每个基础多项式乘以相应的坐标:
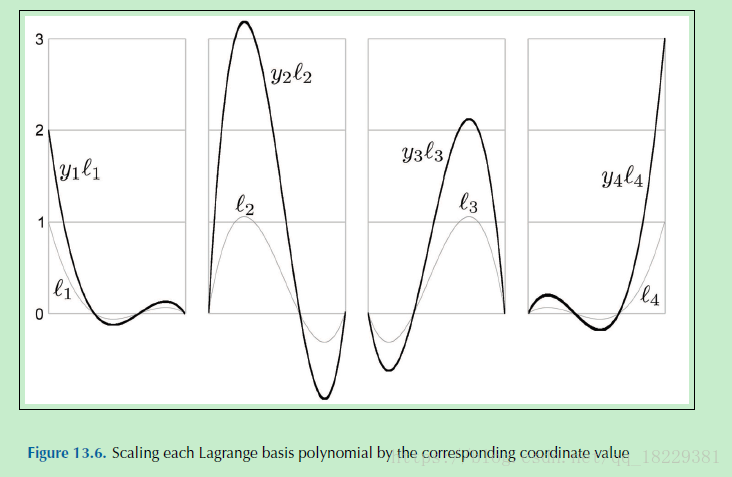
插值曲线
控制点像建筑的转发,基础多项式提供了scale参数,我们更喜欢把这些点叫做重心坐标。
一些值是负数或者大于1,所以游戏多项式直接插值会超出控制点。当所有的重心的坐标在(0,1)范围内,得到的点在控制点的凸包内。就像你在控制点周围拉橡皮筋一样。但我们只要有任意一个坐标超出(0,1),得到的点就会在凸包外。几何曲线设计中,保证在凸包内比较好。第4部分的bezier曲线就会有这种保证,通过Bernsterin 基数来达到。
多项式插值总结
两张方式看多项式插值:Aitken算法基于重复线性插值,拉格朗日通过创建基础方程,依赖于关节向量进行插值。
n度多项式有n+1度自由变量,对应单项式的n+1个系数,所以n度多项式插值n+1个控制点是唯一的。线性代数唯一解的问题类似。
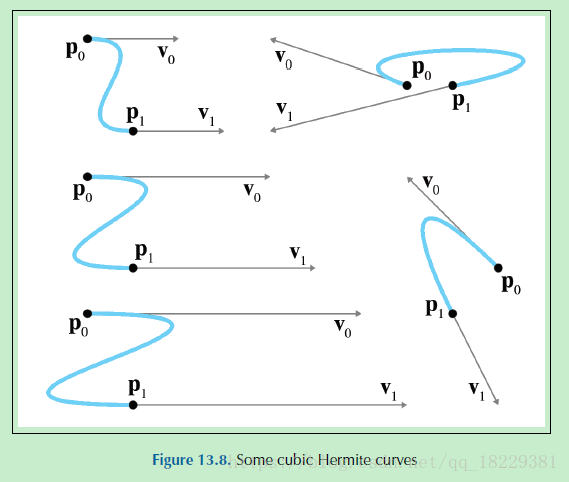
Hermite形式(端点和导数)
通过多项式插值控制曲线内部(曲线穿过特定的节点),有时候效果不太好,由于有时候会超出或者摆动,我们尝试另一种方式。当然仍然要指定端点坐标,但,不再知道内部插值点的坐标,儿是通过控制端点的切线来控制曲线的形状。这种曲线称为Hermite曲线或者Hermite形式的曲线。
Hermite形式指定一个曲线通过列出其开始和结束坐标及导数。立方体曲线只有4个系数,能指定端点处的一阶导数,端点处的速度。所以Hermite形式描述一个立方体曲线有以下四种信息:
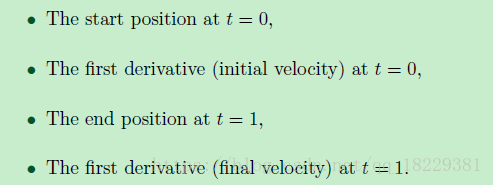
开始节点叫做P0,终止节点叫P1,开始速度v0,结束速度v1.
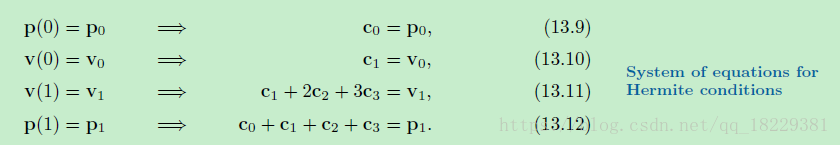
单项式

矩阵形式
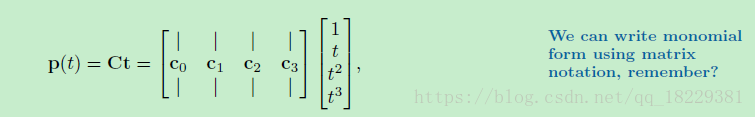
立方Hermite曲线
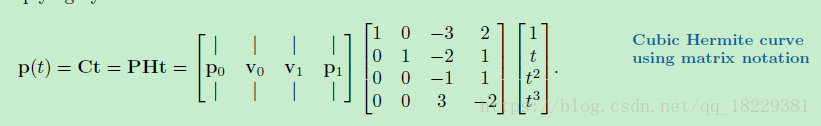
Hermite基础

立方Heremite基础方程

基础方程作为混合权重
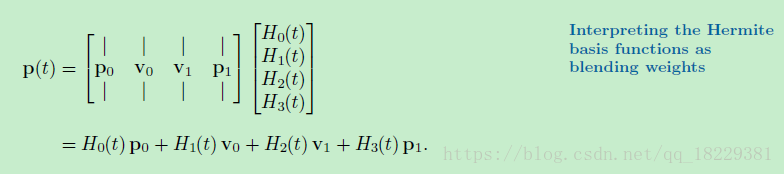
图像
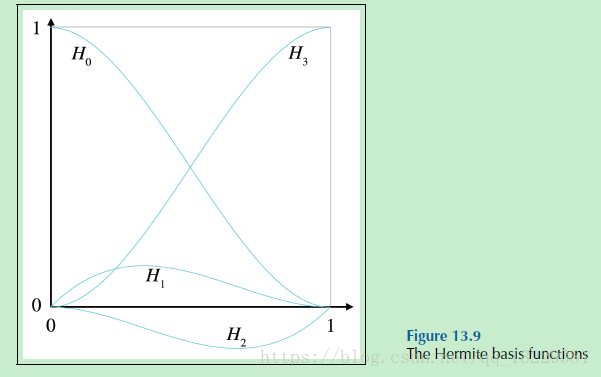
H3(t)是光滑方程。hlsl里面会发现。更简单点,我们用正常的插值小数t,然后把t替换成H3(t),就会光滑。这是因为光滑方程使端点处的速度突变消除。
指定加速度a,能得到5阶Hermite曲线。
Bezier形式(端点、控制点)
Bezier曲线近似而不是插值:尽管Bezier曲线穿过第一个和最后一个端点,他只是经过中间的点。所以Bezier里的点称为控制点,而不是关节点。上面说了,多项式插值问题有两种解决方法:Aitken的递归算法,拉格朗日基础多项式算法。Bezier曲线有相同的二元性。Bezier曲线中Aitken算法对应算法是德卡斯特里奥算法,通过递归算法重复线性插值构建Bezier曲线。与拉格朗日基础方程对应的是Bernstein基础。还讲了Bezier曲线的导数,揭示了和Hermite形式的关系。
Bezier曲线中,几何和代数之间的合作如此优雅。
de Casteljau算法
应用在立方曲线上:
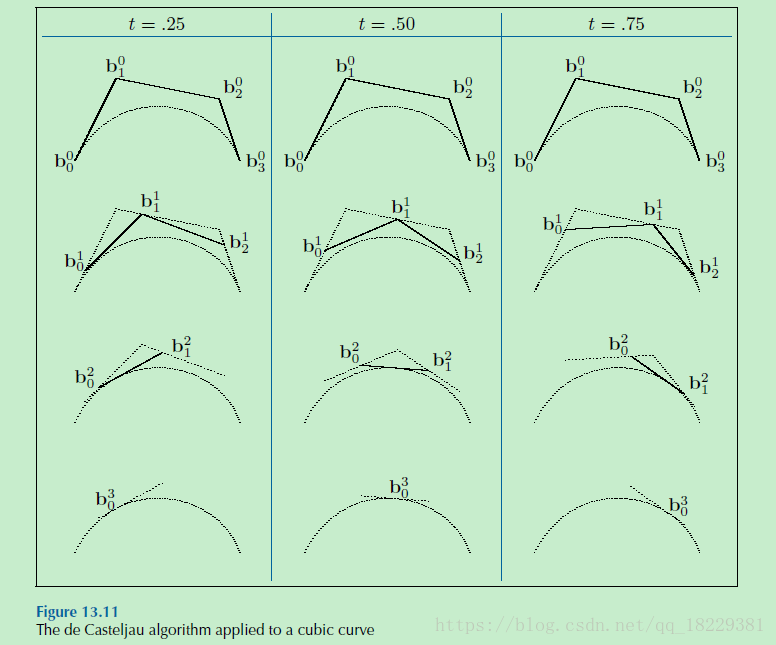
可以将所有的b写成三角形的形式:
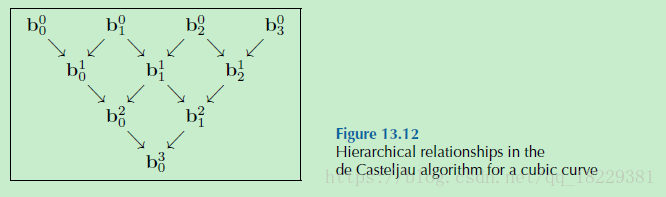
将基础线性插值公式和递归关系相结合就得到了de Casteljau递归关系
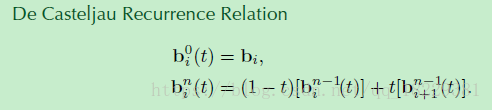
这能通过不断的插值,将一个点放在任意t的位置,但并不能通过控制节点给大家一个封闭的表达形式。
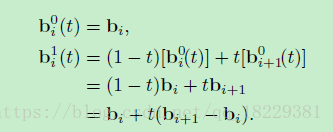
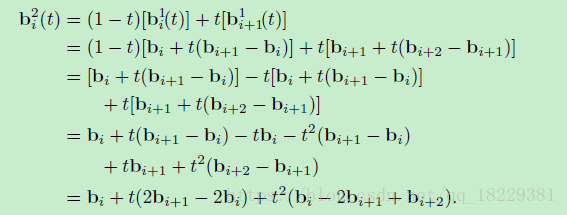
也就是说平方Bezier曲线,有3个控制节点,可以用以下的单项式形式表示:
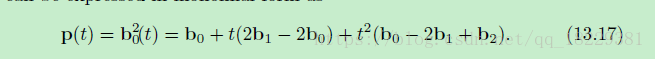
矩阵形式:
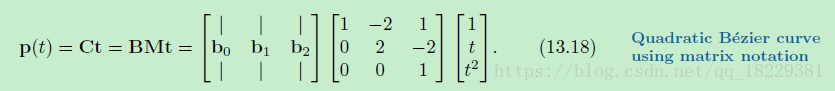
Bernstein基数
通过Bezier控制点计算曲线多项式,上面已经有了其单项式形式,系数是t的幂。我们也可以写成控制节点的形式而不是时间的形式。这样写,每个控制节点都有一个系数,这个系数是t的函数,代表了该控制节点贡献给曲线的重心权重。
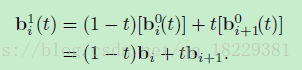
平方形式
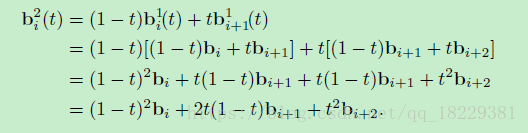
立方形式
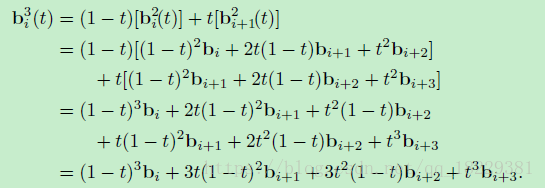
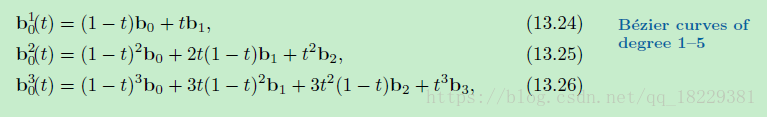
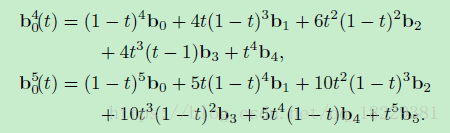
我们能够看出每一项有一个特定的系数,1-t的幂和t的幂。t的指数递增,1-t的指数相反,递减。
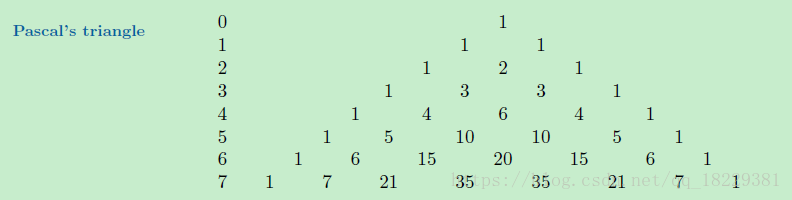
每个数都是他上面两个数的和。这个数字形式是二项式系数。第n行是二项式(a+b)的n次方展开的系数。这个二项式系数的三角形排列被称为pascal三角形。
二项式系数有一个特殊的表示

读做n选k,因为它正好是从n个数中选出k个数的子集数(无序排列)。计算二项式系数的一般公式

其中用到阶乘,0的阶乘是1.排列和组合中用到二项式系数比较多,比如概率和算法分析。
回到曲线,我们分析了重心权重的形式,现在我们重写bezier曲线,将每个控制节点的权重用二项式系数表示。
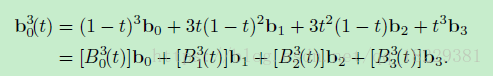

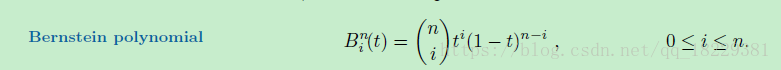
Bernstein多项式的属性
1. 对于任意t,和都为1;
2. 凸包属性:曲线在控制节点的凸包范围内;
3. 端点插入,第一个和最后一个多项式达到1;
4. 全局支持:所有的多项式在(0,1)范围内都是非0,一个控制节点的混合权重非0,称为控制节点的支持。不论何时,控制节点支持,他对曲线发挥了影响。Bezier控制节点有全局支持,因为Bernstein多项式除了端点,在其他地方都是非0.实践结果就是移除任意一个控制节点,整个曲线都会受到影响。而如果移除一个节点后,只有控制节点附件的局部曲线会受到影响,说明是局部支持。局部支持意味着,基础函数只在部分区间是非0的,在这个区间外是0.不幸的是,这种基础函数不能被称为多项式,所以没有多项式曲线能达到局部控制。然后,将小的曲线组合到一起可以形成一个样条曲线。
5. 局部最大。尽管每个控制节点对整个曲线都有影响,每个控制节点在曲线上特定的点影响最大。每个Bernstein多项式Bin(t)都是控制点Bi的混合权重,在t=i/n的时候最大。另外,在那个时候,bi比任意其他控制点的影响都大。所以,尽管曲线上的每个点都对曲线有影响,最近的控制节点影响最大。
Bezier的导数及其与Hermite形式的关系
看一下Bezier曲线的导数,比如立方曲线,速度和曲线的切线向量有关,加速度和曲率有关。
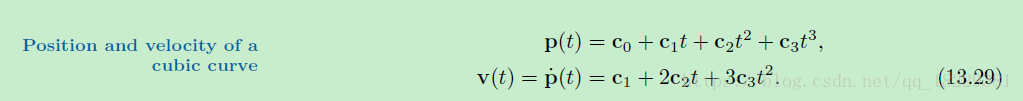
立方Bezier曲线的单项式系数
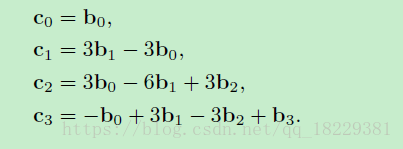
立方Bezier曲线的即时速度用控制节点表示
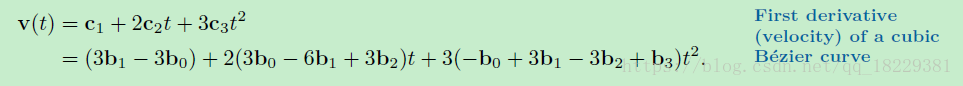
端点处速度,将t设为0或1
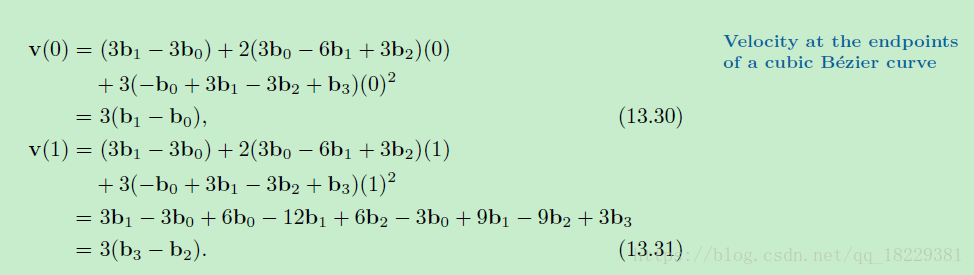
其中b1-b0是第二个控制节点到第一个控制节点的向量,b3-b2是最后一个控制点到第三个控制点的向量。所以,在曲线的开始处,t=0处的切线指向第一个控制节点,t=1处的切线指向第三个控制节点。
贝瑟儿控制多边形的第一条边决定了曲线开始处的切线,最后一条边决定了曲线终点处的切线。
另一个表示立方bezier曲线中中间控制节点角色的方法是检查Bezier形式和Hermite形式的关系。立方Hermite形式包含了初始位置p0,初始速度v0和终点位置p1、终点速度v1.现在我们知道了bezier控制节点和曲线的速度,我们就很容易从bezier形式转换到Hermite形式:

从Hermite形式到Bezier形式:

图片表示
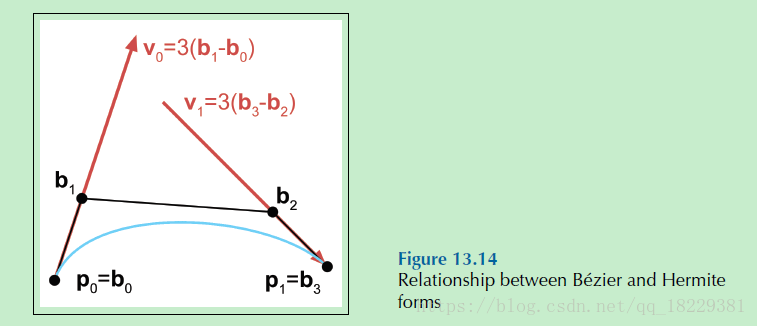
我们说过任意端点处的一阶导数完全是由最近的两个bezier控制节点决定的。我们可以把范围扩大点儿说,任意端点处的n阶导数完全是由最近的n+1个控制节点决定的。0阶导数完全由插值的控制节点决定。二阶导数(加速度)由最近的三个控制节点决定。
立方曲线加速度公式
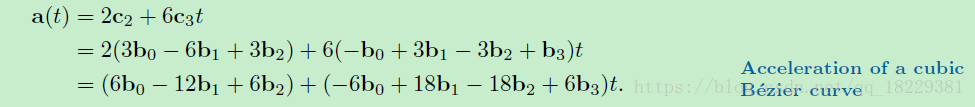
立方曲线端点处加速度
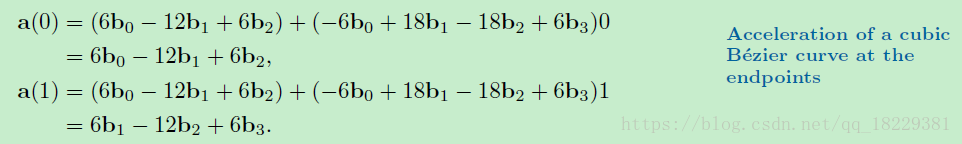
确实是由最近的3个控制点决定的。

上面的结论适用于任何度的bezier曲线,是这样的一种模式:如果移动了第i个控制节点,影响曲线开始处的第i阶或更高阶的导数,更低阶不影响;曲线结束处,如果移动了第i个控制节点,影响第n-i阶或更高阶。
怎么将曲线细分
有人会说我们不是已经有了,把原来的曲线从0到1的范围变成a到b的范围,不就是对曲线进行细分了吗?那并不是我们真正想要的,我们想要的细分曲线是完全独立的,不依赖于原有的曲线,不是从属的或者受限制的。比如说,假设我们用Bezier形式,那么我们要有定义子曲线的新的bezier控制端点。
下面的小节表示了两种细分曲线的不同方式。第一小节,描述了单项式形式的代数表示;第二小节基于几何,考虑到了Bezier曲线细分。
Hermite形式不能直接细分。如果想要对Hermite形式细分需要先转换为Bezier形式,在bezier形式进行细分。
单项式形式细分曲线
曲线其实也是无限的,只是把t限制在0到1范围内,更小的线段Q是无限曲线的更小的子集。
所以细分曲线的过程也就是参数重定向的过程。
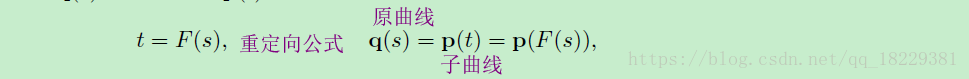
bezier形式细分曲线
bezier曲线细分可以通过一系列de Casteljau算法以几何形式完成。








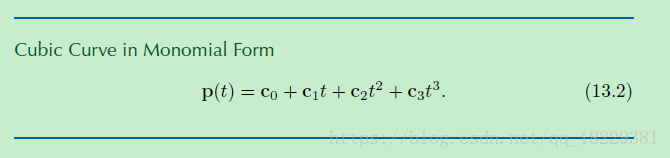















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








