设S是平面上n个点的集合,在S中找到两点p、q,使得他们的欧几里得距离d(p,q)是所有点对中最小的。
朴素的算法是计算所有点对的距离,在求出最小的,需要Ω(n2)。
采用分治法可以在Θ(nlogn)完成任务。
基本思路:
我们用分治范式来解释这一过程:
(a)划分阶段:
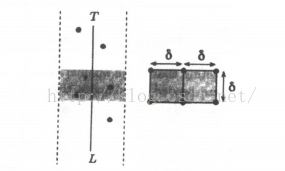
用一条垂直线L把S划分成两个尽可能大小接近的子集Sl、Sr,Sl包含左边的n/2各点,Sr包含右边的(n+1)/2个点。分别计算出Sl、Sr中的最近点对距离δl、δr。再计算Sl的点与Sr的点之间的最小距离δ’。
(b)治理阶段:
这一阶段需要计算出δ’,如果朴素的计算所有Sl中的点到Sr中所有点的距离,需要Ω(n2),并不会提高效率。幸好我们并不需要比较所有的点。
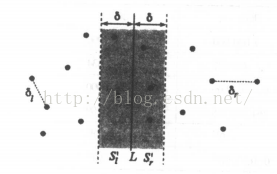
设δ=min{δl,δr},可以理解,我们要找的点不会再L两边δ距离以外的范围,只会在下图中的灰色部分,我们把这一部分称为T。
我们有下面这么一个结论:
T中的每个点最多需要和T中的7个点进行比较。(*)
下面解释一下这个结论的由来:
我们划分出δ*2δ的矩形,如果该矩形内任意两点之间的距离不超过δ,这个矩形最多能容纳8个点,其中至多4个点属于Sl,至多4个点属于Sr。但有两个点分别在矩形上下边的中点时,可以取得最大点数。因此最多只需要比较7次。
现在考虑算法中怎么得知我们需要比较哪7个点呢?
实际操作就是不要考虑,我们尽可以多比较几次,常数的增长并不会带来太大的影响。所以我们可以将T中的点按y轴坐标的增序排列,遍历所有点,但每次只计算某一点和它上面7个点的距离。这里我们进行了一些重复的操作,但保证了最后答案的可靠性,而且带来的只是常数的增长,所以还是可以接受的。
(c)组合阶段:
很明显,最近点对距离:δ=min{δl,δr,δ’}。
算法分析:
治理阶段需要排序,但我们可以先对点按x、y轴坐标进行一次排序并存储,在治理阶段只做提取的操作Θ(n),排序结果依然存在,所以我们的递推式是:
经过计算:
算法的复杂度为Θ(nlogn)。
伪代码:
*实际上只需要4个点,详见周玉林、熊鹏荣、朱洪,《求平面点集最近点对的一个改进算法》。










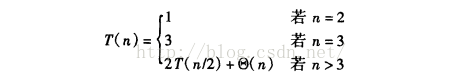
















 1224
1224











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










