【码道初阶】【LeetCode 102】二叉树层序遍历：如何利用队列实现“一层一层切蛋糕”？-CSDN博客

【LeetCode 102】二叉树层序遍历：如何利用队列实现“一层一层切蛋糕”？

在这里插入图片描述

在二叉树的遍历中，前序、中序、后序遍历通常使用递归（DFS，深度优先搜索）来实现，它们是一头扎到底再回头。

但在很多面试题中，我们需要按照“从上到下、从左到右”的顺序输出节点，这就好比切蛋糕一样，一层一层地处理。这种遍历方式被称为层序遍历（Level Order Traversal）。

解决这个问题的神器不是递归，而是队列（Queue）。今天我们就结合一段标准的 Java 代码，深入剖析**广度优先搜索（BFS）**在二叉树中的应用。

1. 核心思想：广度优先搜索 (BFS)

层序遍历的本质就是 BFS。我们需要一个“候车室”（队列）来暂存当前层的节点。

先把第一层的节点（根节点）放入候车室。
处理候车室里的节点时，顺便把它的孩子（下一层）按顺序放入候车室排队。
**先进先出（FIFO）**的特性保证了我们总是先处理完当前层，才会轮到下一层。

2. 代码深度拆解

代码采用了最经典的 BFS 迭代写法，我们可以将其分为三个阶段：

代码总览：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> list = new ArrayList<>();
            while(size != 0)
            {
                TreeNode cur = queue.poll();
                list.add(cur.val);
                if(cur.left != null) queue.offer(cur.left);
                if(cur.right != null)queue.offer(cur.right); 
                size --;           
            }
            res.add(list);
        }
        return res;
    }
}

第一阶段：初始化与判空

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> res = new ArrayList<>();
    // 1. 边界处理：如果是空树，直接返回空列表
    if(root == null) return res;
    
    // 2. 准备“候车室”：使用 LinkedList 实现 Queue 接口
    Queue<TreeNode> queue = new LinkedList<>();
    
    // 3. 将根节点入队，作为第一层
    queue.offer(root);

这里有一个细节：使用 LinkedList 来实例化 Queue 是 Java 中的标准做法，因为 LinkedList 实现了双端队列接口，入队（offer）和出队（poll）操作非常高效。

第二阶段：外层循环（遍历所有层）

    // 只要队列不空，说明还有层级没处理完
    while(!queue.isEmpty()){
        // 【关键点】记录当前队列的大小
        int size = queue.size();
        List<Integer> list = new ArrayList<>();

这是全段代码最精华的地方！
为什么要专门用一个变量 size 记录 queue.size()？

在进入内层循环前，队列里存放的仅仅是当前这一层的所有节点。
我们需要知道当前层有几个节点，这样在接下来的处理中，我们才能准确地只弹出这几个节点，而不小心处理到了新加入的下一层节点。

第三阶段：内层循环（批处理当前层）

        // 处理当前层的每一个节点
        while(size != 0)
        {
            // 1. 出队：拿出当前层的节点
            TreeNode cur = queue.poll();
            // 2. 记录值
            list.add(cur.val);
            
            // 3. 入队：如果有孩子，把它们加入队列尾部（成为下一层）
            if(cur.left != null) queue.offer(cur.left);
            if(cur.right != null) queue.offer(cur.right); 
            
            // 当前层待处理节点数 -1
            size --;           
        }
        // 当前层处理完毕，将结果加入总列表
        res.add(list);
    }
    return res;
}

在这个循环中，队列发生了一个微妙的变化：旧的一层正在离开，新的一层正在进入。
因为我们严格控制了循环次数为 size（旧层的节点数），所以即使新节点加入到了队列尾部，也不会在这一轮循环中被处理。这就完美实现了“分层”。

3. 图解执行流程

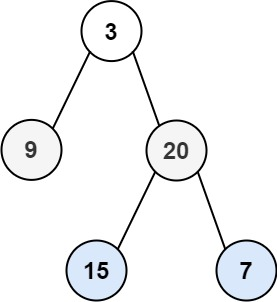
假设输入：[3, 9, 20, null, null, 15, 7]

初始状态：
- Queue: [3]
- res: []
第一轮外循环：
- size = 1。
- 内循环：弹出 3，加入 9, 20。Queue: [9, 20]。
- 内循环结束，list 为 [3]。
- res: [[3]]。
第二轮外循环：
- size = 2（此时队列里有 9 和 20）。
- 内循环第1次：弹出 9，无孩子。Queue: [20]。
- 内循环第2次：弹出 20，加入 15, 7。Queue: [15, 7]。
- 内循环结束，list 为 [9, 20]。
- res: [[3], [9, 20]]。
第三轮外循环：
- size = 2（此时队列里有 15 和 7）。
- 内循环：依次弹出 15 和 7，无新孩子加入。Queue: []。
- res: [[3], [9, 20], [15, 7]]。
结束：队列为空，退出。

4. 复杂度分析

时间复杂度： $O (N)$ 。
每个节点进队一次，出队一次，我们遍历了整棵树的 $N$ 个节点。
空间复杂度： $O (N)$ 。
- 队列中最多同时存储一层的节点。在最坏情况（完全二叉树的底层），大约包含 $N /2$ 个节点。
- 返回值列表也需要存储 $N$ 个节点的值。

5. 总结

这段代码是 BFS 解决二叉树层序遍历的标准模板。

解题的核心在于理解 Queue（队列） 的 FIFO 特性，以及利用 size 变量 对队列中的元素进行“分批处理”。掌握了这个模板，你不仅能解决这道题，还能轻松解决诸如“二叉树的锯齿形层序遍历”、“二叉树的最大深度”、“二叉树的右视图”等一系列变种题目。