算法之路--高斯分布（一）

最新推荐文章于 2024-01-28 10:09:16 发布

置顶谁能告诉我怎么取网名

最新推荐文章于 2024-01-28 10:09:16 发布

阅读量7.2k

点赞数

分类专栏：深度学习人工智能大数据算法文章标签：正态分布算法高斯分布

本文链接：https://blog.csdn.net/qq_20073741/article/details/91362105

版权

深度学习同时被 3 个专栏收录

12 篇文章 0 订阅

订阅专栏

人工智能

12 篇文章 2 订阅

订阅专栏

大数据

10 篇文章 0 订阅

订阅专栏

正态分布（英语：normal distribution）又名高斯分布（英语：Gaussian distribution），是一个非常常见的连续概率分布。正态分布在统计学上十分重要，经常用在自然和社会科学来代表一个不明的随机变量。可以判断各种情况出现的概率，进而指导下一步的操作

随机变量是取值有多种可能并且取每个值都有一个概率的变量。它分为离散型和连续型两种，离散型随机变量的取值为有限个或者无限可列个（整数集是典型的无限可列），连续型随机变量的取值为无限不可列个（实数集是典型的无限不可列）。

（一）参数含义：

æ£æåå¸å¬å¼

（1）正态分布有两个参数，即期望（均数）μ和标准差σ，σ2为方差。

（2）正态分布具有两个参数μ和σ^2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ^2是此随机变量的方差，所以正态分布记作N（μ,σ2）。

（3）μ是正态分布的位置参数，描述正态分布的集中趋势位置。概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小。正态分布以x = μ 为对称轴，左右完全对称。正态分布的均数、中位数、众数相同，均等于μ .

（4） σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。σ也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。正态曲线下面积的分布规律：如果用其标准差作为衡量单位，则以均数为中心，正负1个标准差内，即（μ-σ，μ+σ）区间内，正态分布曲线下的面积为总面积的68.27%；正负2个标准差内，即（μ-2σ，μ+2σ）区间内，面积为95.44%；正负3个标准差，即（μ-3σ，μ+3σ）区间内，面积为99.74%.这是由正态分布的性质所决定的。

（二）正态分布中一些值得注意的量：

密度函数关于平均值对称
平均值与它的众数（statistical mode）以及中位数（median）同一数值。
正态分布图像关于x=μ对称，其中μ为正态分布的期望值；
相互独立的正态分布满足加和性
正态分布的标准差越小，图像在x=μ处曲率半径越小，图像越高耸，也就是意味着取值在x=μ附近的几率越大。反之亦然；
函数曲线下68.268949%的面积在平均数左右的一个标准差范围内

横轴区间（μ-σ,μ+σ）内的面积为68.268949%。P{|X-μ|<σ}=2Φ（1）-1=0.6826。

95.449974%的面积在平均数左右两个标准差 $2 \sigma$ 的范围内。

横轴区间（μ-1.96σ,μ+1.96σ）内的面积为95.449974%。P{|X-μ|<2σ}=2Φ（2）-1=0.9544

99.730020%的面积在平均数左右三个标准差 $3 \sigma$ 的范围内。

横轴区间（μ-2.58σ,μ+2.58σ）内的面积为99.730020%。P{|X-μ|<3σ}=2Φ（3）-1=0.9974

99.993666%的面积在平均数左右四个标准差 $4 \sigma$ 的范围内。
正态分布在实际管理应用中有3σ和6σ法则；
函数曲线的拐点（inflection point）为离平均数一个标准差距离的位置。
图像的拐点在x=μ+σ和x=μ-σ处；
正态分布为中心极限定理的大样本统计分布；

若随机变量 $X$ 服从一个位置参数为 $\mu$ 、尺度参数为 $\sigma$ 的正态分布，记为：

X∼N(μ,σ2),

则其概率密度函数为

$f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{- {{(x-\mu )^2 \over 2\sigma^2}}}$

正态分布（概率密度函数）的数学期望值或期望值 $\mu$ 等于位置参数，决定了分布的位置；其方差 $\sigma^2$ 的开平方或标准差 $\sigma$ 等于尺度参数，决定了分布的幅度。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线（类似于寺庙里的大钟，因此得名）。我们通常所说的标准正态分布是位置参数 $\mu =0$ ，尺度参数 $\sigma^2 = 1$ 的正态分布（见下图中红色曲线）。

（三）概率密度函数（PDF）：

概率密度函数的含义：概率密度函数f(x)它反应了概率在x点附近的密集程度。

解释：就像质量密度不是质量一样，概率密度也不是概率。但是，质量密度表达了某一点附近所含有质量的多寡。同样，某一点处的概率密度，也表达了随机变量落入那一点附近的概率的大小程度。假设，在X=a处概率密度为0.1，在X=b处的概率密度为0.2，那么随机变量落入b附近的概率比之随机变量落入a附近的概率要大。

正态分布的概率密度函数均值为 $\mu$ 方差为 $\sigma^2$ (或标准差 $\sigma$ )是高斯函数的一个实例：

$f(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \, \exp \left( -\frac{(x- \mu)^2}{2\sigma^2} \right)$ 。

(请看指数函数以及 $\pi$ .)

如果一个随机变量 $X$ 服从这个分布，我们写作 $X$ X∼N(μ,σ2). 如果 $\mu =0$ 并且 $\sigma =1$ ，这个分布被称为标准正态分布，这个分布能够简化为

$f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right)$ $f(x) = \frac{1}{\sqrt{2\pi}} \, \exp\left(-\frac{x^2}{2} \right)$

（四）累计分布函数(CDF)

累积分布函数的作用：

1.为什么需要分布函数？

　　对于离散型随机变量，可以直接用分布律来描述其统计规律性，而对于非离散型的随机变量，如连续型随机变量，因为我们无法一一列举出随机变量的所有可能取值，所以它的概率分布不能像随机变量那样进行描述，于是引入PDF，用积分来求随机变量落入某个区间的概率。分布律不能描述连续型随机变量，密度函数不能描述离散随机变量，因此需要找到一个统一方式描述随机变量统计规律，这就有了分布函数。另外，在现实生活中，有时候人们感兴趣的是随机变量落入某个范围内的概率是多少，如掷骰子的数小于3点的获胜，那么考虑随机变量落入某个区间的概率就变得有现实意义了，因此引入分布函数很有必要。

2. 分布函数的意义

　　分布函数F(x)在点x处的函数值表示X落在区间(−∞,x]内的概率，所以分布函数就是定义域为R的一个普通函数，因此我们可以把概率问题转化为函数问题，从而可以利用普通的函数知识来研究概率问题，增大了概率的研究范围。

累积分布函数是指随机变量X小于或等于x的概率，用密度函数表示为

$F(x;\mu,\sigma)=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^x \exp \left( -\frac{(x - \mu)^2}{2\sigma^2}\ \right)\, dx.$

正态分布的累积分布函数能够由一个叫做误差函数的特殊函数表示：

$\Phi(z)=\frac12 \left[1 + \mathrm{erf}\,(\frac{z-\mu}{\sigma\sqrt2})\right] .$

标准正态分布的累积分布函数习惯上记为Φ，它仅仅是指μ = 0，σ = 1时的值，

$\Phi(x)=F(x;0,1)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x\exp\left(-\frac{x^2}{2}\right)\, dx.$

将一般正态分布用误差函数表示的公式简化，可得：

$\Phi(z)=\frac{1}{2} \left[ 1 + \operatorname{erf} \left( \frac{z}{\sqrt{2}} \right) \right].$

它的反函数被称为反误差函数，为：

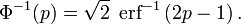
$\Phi^{-1}(p)=\sqrt2\;\operatorname{erf}^{-1} \left(2p - 1 \right).$

该分位数函数有时也被称为probit函数。probit函数已被证明没有初等原函数。

正态分布的分布函数Φ(x)没有解析表达式，它的值可以通过数值积分、泰勒级数或者渐进序列近似得到。

（五）概念及特征：

一、正态分布的概念

由一般分布的频数表资料所绘制的直方图，图⑴可以看出，高峰位于中部，左右两侧大致对称。我们

正态分布研究图1

设想，如果观察例数逐渐增多，组段不断分细，直方图顶端的连线就会逐渐形成一条高峰位于中央（均数所在处），两侧逐渐降低且左右对称，不与横轴相交的光滑曲线图⑶。这条曲线称为频数曲线或频率曲线，近似于数学上的正态分布（normal distribution）。由于频率的总和为100%或1，故该曲线下横轴上的面积为100%或1。

为了应用方便，常对正态分布变量X作变量变换。

该变换使原来的正态分布转化为标准正态分布（standard normal distribution），亦称u分布。u被称为标准正态变量或标准正态离差（standard normal deviate）。

正态分布研究图2

正态分布研究图3

实际工作中，常需要了解正态曲线下横轴上某一区间的面积占总面积的百分数，以便估计该区间的例数占总例数的百分数（频数分布）或观察值落在该区间的概率。正态曲线下一定区间的面积可以通过附表1求得。对于正态或近似正态分布的资料，已知均数和标准差，就可对其频数分布作出概约估计。

查附表1应注意：①表中曲线下面积为-∞到u的左侧累计面积；②当已知μ、σ和X时先按式u=（X-μ）/σ求得u值，再查表，当μ、σ未知且样本含量n足够大时，可用样本均数X1和标准差S分别代替μ和σ，按u=（X-X1）/S式求得u值，再查表；③曲线下对称于0的区间面积相等，如区间（-∞，-1.96）与区间（1.96，∞）的面积相等，④曲线下横轴上的总面积为100%或1。

图2 正态曲线与标准正态曲线的面积分布

正态分布的应用某些医学现象，如同质群体的身高、红细胞数、血红蛋白量、胆固醇等，以及实验中的随机误差，呈现为正态或近似正态分布；有些资料虽为偏态分布，但经数据变换后可成为正态或近似正态分布，故可按正态分布规律处理。

正态分布面积图1

正态分布面积图2

一般正态分布与标准正态分布的区别与联系

正态分布也叫常态分布，是连续随机变量概率分布的一种，自然界、人类社会、心理和教育中大量现象均按正态形式分布，例如能力的高低，学生成绩的好坏等都属于正态分布。它随随机变量的平均数、标准差的大小与单位不同而有不同的分布形态。标准正态分布是正态分布的一种，其平均数和标准差都是固定的，平均数为0，标准差为1。

（六）例子

例1.10 某地1993年抽样调查了100名18岁男大学生身高（cm），其均数=172.70cm，标准差s=4.01cm，①估计该地18岁男大学生身高在168cm以下者占该地18岁男大学生总数的百分数；②分别求X+-1s、X+-1.96s、X+-2.58s范围内18岁男大学生占该地18岁男大学生总数的实际百分数，并与理论百分数比较。

本例，μ、σ未知但样本含量n较大，按式（3.1）用样本均数X和标准差S分别代替μ和σ，求得u值，u=（168-172.70）/4.01=-1.17。查附表标准正态曲线下的面积，在附录表的左侧找到-1.1，表的上方找到0.07，两者相交处为0.8790。1-0.8790=0.1210=12.10%。该地18岁男大学生身高在168cm以下者，约占总数12.10%。其它计算结果见表3。

X=172.70,s=4.04。

X+-s=172.70-4.04~172.70+4.04

X+-1.96s=172.70-1.96*4.04~172.70+1.96*4.04

表3 100名18岁男大学生身高的实际分布与理论分布

分布 x+-s	身高范围（cm）	实际分布人数	实际分布百分数（%）	理论分布（%）
X+-1s	168.69～176.71	67	67.00	68.27
X +-1.96s	164.84～180.56	95	95.00	95.00
X+-2.58s	162.35～183.05	99	99.00	99.00

例2：

某饮料公司装瓶流程严谨，每罐饮料装填量符合平均600毫升，标准差3毫升的正态分配法则。随机选取一罐，求（1）容量超过605毫升的概率；（2）容量小于590毫升的概率。

容量超过605毫升的概率 = p ( X > 605)= p ( ((X-μ) /σ) > ( (605 – 600) / 3) )= p ( Z > 5/3) = p( Z > 1.67) = 1 - 0.9525 = 0.0475

容量小于590毫升的概率 = p (X < 590) = p ( ((X-μ) /σ) < ( (590 – 600) / 3) )= p ( Z < -10/3) = p( Z < -3.33) = 0.0004

例3：计算学生智商高低的概率

假设某校入学新生的智力测验平均分数与标准差分别为100与12。那么随机抽取50个学生，他们智力测验平均分数大于105的概率？小于90的概率？

本例没有正态分配的假设，还好中心极限定理提供一个可行解，那就是当随机样本长度超过30，样本平均数 $\bar{x}$ 近似于一个正态变量，

因此标准正态变量 $Z={\frac {{\bar {X}}-\mu }{\sigma /{\sqrt {n}}}}$ 。

平均分数大于105的概率 P(Z>{105-100})=P(Z>5/1.7)=P(Z>2.94)=0.0016} $P(Z>{\frac {105-100}{12/{\sqrt {50}}}})=P(Z>5/1.7)=P(Z>2.94)=0.0016$

平均分数小于90的概率 {P(Z< {90-100}})}=P(Z<-5.88)=0.0000} $P(Z<{\frac {90-100}{12/{\sqrt {50}}}})=P(Z<-5.88)=0.0000$

附录一：

查表定位例如要查假设X=1.15，

1)左边一列找到1.1的标准正态分布表

2)上面一行找到0.05

3)1.1和 0.05所对应的值为 0.8749。

谁能告诉我怎么取网名

关注

0
点赞
踩
8

收藏

觉得还不错? 一键收藏
0
评论
算法之路--高斯分布（一）

正态分布（英语：normal distribution）又名高斯分布（英语：Gaussian distribution），是一个非常常见的连续概率分布。正态分布在统计学上十分重要，经常用在自然和社会科学来代表一个不明的随机变量。可以判断各种情况出现的概率，进而指导下一步的操作随机变量是取值有多种可能并且取每个值都有一个概率的变量。它分为离散型和连续型两种，离散型随机变量的取值为有限个或者...
复制链接

扫一扫