leetcode-312：戳气球

最新推荐文章于 2023-05-13 10:44:49 发布

原创最新推荐文章于 2023-05-13 10:44:49 发布 · 192 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #深度优先

leetcode 专栏收录该内容

612 篇文章

订阅专栏

该博客详细介绍了LeetCode 312题目的解题方法，包括记忆化搜索（DFS）和动态规划两种策略。作者通过示例解释了题目的要求，并提供了两种方法的代码实现，强调了动态规划中遍历顺序的重要性。

leetcode-312：戳气球

题目
解题
- 方法一：记忆化+dfs
- 方法二：动态规划

题目

题目连接

有 n 个气球，编号为0 到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums 中。

现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。

求所能获得硬币的最大数量。

示例 1：

输入：nums = [3,1,5,8]
输出：167

解释：

nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins =  3*1*5    +   3*5*8   +  1*3*8  + 1*8*1 = 167

示例 2：

输入：nums = [1,5]
输出：10

解题

方法一：记忆化+dfs

参考链接

class Solution {
public:
    vector<vector<int>> dp;
    vector<int> nums;
    int dfs(int left,int right){
        if(left>=right-1) return 0;
        if(dp[left][right]!=-1){
            return dp[left][right];
        }
        for(int i=left+1;i<right;i++){
            int sum=nums[left]*nums[i]*nums[right];
            sum+=dfs(left,i)+dfs(i,right);
            dp[left][right]=max(dp[left][right],sum);
        }
        return dp[left][right];
    }
    int maxCoins(vector<int>& nums) {
        int n=nums.size();
        nums.insert(nums.begin(),1);
        nums.push_back(1);
        this->nums=nums;
        dp=vector<vector<int>>(n+2,vector<int>(n+2,-1));
        return dfs(0,n+1);
    }
};

方法二：动态规划

注意遍历顺序

class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n=nums.size();
        nums.insert(nums.begin(),1);
        nums.push_back(1);
        vector<vector<int>> dp(n+2,vector<int>(n+2));
        for(int i=n-1;i>=0;i--){
            for(int j=i+2;j<=n+1;j++){
                for(int k=i+1;k<j;k++){
                    int sum=nums[i]*nums[k]*nums[j];
                    sum+=dp[i][k]+dp[k][j];
                    dp[i][j]=max(dp[i][j],sum);
                }
            }
        }
        return dp[0][n+1];
    }
};

或者换种遍历顺序

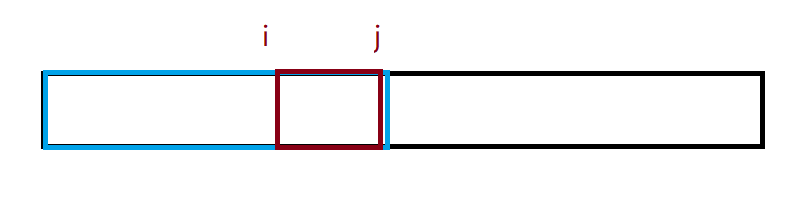
比如要计算蓝色的这部分dp值，那么首先要计算dp[i][j]，i要从j-2开始，向左边遍历。因为计算蓝色部分的dp值会用到这部分
在这里插入图片描述

class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n=nums.size();
        nums.insert(nums.begin(),1);
        nums.push_back(1);
        vector<vector<int>> dp(n+2,vector<int>(n+2));
        for(int j=2;j<=n+1;j++){
            for(int i=j-2;i>=0;i--){
                for(int k=i+1;k<j;k++){
                    int sum=nums[i]*nums[k]*nums[j];
                    sum+=dp[i][k]+dp[k][j];
                    dp[i][j]=max(dp[i][j],sum);
                }
            }
        }
        return dp[0][n+1];
    }
};