目录
四、因子分解机(Factorization Machine)
2.2.2 矩阵分解方法与因子分解机方法
一、引言
在上一节中,我们详细探讨了基于记忆的协同过滤算法,了解了其基本原理、实现方法以及优缺点。基于记忆的方法虽然直观易懂,但随着用户和物品数量的增长,面临着计算复杂度高、可扩展性差、数据稀疏性等挑战。这些问题催生了基于模型的协同过滤方法,其中最经典、最成功的就是矩阵分解(Matrix Factorization, MF) 方法。
矩阵分解方法通过将用户-物品交互矩阵分解为两个低维矩阵的乘积,将用户和物品映射到同一低维潜在空间中。这种方法不仅大大减少了计算复杂度,还能有效处理数据稀疏性问题,并发现用户和物品之间的潜在关联。
在本节中,我们将深入探讨矩阵分解方法,从基础的奇异值分解(SVD)到更先进的因子分解机(Factorization Machine, FM),并介绍它们在推荐系统中的应用。我们还将通过完整的Python实现来帮助读者理解这些算法的原理和实现细节。
二、矩阵分解的基本原理
1. 从协同过滤到矩阵分解
基于记忆的协同过滤直接使用用户-物品交互矩阵进行预测,而矩阵分解则通过学习用户和物品的潜在特征(latent features) 来间接进行预测。这些潜在特征通常被称为潜在因子(latent factors),它们代表了用户偏好和物品特性的抽象表示。
核心思想:
将用户-物品交互矩阵R(m×n,m个用户,n个物品)分解为两个低维矩阵的乘积:
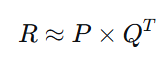
其中:
-
P是m×k的用户潜在特征矩阵
-
Q是n×k的物品潜在特征矩阵
-
k是潜在特征的数量(通常k ≪ m, n)
这样,用户u对物品i的预测评分可以表示为:
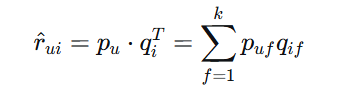
其中$p_u$是用户u的潜在特征向量,$q_i$是物品i的潜在特征向量。
2. 矩阵分解的数学优化
矩阵分解的目标是找到用户特征矩阵P和物品特征矩阵Q,使得它们的乘积尽可能接近原始评分矩阵R。这可以通过最小化以下损失函数来实现:
基础损失函数:
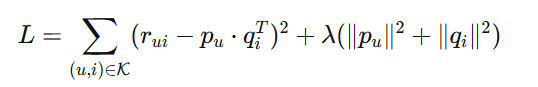
其中:
-
$\mathcal{K}$是已知评分的集合
-
$\lambda$是正则化系数,防止过拟合
-
第二项是L2正则化项
优化方法:
常用的优化方法包括:
-
随机梯度下降(SGD):每次迭代更新一个评分对应的用户和物品向量
-
交替最小二乘法(ALS):固定一个矩阵,优化另一个矩阵,交替进行
-
加权交替最小二乘法(WALS):ALS的加权版本,可以处理隐式反馈
3. 矩阵分解的优势
相比于基于记忆的协同过滤,矩阵分解具有以下优势:
-
可扩展性好:计算复杂度与用户和物品数量呈线性关系
-
处理稀疏数据:通过低维表示学习,能够从稀疏数据中提取有用信息
-
灵活性高:可以方便地加入各种约束和扩展
-
发现潜在关系:能够发现用户和物品之间非显而易见的关联
-
预测精度高:在实践中通常比基于记忆的方法表现更好
三、奇异值分解(SVD)及其变体
1. 传统SVD
奇异值分解(Singular Value Decomposition)是矩阵分解的经典方法。对于一个m×n的实数矩阵R,SVD将其分解为:
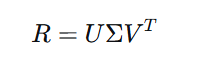
其中:
-
U是m×m的正交矩阵(左奇异向量)
-
Σ是m×n的对角矩阵(奇异值)
-
V是n×n的正交矩阵(右奇异向量)
在推荐系统中,我们通常使用截断SVD,只保留前k个最大的奇异值及其对应的奇异向量:
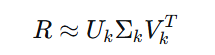
其中$U_k$是m×k,$\Sigma_k$是k×k,$V_k$是n×k。
局限性:
传统SVD要求矩阵是稠密的,而推荐系统中的用户-物品矩阵通常是稀疏的,因此需要特殊处理。
2. 基于SVD的协同过滤
为了解决稀疏性问题,Simon Funk在2006年Netflix Prize竞赛中提出了基于SVD的协同过滤方法,通常称为FunkSVD。这种方法直接优化用户和物品的潜在特征矩阵,只考虑已知评分。
FunkSVD算法:
-
随机初始化用户矩阵P和物品矩阵Q
-
对于每个已知评分$r_{ui}$:
-
计算预测误差:$e_{ui} = r_{ui} - p_u \cdot q_i^T$
-
更新用户向量:$p_u \leftarrow p_u + \eta (e_{ui} q_i - \lambda p_u)$
-
更新物品向量:$q_i \leftarrow q_i + \eta (e_{ui} p_u - \lambda q_i)$
-
-
重复步骤2直到收敛或达到最大迭代次数
其中$\eta$是学习率,$\lambda$是正则化系数。
3. 偏置SVD(Biased SVD)
在真实数据中,不同用户的评分习惯不同(有些用户倾向于打高分,有些则相反),不同物品的受欢迎程度也不同。偏置SVD通过引入用户偏置和物品偏置来建模这些系统性的偏差:
偏置SVD模型:
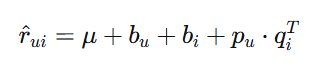
其中:
-
$\mu$是全局平均评分
-
$b_u$是用户偏置(用户u的评分习惯)
-
$b_i$是物品偏置(物品i的受欢迎程度)
损失函数:
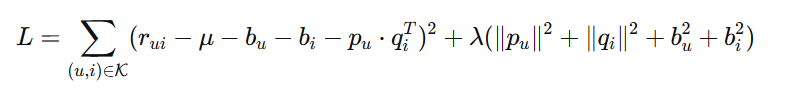
4. SVD++
SVD++是对偏置SVD的进一步扩展,它考虑了用户的隐式反馈。除了显式评分,用户的行为(如浏览、点击、收藏)也包含了用户的偏好信息。
SVD++模型:
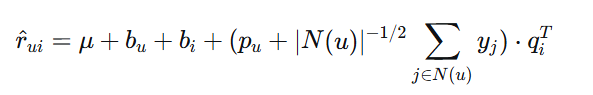
其中:
-
$N(u)$是用户u有隐式反馈的物品集合
-
$y_j$是物品j的隐式反馈特征向量
SVD++能够同时利用显式评分和隐式反馈,通常能获得更好的预测性能。
四、因子分解机(Factorization Machine)
1. 因子分解机的基本原理
因子分解机(Factorization Machine, FM)是Steffen Rendle于2010年提出的一种通用预测模型,特别适合处理高维稀疏数据。FM不仅可以用于推荐系统,还可以用于各种分类和回归任务。
FM模型方程:
对于特征向量$x \in \mathbb{R}^n$,FM的预测值为:
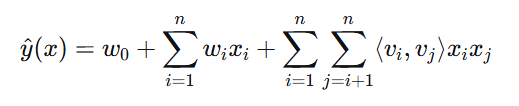
其中:
-
$w_0$是全局偏置
-
$w_i$是第i个特征的权重
-
$v_i \in \mathbb{R}^k$是第i个特征的k维潜在向量
-
$\langle v_i, v_j \rangle = \sum_{f=1}^k v_{i,f} v_{j,f}$是向量点积
FM的特点:
-
处理高维稀疏数据:通过因子化参数,即使特征组合没有出现在训练数据中,也能进行预测
-
线性时间复杂度:计算复杂度为O(kn),其中k是潜在因子维度,n是特征数量
-
通用性:可用于回归、二分类、排序等任务
2. FM与矩阵分解的关系
当我们将FM应用于推荐系统时,可以将其看作是矩阵分解的泛化。考虑一个简单的推荐场景,特征向量x包含用户one-hot编码和物品one-hot编码,那么:
-
$w_0$对应全局平均评分
-
用户和物品的one-hot特征对应的$w_i$分别对应用户偏置和物品偏置
-
用户和物品特征的交互项$\langle v_u, v_i \rangle$对应矩阵分解中的$p_u \cdot q_i^T$
因此,FM可以看作是包含了偏置项的矩阵分解的扩展。
3. FM的优化计算
FM模型中的二阶交互项看似需要O(n²)的计算复杂度,但实际上可以通过数学变换将其降低到O(kn):
计算优化:
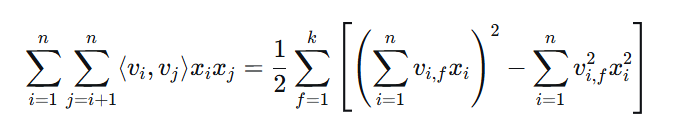
这样,我们可以在线性时间内计算FM的预测值,这是FM能够高效处理高维数据的关键。
4. FM的扩展
场感知因子分解机(Field-aware FM, FFM):
FFM是FM的扩展,它考虑了特征属于不同的"场"(field)。在FFM中,每个特征针对不同的场有不同的潜在向量,这增加了模型的表达能力,但也增加了参数数量和计算复杂度。
高阶FM:
标准FM只考虑了二阶特征交互,可以扩展到更高阶:
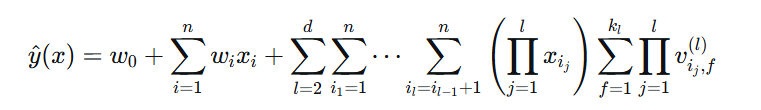
其中d是交互的最高阶数。但高阶FM的计算复杂度会指数增长,实际中较少使用。
五、完整Python实现
下面我们通过一个完整的Python案例来演示矩阵分解和因子分解机方法的实现、应用和评估:
import numpy as np
import matplotlib.pyplot as plt
from collections import defaultdict
import warnings
warnings.filterwarnings('ignore')
class MatrixFactorization:
"""矩阵分解推荐系统"""
def __init__(self, n_factors=10, learning_rate=0.01, reg_param=0.02,
n_epochs=100, method='sgd', verbose=True):
"""
初始化矩阵分解模型
参数:
n_factors: 潜在因子数量
learning_rate: 学习率
reg_param: 正则化参数
n_epochs: 训练轮数
method: 优化方法 ('sgd' 或 'als')
verbose: 是否输出训练过程
"""
self.n_factors = n_factors
self.learning_rate = learning_rate
self.reg_param = reg_param
self.n_epochs = n_epochs
self.method = method
self.verbose = verbose
self.user_factors = None
self.item_factors = None
self.user_biases = None
self.item_biases = None
self.global_bias = None
def fit(self, ratings):
"""
训练矩阵分解模型
参数:
ratings: 用户-物品评分矩阵,shape=(n_users, n_items)
"""
self.n_users, self.n_items = ratings.shape
self.ratings = ratings
# 获取已知评分的索引
self.known_ratings = np.argwhere(ratings != 0)
# 计算全局平均评分
self.global_bias = np.mean(ratings[ratings != 0])
# 初始化参数
self._init_parameters()
# 训练模型
if self.method == 'sgd':
self._train_sgd()
elif self.method == 'als':
self._train_als()
else:
raise ValueError(f"未知的优化方法: {self.method}")
return self
def _init_parameters(self):
"""初始化模型参数"""
# 随机初始化用户和物品的潜在因子
self.user_factors = np.random.normal(0, 0.1, (self.n_users, self.n_factors))
self.item_factors = np.random.normal(0, 0.1, (self.n_items, self.n_factors))
# 初始化偏置项
self.user_biases = np.zeros(self.n_users)
self.item_biases = np.zeros(self.n_items)
def _train_sgd(self):
"""使用随机梯度下降训练模型"""
if self.verbose:
print("开始SGD训练...")
for epoch in range(self.n_epochs):
epoch_loss = 0
np.random.shuffle(self.known_ratings)
for u, i in self.known_ratings:
actual_rating = self.ratings[u, i]
predicted_rating = self.predict_single(u, i)
# 计算误差
error = actual_rating - predicted_rating
epoch_loss += error ** 2
# 更新参数
user_factor_grad = error * self.item_factors[i] - self.reg_param * self.user_factors[u]
item_factor_grad = error * self.user_factors[u] - self.reg_param * self.item_factors[i]
user_bias_grad = error - self.reg_param * self.user_biases[u]
item_bias_grad = error - self.reg_param * self.item_biases[i]
self.user_factors[u] += self.learning_rate * user_factor_grad
self.item_factors[i] += self.learning_rate * item_factor_grad
self.user_biases[u] += self.learning_rate * user_bias_grad
self.item_biases[i] += self.learning_rate * item_bias_grad
# 计算本轮平均损失
epoch_loss /= len(self.known_ratings)
if self.verbose and (epoch + 1) % 10 == 0:
print(f"Epoch {epoch+1}/{self.n_epochs}, Loss: {epoch_loss:.4f}")
def _train_als(self):
"""使用交替最小二乘法训练模型"""
if self.verbose:
print("开始ALS训练...")
for epoch in range(self.n_epochs):
epoch_loss = 0
# 固定物品因子,更新用户因子
for u in range(self.n_users):
# 获取用户u评过分的物品索引
rated_items = np.where(self.ratings[u] != 0)[0]
if len(rated_items) > 0:
# 构建矩阵和向量
A = np.dot(self.item_factors[rated_items].T, self.item_factors[rated_items])
A += self.reg_param * np.eye(self.n_factors)
b = np.dot(self.item_factors[rated_items].T,
self.ratings[u, rated_items] - self.global_bias - self.item_biases[rated_items])
# 更新用户因子和偏置
self.user_factors[u] = np.linalg.solve(A, b)
self.user_biases[u] = np.mean(self.ratings[u, rated_items] -
self.global_bias - self.item_biases[rated_items] -
np.dot(self.item_factors[rated_items], self.user_factors[u]))
# 固定用户因子,更新物品因子
for i in range(self.n_items):
# 获取评价过物品i的用户索引
rated_users = np.where(self.ratings[:, i] != 0)[0]
if len(rated_users) > 0:
# 构建矩阵和向量
A = np.dot(self.user_factors[rated_users].T, self.user_factors[rated_users])
A += self.reg_param * np.eye(self.n_factors)
b = np.dot(self.user_factors[rated_users].T,
self.ratings[rated_users, i] - self.global_bias - self.user_biases[rated_users])
# 更新物品因子和偏置
self.item_factors[i] = np.linalg.solve(A, b)
self.item_biases[i] = np.mean(self.ratings[rated_users, i] -
self.global_bias - self.user_biases[rated_users] -
np.dot(self.user_factors[rated_users], self.item_factors[i]))
# 计算本轮损失
for u, i in self.known_ratings:
predicted_rating = self.predict_single(u, i)
epoch_loss += (self.ratings[u, i] - predicted_rating) ** 2
epoch_loss /= len(self.known_ratings)
if self.verbose and (epoch + 1) % 10 == 0:
print(f"Epoch {epoch+1}/{self.n_epochs}, Loss: {epoch_loss:.4f}")
def predict_single(self, u, i):
"""预测用户u对物品i的评分"""
if self.user_factors is None or self.item_factors is None:
raise ValueError("模型尚未训练")
return (self.global_bias + self.user_biases[u] + self.item_biases[i] +
np.dot(self.user_factors[u], self.item_factors[i]))
def predict_all(self):
"""预测所有用户对所有物品的评分"""
predictions = np.zeros((self.n_users, self.n_items))
for u in range(self.n_users):
for i in range(self.n_items):
predictions[u, i] = self.predict_single(u, i)
return predictions
def recommend_for_user(self, user_id, top_n=5):
"""为用户生成推荐列表"""
if user_id >= self.n_users:
raise ValueError(f"用户ID {user_id} 超出范围")
# 获取用户尚未评分的物品
unrated_items = np.where(self.ratings[user_id] == 0)[0]
# 预测用户对这些物品的评分
predictions = []
for i in unrated_items:
pred_rating = self.predict_single(user_id, i)
predictions.append((i, pred_rating))
# 按预测评分排序
predictions.sort(key=lambda x: x[1], reverse=True)
return predictions[:top_n]
def evaluate(self, test_ratings):
"""评估模型性能"""
test_indices = np.argwhere(test_ratings != 0)
predictions = []
actuals = []
for u, i in test_indices:
pred = self.predict_single(u, i)
actual = test_ratings[u, i]
predictions.append(pred)
actuals.append(actual)
# 计算评估指标
mse = np.mean((np.array(actuals) - np.array(predictions)) ** 2)
rmse = np.sqrt(mse)
mae = np.mean(np.abs(np.array(actuals) - np.array(predictions)))
return {
'mse': mse,
'rmse': rmse,
'mae': mae,
'predictions': predictions,
'actuals': actuals
}
class FactorizationMachine:
"""因子分解机"""
def __init__(self, n_factors=10, learning_rate=0.01, reg_param=0.01,
n_epochs=100, verbose=True):
"""
初始化因子分解机
参数:
n_factors: 潜在因子维度
learning_rate: 学习率
reg_param: 正则化参数
n_epochs: 训练轮数
verbose: 是否输出训练过程
"""
self.n_factors = n_factors
self.learning_rate = learning_rate
self.reg_param = reg_param
self.n_epochs = n_epochs
self.verbose = verbose
self.w0 = None # 全局偏置
self.w = None # 特征权重
self.v = None # 特征潜在向量
def _preprocess_features(self, X):
"""预处理特征"""
# 这里简化处理,假设X已经是数值特征
# 在实际应用中,可能需要处理分类特征、归一化等
return X
def fit(self, X, y):
"""
训练因子分解机
参数:
X: 特征矩阵,shape=(n_samples, n_features)
y: 目标值,shape=(n_samples,)
"""
self.n_samples, self.n_features = X.shape
self.X = self._preprocess_features(X)
self.y = y
# 初始化参数
self._init_parameters()
# 训练模型
self._train()
return self
def _init_parameters(self):
"""初始化模型参数"""
self.w0 = 0.0
self.w = np.zeros(self.n_features)
self.v = np.random.normal(0, 0.1, (self.n_features, self.n_factors))
def _train(self):
"""训练模型"""
if self.verbose:
print("开始训练因子分解机...")
for epoch in range(self.n_epochs):
epoch_loss = 0
for idx in range(self.n_samples):
x = self.X[idx]
y_true = self.y[idx]
# 预测
y_pred = self._predict_single(x)
# 计算误差
error = y_true - y_pred
epoch_loss += error ** 2
# 更新参数
self._update_parameters(x, error)
# 计算本轮平均损失
epoch_loss /= self.n_samples
if self.verbose and (epoch + 1) % 10 == 0:
print(f"Epoch {epoch+1}/{self.n_epochs}, Loss: {epoch_loss:.4f}")
def _predict_single(self, x):
"""预测单个样本"""
# 线性项
linear_term = self.w0 + np.dot(self.w, x)
# 交互项(优化计算)
interaction_term = 0
sum_vx = np.dot(self.v.T, x) # shape=(n_factors,)
for f in range(self.n_factors):
interaction_term += np.sum((sum_vx[f] ** 2) - np.sum((self.v[:, f] ** 2) * (x ** 2)))
interaction_term *= 0.5
return linear_term + interaction_term
def _update_parameters(self, x, error):
"""更新模型参数"""
# 更新全局偏置
self.w0 += self.learning_rate * error
# 更新特征权重
for j in range(self.n_features):
if x[j] != 0:
# 计算梯度
w_grad = error * x[j] - self.reg_param * self.w[j]
self.w[j] += self.learning_rate * w_grad
# 更新潜在向量
for f in range(self.n_factors):
# 计算梯度
sum_vx = np.dot(self.v[:, f], x)
v_grad = error * (x[j] * (sum_vx - self.v[j, f] * x[j])) - self.reg_param * self.v[j, f]
self.v[j, f] += self.learning_rate * v_grad
def predict(self, X):
"""预测"""
X_processed = self._preprocess_features(X)
predictions = np.zeros(X_processed.shape[0])
for i in range(X_processed.shape[0]):
predictions[i] = self._predict_single(X_processed[i])
return predictions
def evaluate(self, X_test, y_test):
"""评估模型性能"""
predictions = self.predict(X_test)
mse = np.mean((y_test - predictions) ** 2)
rmse = np.sqrt(mse)
mae = np.mean(np.abs(y_test - predictions))
return {
'mse': mse,
'rmse': rmse,
'mae': mae,
'predictions': predictions
}
def create_movie_dataset():
"""创建电影评分数据集"""
np.random.seed(42)
# 创建用户-物品评分矩阵
n_users = 50
n_items = 100
n_factors = 5 # 真实潜在因子数量
# 生成真实的用户和物品潜在因子
true_user_factors = np.random.normal(0, 1, (n_users, n_factors))
true_item_factors = np.random.normal(0, 1, (n_items, n_factors))
# 生成真实评分矩阵
true_ratings = np.dot(true_user_factors, true_item_factors.T)
# 添加偏置
user_biases = np.random.normal(0, 0.5, n_users)
item_biases = np.random.normal(0, 0.5, n_items)
global_bias = 3.5
for u in range(n_users):
for i in range(n_items):
true_ratings[u, i] += global_bias + user_biases[u] + item_biases[i]
# 归一化到1-5分
true_min, true_max = true_ratings.min(), true_ratings.max()
true_ratings = 1 + 4 * (true_ratings - true_min) / (true_max - true_min)
# 添加噪声
ratings = true_ratings + np.random.normal(0, 0.5, (n_users, n_items))
ratings = np.clip(ratings, 1, 5)
# 创建稀疏矩阵(模拟真实场景)
sparse_ratings = np.zeros((n_users, n_items))
sparsity = 0.95 # 95%的评分缺失
for u in range(n_users):
for i in range(n_items):
if np.random.random() > sparsity:
sparse_ratings[u, i] = ratings[u, i]
return sparse_ratings, true_ratings, true_user_factors, true_item_factors
def create_fm_dataset(n_samples=1000, n_features=50, sparsity=0.9):
"""创建因子分解机数据集"""
np.random.seed(42)
# 生成稀疏特征矩阵
X = np.zeros((n_samples, n_features))
for i in range(n_samples):
# 每个样本随机激活少量特征
active_features = np.random.choice(n_features, size=int(n_features * (1-sparsity)), replace=False)
X[i, active_features] = np.random.uniform(0, 1, len(active_features))
# 生成真实权重和潜在向量
true_w0 = 2.0
true_w = np.random.normal(0, 0.5, n_features)
true_v = np.random.normal(0, 0.1, (n_features, 5)) # 5个潜在因子
# 生成目标值
y = np.zeros(n_samples)
for i in range(n_samples):
# 线性项
linear = true_w0 + np.dot(true_w, X[i])
# 交互项
interaction = 0
for f in range(5):
sum_vx = np.dot(true_v[:, f], X[i])
interaction += np.sum((sum_vx ** 2) - np.sum((true_v[:, f] ** 2) * (X[i] ** 2)))
interaction *= 0.5
y[i] = linear + interaction + np.random.normal(0, 0.1)
return X, y, true_w0, true_w, true_v
def compare_matrix_factorization_methods():
"""比较不同的矩阵分解方法"""
print("="*60)
print("矩阵分解方法比较")
print("="*60)
# 创建数据集
ratings, true_ratings, true_user_factors, true_item_factors = create_movie_dataset()
n_users, n_items = ratings.shape
print(f"数据集信息:")
print(f" 用户数: {n_users}")
print(f" 物品数: {n_items}")
print(f" 评分数量: {np.count_nonzero(ratings)}")
print(f" 稀疏度: {(ratings.size - np.count_nonzero(ratings)) / ratings.size:.2%}")
# 划分训练集和测试集
train_ratings = ratings.copy()
test_ratings = np.zeros_like(ratings)
# 随机选择20%的已知评分作为测试集
known_indices = np.argwhere(ratings != 0)
np.random.seed(42)
test_indices = known_indices[np.random.choice(len(known_indices),
size=int(0.2 * len(known_indices)),
replace=False)]
for u, i in test_indices:
test_ratings[u, i] = ratings[u, i]
train_ratings[u, i] = 0
print(f"\n数据划分:")
print(f" 训练集评分数: {np.count_nonzero(train_ratings)}")
print(f" 测试集评分数: {np.count_nonzero(test_ratings)}")
# 测试不同的矩阵分解方法
methods = ['sgd', 'als']
results = {}
for method in methods:
print(f"\n{'='*40}")
print(f"训练{method.upper()}矩阵分解模型")
print('='*40)
# 创建并训练模型
mf = MatrixFactorization(n_factors=10, learning_rate=0.01,
reg_param=0.02, n_epochs=50,
method=method, verbose=True)
mf.fit(train_ratings)
# 评估模型
eval_results = mf.evaluate(test_ratings)
results[method] = eval_results
print(f"\n{method.upper()} 评估结果:")
print(f" RMSE: {eval_results['rmse']:.4f}")
print(f" MAE: {eval_results['mae']:.4f}")
# 为用户0生成推荐
recommendations = mf.recommend_for_user(0, top_n=5)
print(f"\n为用户0的Top-5推荐:")
for j, (item_id, pred_rating) in enumerate(recommendations):
print(f" {j+1}. 物品{item_id}: 预测评分={pred_rating:.2f}")
# 比较结果
print(f"\n{'='*60}")
print("方法比较总结")
print('='*60)
for method in methods:
print(f"{method.upper()}: RMSE={results[method]['rmse']:.4f}, MAE={results[method]['mae']:.4f}")
# 可视化预测误差分布
plt.figure(figsize=(15, 5))
for idx, method in enumerate(methods, 1):
plt.subplot(1, len(methods), idx)
errors = np.array(results[method]['actuals']) - np.array(results[method]['predictions'])
plt.hist(errors, bins=30, alpha=0.7, edgecolor='black')
plt.xlabel('预测误差')
plt.ylabel('频率')
plt.title(f'{method.upper()}预测误差分布')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
def demonstrate_factorization_machine():
"""演示因子分解机"""
print("\n" + "="*60)
print("因子分解机演示")
print("="*60)
# 创建数据集
X, y, true_w0, true_w, true_v = create_fm_dataset(n_samples=2000, n_features=100)
print(f"数据集信息:")
print(f" 样本数: {X.shape[0]}")
print(f" 特征数: {X.shape[1]}")
print(f" 稀疏度: {(X.size - np.count_nonzero(X)) / X.size:.2%}")
# 划分训练集和测试集
split_idx = int(0.8 * len(X))
X_train, X_test = X[:split_idx], X[split_idx:]
y_train, y_test = y[:split_idx], y[split_idx:]
print(f"\n数据划分:")
print(f" 训练集大小: {len(X_train)}")
print(f" 测试集大小: {len(X_test)}")
# 训练因子分解机
print("\n训练因子分解机...")
fm = FactorizationMachine(n_factors=10, learning_rate=0.01,
reg_param=0.01, n_epochs=50, verbose=True)
fm.fit(X_train, y_train)
# 评估模型
eval_results = fm.evaluate(X_test, y_test)
print(f"\n因子分解机评估结果:")
print(f" RMSE: {eval_results['rmse']:.4f}")
print(f" MAE: {eval_results['mae']:.4f}")
# 与线性回归比较
from sklearn.linear_model import LinearRegression
print("\n与线性回归比较...")
# 训练线性回归
lr = LinearRegression()
lr.fit(X_train, y_train)
lr_predictions = lr.predict(X_test)
lr_mse = np.mean((y_test - lr_predictions) ** 2)
lr_rmse = np.sqrt(lr_mse)
lr_mae = np.mean(np.abs(y_test - lr_predictions))
print(f"线性回归评估结果:")
print(f" RMSE: {lr_rmse:.4f}")
print(f" MAE: {lr_mae:.4f}")
# 可视化比较
plt.figure(figsize=(10, 5))
# 预测值与真实值散点图
plt.subplot(1, 2, 1)
plt.scatter(y_test, eval_results['predictions'], alpha=0.5, label='FM预测')
plt.scatter(y_test, lr_predictions, alpha=0.5, label='LR预测', color='red')
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=2)
plt.xlabel('真实值')
plt.ylabel('预测值')
plt.title('预测值与真实值比较')
plt.legend()
plt.grid(True, alpha=0.3)
# 误差分布比较
plt.subplot(1, 2, 2)
fm_errors = np.abs(y_test - eval_results['predictions'])
lr_errors = np.abs(y_test - lr_predictions)
plt.boxplot([fm_errors, lr_errors], labels=['FM', 'LR'])
plt.ylabel('绝对误差')
plt.title('误差分布比较')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 分析特征重要性
print("\n特征重要性分析:")
feature_importance = np.abs(fm.w)
top_features = np.argsort(feature_importance)[-10:][::-1]
print("Top-10重要特征:")
for idx, feature_idx in enumerate(top_features):
print(f" {idx+1}. 特征{feature_idx}: 权重={fm.w[feature_idx]:.4f}")
def analyze_latent_factors():
"""分析潜在因子"""
print("\n" + "="*60)
print("潜在因子分析")
print("="*60)
# 创建数据集
ratings, true_ratings, true_user_factors, true_item_factors = create_movie_dataset()
# 训练矩阵分解模型
mf = MatrixFactorization(n_factors=5, learning_rate=0.01,
reg_param=0.02, n_epochs=100,
method='sgd', verbose=False)
mf.fit(ratings)
# 分析用户潜在因子
print("\n用户潜在因子分析:")
print(f"用户潜在因子矩阵形状: {mf.user_factors.shape}")
# 计算用户之间的相似度
user_similarity = np.dot(mf.user_factors, mf.user_factors.T)
# 找出最相似的用户对
n_users = mf.user_factors.shape[0]
similar_pairs = []
for i in range(n_users):
for j in range(i+1, n_users):
similar_pairs.append((i, j, user_similarity[i, j]))
similar_pairs.sort(key=lambda x: x[2], reverse=True)
print("\nTop-5最相似用户对:")
for i, j, sim in similar_pairs[:5]:
print(f" 用户{i}和用户{j}: 相似度={sim:.4f}")
# 分析物品潜在因子
print(f"\n物品潜在因子矩阵形状: {mf.item_factors.shape}")
# 计算物品之间的相似度
item_similarity = np.dot(mf.item_factors, mf.item_factors.T)
# 找出最相似的物品对
n_items = mf.item_factors.shape[0]
similar_item_pairs = []
for i in range(n_items):
for j in range(i+1, n_items):
similar_item_pairs.append((i, j, item_similarity[i, j]))
similar_item_pairs.sort(key=lambda x: x[2], reverse=True)
print("\nTop-5最相似物品对:")
for i, j, sim in similar_item_pairs[:5]:
print(f" 物品{i}和物品{j}: 相似度={sim:.4f}")
# 可视化潜在因子
plt.figure(figsize=(15, 5))
# 用户潜在因子可视化
plt.subplot(1, 3, 1)
# 使用PCA降维到2维以便可视化
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
user_factors_2d = pca.fit_transform(mf.user_factors)
plt.scatter(user_factors_2d[:, 0], user_factors_2d[:, 1], alpha=0.6)
plt.xlabel('潜在因子1')
plt.ylabel('潜在因子2')
plt.title('用户潜在因子分布')
plt.grid(True, alpha=0.3)
# 物品潜在因子可视化
plt.subplot(1, 3, 2)
item_factors_2d = pca.fit_transform(mf.item_factors)
plt.scatter(item_factors_2d[:, 0], item_factors_2d[:, 1], alpha=0.6, color='orange')
plt.xlabel('潜在因子1')
plt.ylabel('潜在因子2')
plt.title('物品潜在因子分布')
plt.grid(True, alpha=0.3)
# 用户-物品关系可视化
plt.subplot(1, 3, 3)
# 选择前几个用户和他们喜欢的物品
selected_users = [0, 1, 2]
colors = ['red', 'green', 'blue']
for idx, user_id in enumerate(selected_users):
# 获取用户喜欢的物品(评分>3)
liked_items = np.where(ratings[user_id] > 3)[0]
if len(liked_items) > 0:
# 获取这些物品的潜在因子
item_factors_selected = mf.item_factors[liked_items[:10]] # 取前10个
item_factors_2d_selected = pca.fit_transform(item_factors_selected)
# 绘制用户和物品
user_factor_2d = pca.transform(mf.user_factors[user_id].reshape(1, -1))
plt.scatter(user_factor_2d[:, 0], user_factor_2d[:, 1],
s=200, marker='*', color=colors[idx], label=f'用户{user_id}')
plt.scatter(item_factors_2d_selected[:, 0], item_factors_2d_selected[:, 1],
s=50, alpha=0.6, color=colors[idx])
plt.xlabel('潜在因子1')
plt.ylabel('潜在因子2')
plt.title('用户-物品关系')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
def practical_applications_and_considerations():
"""实际应用与注意事项"""
print("\n" + "="*60)
print("矩阵分解与因子分解机的实际应用")
print("="*60)
print("\n1. 超参数调优:")
print(" - 潜在因子数量k: 需要通过交叉验证选择,通常10-200")
print(" - 学习率: 太小收敛慢,太大会震荡,通常0.001-0.1")
print(" - 正则化参数: 防止过拟合,通常0.001-0.1")
print(" - 迭代次数: 通常50-500,配合早停策略")
print("\n2. 冷启动问题处理:")
print(" - 新用户: 使用人口统计特征或基于内容的特征")
print(" - 新物品: 使用物品内容特征或基于流行度的初始值")
print(" - 混合方法: 结合基于内容的推荐")
print("\n3. 增量学习:")
print(" - SGD天然支持增量学习")
print(" - ALS需要重新计算,但可以使用warm-start策略")
print(" - 在线学习: 使用小批量更新")
print("\n4. 模型解释性:")
print(" - 潜在因子难以直接解释")
print(" - 可以通过可视化或聚类来分析潜在因子")
print(" - 结合基于内容的方法提高解释性")
print("\n5. 计算优化:")
print(" - 并行计算: ALS容易并行化")
print(" - 分布式计算: 使用Spark MLlib等框架")
print(" - 近似计算: 使用负采样等技术")
print("\n6. 推荐多样性:")
print(" - 添加多样性正则化项")
print(" - 后处理: 对推荐结果进行重排")
print(" - 多目标优化: 平衡准确性和多样性")
print("\n7. 实际部署考虑:")
print(" - 实时性要求: 需要预计算或缓存")
print(" - 模型更新频率: 根据业务需求确定")
print(" - A/B测试: 验证模型效果")
print(" - 监控: 跟踪模型性能和业务指标")
def main():
"""主函数"""
print("="*60)
print("矩阵分解与因子分解机方法")
print("="*60)
# 1. 比较矩阵分解方法
compare_matrix_factorization_methods()
# 2. 演示因子分解机
demonstrate_factorization_machine()
# 3. 分析潜在因子
analyze_latent_factors()
# 4. 实际应用与注意事项
practical_applications_and_considerations()
# 5. 总结
print("\n" + "="*60)
print("总结与展望")
print("="*60)
print("\n矩阵分解方法的优势:")
print("1. 可扩展性好: 适合大规模数据")
print("2. 预测精度高: 在Netflix Prize等比赛中表现优异")
print("3. 灵活性高: 可以扩展为多种变体")
print("4. 内存效率高: 只需要存储低维矩阵")
print("\n因子分解机的优势:")
print("1. 通用性强: 可用于多种预测任务")
print("2. 处理高维稀疏数据: 特别适合推荐系统")
print("3. 特征组合自动学习: 无需手动设计特征交互")
print("4. 计算效率高: 线性时间复杂度")
print("\n发展趋势:")
print("1. 深度学习结合: 如神经矩阵分解")
print("2. 序列建模: 考虑用户行为序列")
print("3. 多模态融合: 结合文本、图像等多种信息")
print("4. 可解释性增强: 提高模型透明度")
print("5. 自动化机器学习: 自动调参和特征工程")
print("\n学习建议:")
print("1. 理解数学原理: 特别是优化方法和正则化")
print("2. 动手实践: 在不同数据集上尝试")
print("3. 阅读经典论文: 如Koren的矩阵分解论文")
print("4. 参与竞赛: 如Kaggle上的推荐系统比赛")
print("5. 关注最新进展: 如深度学习推荐模型")
if __name__ == "__main__":
main()六、总结与展望
1. 矩阵分解方法总结
矩阵分解作为协同过滤的重要扩展,通过将用户和物品映射到低维潜在空间,有效解决了基于记忆的协同过滤面临的可扩展性和数据稀疏性问题。从基础的SVD到SVD++,矩阵分解方法不断演进,加入了偏置项、隐式反馈等元素,提高了预测精度。
关键要点:
-
潜在因子:矩阵分解的核心是学习用户和物品的潜在特征表示
-
优化方法:SGD和ALS是两种主要的优化算法,各有优缺点
-
正则化:L2正则化防止过拟合,是模型泛化的关键
-
偏置建模:用户偏置和物品偏置能显著提高预测精度
2. 因子分解机总结
因子分解机作为一种通用预测模型,特别适合处理高维稀疏数据,如推荐系统中的特征数据。FM通过特征交互的因子化,能够学习特征之间的二阶交互关系,且计算效率高。
关键要点:
-
特征交互:FM自动学习特征之间的交互关系
-
计算优化:通过数学变换将计算复杂度从O(n²)降到O(kn)
-
泛化能力:即使特征组合未出现在训练数据中,也能进行预测
-
扩展性:可以扩展到FFM、高阶FM等变体
3. 实践建议
在实际应用中,选择矩阵分解还是因子分解机需要考虑以下因素:
-
数据类型:
-
如果只有用户-物品交互数据,矩阵分解更合适
-
如果有丰富的特征数据,因子分解机更合适
-
-
计算资源:
-
矩阵分解更适合大规模用户-物品矩阵
-
因子分解机更适合高维特征数据
-
-
业务需求:
-
如果只需要评分预测,两者都适用
-
如果需要结合多种特征,因子分解机更灵活
-
-
实施复杂度:
-
矩阵分解实现相对简单
-
因子分解机需要特征工程,但功能更强大
-
4. 未来发展方向
随着深度学习的发展,矩阵分解和因子分解机也在不断演进:
-
神经矩阵分解(Neural MF):将矩阵分解与神经网络结合
-
深度因子分解机(DeepFM):结合FM和深度神经网络
-
图神经网络:将用户-物品交互看作二部图,使用图神经网络建模
-
自注意力机制:用于序列推荐和特征交互建模
-
多任务学习:同时优化多个相关任务
 矩阵分解与因子分解机详解
矩阵分解与因子分解机详解
























 3466
3466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










