视觉计算导论课程作业2洛伦兹吸引子
蒂姆•莫里斯
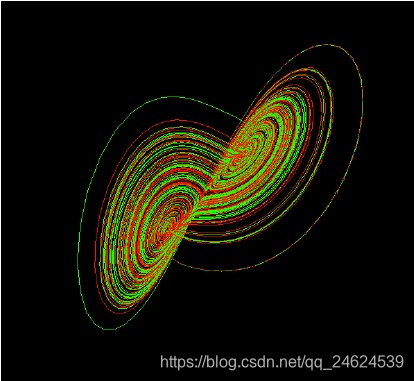

介绍
这个实验室关注的是在屏幕上创建洛伦兹吸引子,它由以下方程定义,确定在给定时间点的速度的x, y, z分量:
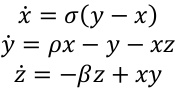
s r和b都是常数。它们的合理值是s = 10.0, r = 28.0和b = 2.6
为了画出吸引子,你必须从某个x y z点开始。将x, y, z的值代入上述方程,以及所选的s, r和b的值。方程计算这个位置点的瞬时速度。这必须被积分得到下一个点的位置。这很容易实现,通过将每个速度分量乘以一个时间,并添加之前的位置:
![]()
y和z也是一样,新位置变成了下一次迭代的当前位置。
你所编写的代码将实现这两个粒子的运动,它们必须开始时离彼此很近,但不是在同一个地方。粒子会留下痕迹。
开始
按照实验室1讲义的入门部分的说明来获得基本的、空白的网页。如果你剪切和粘贴,那么不要忘记引号,长行被包装和连字符的问题。
当你想改变相机的视图的吸引器(通过点击和拖动),你将需要一些额外的库,添加以下导入立即在现有的一个。
import { OrbitControls } from
"https://web.cs.manchester.ac.uk/three/three.js- master/examples/jsm/controls/OrbitControls.js";
不要忘记换行。
变量和函数
你需要像之前一样为摄像机、场景和渲染器设置变量,并为orbitcontrol添加一个额外的变量:controls。
你还需要变量来表示你将要绘制的吸引器。我们将在下一节中讨论这些。所有这些变量都可以设置为全局变量,以简化编程。
你需要一些函数来初始化模拟(你可以调用init())并制作动画(你可以调用animate())。在声明了全局变量之后,这些变量将立即被调用,这与Lab1中相同。下面将讨论每个函数的主体。
洛伦茨变量
您将需要一个常数来定义点数的极限。为什么你需要一个限制?当达到这个极限时会发生什么?因此,您需要一个变量来维护已绘制的点数的计数。
你应该使用一个常量来定义你想要绘制的吸引器的数量。这将更容易改变吸引子的数量。然后下面的每个变量都是这样大小的数组,每个元素都指向一个不同的吸引子。
在向吸引器添加新点时,是否想绘制一个更大的点?如果你这样做了,你将需要定义一个在每一帧的吸引器头部绘制的球体。所以需要一个球体对象数组。
你需要变量来存储线和球体的几何和材质属性(四个变量,它们将是数组)。还有两个变量来聚合各自的几何形状和材料(再次是数组),你将添加到场景中。
你需要一个数组来存储吸引器的颜色(以及球体,如果你想让它们的颜色与线条不同的话)。
你将用一系列的点来表示每个吸引器,你需要存储所有的点吗?答案是肯定的:考虑一下刷新屏幕时会发生什么。因此,您需要一个数据结构来存储每个吸引器上点的坐标。这个结构也将被添加到线的几何结构中。
吸引子的最新点将存储在动画的每次迭代。你需要为每个点设置一个x, y, z坐标(如果你想拥有多个吸引器,x, y, z可以是数组)。
s, r, b -洛伦兹常数与上面提到的值:10.0,28.0和2.6(小数点和0很重要)。这对所有的吸引子都是一样的。
一个常数时间步长,来表示方程中的Dt。0.01是一个敏感值。一个变量,用来记录已经画了多少个点。
变量如何初始化将在下一节中描述。
初始化
你需要初始化场景,相机和渲染器。这与在Lab1中是一样的,除了你将相机放置在(0,0,1000)。
你需要初始化orbitcontrols
(https://threejs.org/docs/index.html#examples/en/controls/OrbitControls) by: controls = new OrbitControls(camera, renderer.domElement); controls.autoRotate = true;
你需要初始化吸引器的起始点。没有两个吸引子具有相同的起点,为什么?x、y和z坐标的合理值都在距离原点0.02范围内。
你还需要初始化线条的颜色(如果你想让它们是不同的颜色,你还需要初始化球体)。
初始化函数的其余部分与设置Lorenz变量有关。您可能需要一个循环来处理数组变量。在循环中有三个任务要执行。
1.创建线几何体。
2.创建线条材质。
3.将几何体和材料组合成一个对象并添加到场景中。
4.在吸引器的头部为球体创建几何图形。
5.在吸引器的头部为球体创建材质。
6.将几何体和材料组合成一个对象并添加到场景中。
线几何
线几何图形被构造为BufferGeometry,例如。
LorenzGeometry = new THREE.BufferGeometry();
https://threejs.org/docs/index.html#api/en/core/BufferGeometry
然后你需要创建一个数组来保存这些点的坐标,例如。
line = new Float32Array(…);
这个数组应该有多少个元素长?(记住你有一个最大数量的点,每个点有三个坐标。)
然后将其作为属性添加到线几何体中:
LorenzGeometry.setAttribute(‘position’, new
THREE.BufferAttribute(line, 3));
https://threejs.org/docs/index.html#api/en/core/BufferAttribute
这个链接定义了如何在缓冲区中存储数据。简单地说,缓冲区是一个一维数组,所以如果我们想在其中存储三维坐标,我们将在连续的条目中有x、y、z值。
线材料
吸引子的材料是由以下元素构成的一条基本线:
LorenzMaterial = new THREE.LineBasicMaterial({color: ???, linewidth: 1})
? ?指示您应该定义一个有效的颜色值。它将是一个24位十六进制数字,例如0x0000FF = blue.
https://threejs.org/docs/index.html#api/en/materials/LineBasicMaterial
在场景中添加这一行
这类似于在Lab1中将立方体添加到场景中的方法。
line = new THREE.Line(LorenzGeometry, LorenzMaterial); scene.add(line);
球面几何
球体可以这样构造:
sphereGeometry = new THREE.SphereGeometry( ??? )参数定义在
https://threejs.org/docs/index.html#api/en/geometries/SphereGeometry
球材料
材质是一个基本的网格:
sphereMaterial = new THREE.MeshBasicMaterial({color: ??? });颜色定义如上所述。
https://threejs.org/docs/index.html#api/en/materials/MeshBasicMaterial
将球体添加到场景中
如上所述,在添加到场景之前,我们必须将材质和几何体组合成一个单一的对象。代码和上面一样(当然,变量不同),除了你是在构建一个网格而不是一条线。
动画
|
动画函数可以被称为animate()(只是要确保它与requestAnimationFrame()的参数同名,因为该函数定义了在渲染帧时要调用什么)。它应该调用一个函数来更新Lorenz点,否则它的主体几乎与Lab1相同: |
function animate() {
requestAnimationFrame(animate);
updateLorenz(); // add a new point to each Attractor renderer.render(scene, camera);
} // animate()
这个函数应该检查的另一件事(这里没有说明)是,已经绘制的点数小于可以存储的最大点数。如果这个测试失败了,你该怎么办?
updateLorenz ()
这个函数为每个吸引器计算新点的坐标,并将它们添加到前面定义的变量line中。它也将在新的位置绘制一个球体。
对每个吸引子执行的操作为:
1.计算x、y和z坐标的增量。
2.更新x, y和z坐标。
3.更新球体的位置。
4.将新的点添加到点数组(初始化中的行)。
5.定义要绘制的点的范围并绘制它们。
并且只增加一次计数点数。
计算到x, y, z的增量
更新x, y, z
这是通过引言中的方程实现的。
更新球体的位置
Mesh类有一个名为position的成员。它有成员x, y和z。这些应该用新计算的位置进行更新。
将新点添加到点数组中
您已经定义了一个用于存储这些点的缓冲区。它是一个一维数组,因此x、y、z值必须存储在连续的位置。
定义要绘制的点的范围并绘制它们
line有一个名为geometry的属性,它有一个成员函数setDrawRange。用它来定义要渲染的第一个和最后一个点。
https://threejs.org/docs/index.html#api/en/core/BufferGeometry.setDrawRange
最后通过设置属性实现绘图
line.geometry.attributes.position.needsUpdate为true。
如果你用这种方式来画,你会发现窗口中的吸引器非常小。因此,当您将x、y和z值分配给任何其他变量时,您可以将它们缩放为合适的数字。一个合适的尺度值是10.0,在这个函数中把它作为一个局部变量。
重置
当绘制的点数超过可以存储的点数时,可能需要重置一些变量。哪一个?以及如何?您可以添加代码来将其重置为animate(),或者将其编写为一个从animate()调用的独立函数。
查询
1. 为什么你需要限制点的数量?
点数越多,数组需要存储的总的点数也会更多(倍数增长的),占用更多的内存资源。
2.当达到这个极限时会发生什么?
网页上的画清除,数组里面的数据清除,重新开始计算,并画出动画来。
3.为什么要把吸引器的头画成一个更大的点?
因为随着时间的增加,屏幕上的曲线会越来越长,如果吸引器的头很小的话,就会看不清吸引器变化的位置。
4.当屏幕刷新时,“旧”数据会发生什么变化?
刷新时,随着时间的增长,旧的数据会被新计算得到的数据替换掉。
5.为什么两个吸引子不能有相同的起点?
保证吸引子变化的路径是不一样的,如果是相同的起点,屏幕上只能看到一个吸引子和一条曲线。
6.存储点坐标的缓冲区有多长?
MAXPOINTS= 5000000
7.球面几何(Sphere Geomentry)的参数是什么?
radius=3, widthSegments=45, heightSegments=45
8.如果(当)要绘制的点的数量超过了点缓冲区的容量,你做了什么?
将当前点数置零(drawCount = 0),将所有吸引子的坐标重置为初始值。
9.哪些变量必须重置?值是什么(to what value)?
当前点数置零和所有吸引子的坐标重置为初始值。
drawCount = 0;
x[0] = 0.1;
y[0] = 0;
z[0] = 0.2;
x[1] = 0;
y[1] = 0.1;
z[1] = 0;
10.改变s的影响是什么?
s越小所有的吸引子越收敛到同一点,演化速度越慢;s越大混沌蝴蝶效应越明显。
11.改变r的影响是什么?
r越小,所有的吸引子越逐渐收敛到同一点;r越大,吸引子越排斥,轨迹越复杂,吸引子倾向于不再交叉。
12.改变b的影响是什么?
b越小所有的吸引子越收敛到同一点,演化速度越慢;b越大蝴蝶混沌效应越明显,演化速度越快。
13.增加时间步长dt的影响是什么?
加快了演化速度,点的坐标值也会更大,太大的步长会导致无法正常显示混沌蝴蝶。
14.你需要修改什么来增加吸引子的数量?
修改NUM_LORENZ的值,增加LorenzColours和SphereColours的表示颜色的数组长度,增加x,y,z表示吸引子初始坐标的长度。
提交
准备一份文档,将你的答案保存为pdf格式。把你的代码和这个文件压缩,并把它提交到黑板上的适当位置
评分方案
| 问题1 | 1马克 |
| 问题2 | 1马克 |
| 问题3 | 1马克 |
| 问题4 | 2标志 |
| 问题5 | 2标志 |
| 问题6 | 2标志 |
| 问题7 | 2标志 |
| 问题8 | 1马克 |
| 问题9 | 2标志 |
| 问题10 | 1马克 |
| 问题11 | 1马克 |
| 问题12 | 1马克 |
| 问题13 | 2标志 |
| 问题14 | 1马克 |
|
|
|
| 总计 | 20个标志 |
























 1801
1801

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










