计算机图形学入门08：反走样、滤波与卷积

1.抗锯齿(反走样)

        在上一章中，在光栅化三角形的时候出现了明显的锯齿效果。如下图所示是三角形采样过程：

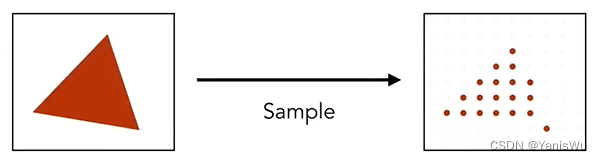
        从图上可知像素点不是纯红色就是纯白色。如果在采样前先进行模糊操作(滤波)，如下图所示：

        经过模糊操作后三角形的边缘颜色变化有了一定的过渡，再进行采样时，靠近三角形边缘的地方可以采到一部分过渡色的像素，采样结果不在是要么红色要么白色，就可以达到抗锯齿的目的。

        通过下面两张图来看使用模糊操作后的效果对比。

        再来看另外一组通过滤波处理再采样的效果。

        综上，在进行采样之前先进行模糊操作(滤波)，能够达到明显的抗锯齿效果。

2.频域与时域

        上面提到通过先进行滤波操作，再采样来达到抗锯齿的效果，叫做Blurred Aliasing。那么先进行采样，再进行滤波操作能不能同样达到抗锯齿的效果呢，答案是不行的。看下面两张图对比一下，第一张先进行采样再进行滤波操作，第二张是先进行滤波操作再进行采样，可以发现第一种操作是行不通的。

        这是为什么呢？这里需要引入频域(Frequency Domain)和时域(Spatial Domain)的概念。

        频域用来表示不同频率下信号的变化，用横轴表示频率,纵轴是该频率信号的幅度,也就是通常说的频谱图。

        时域用来表示不同时间下信号的变化，也可以表示空间上信息。用横轴表示时间,纵轴是当前时间信号的幅度。

2.1周期与频率

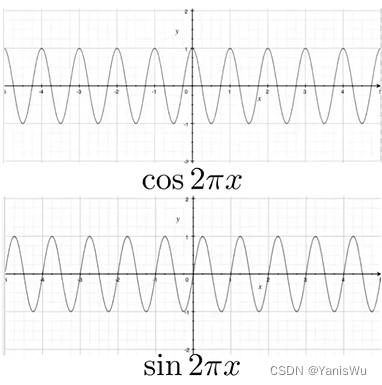
        下图是周期性变换的波形函数正弦和余弦函数，它们之间的不同点在于它们的相位不同。

        那么使用余弦与正弦函数有啥好处呢？这里用余弦函数举例子，如下图所示：

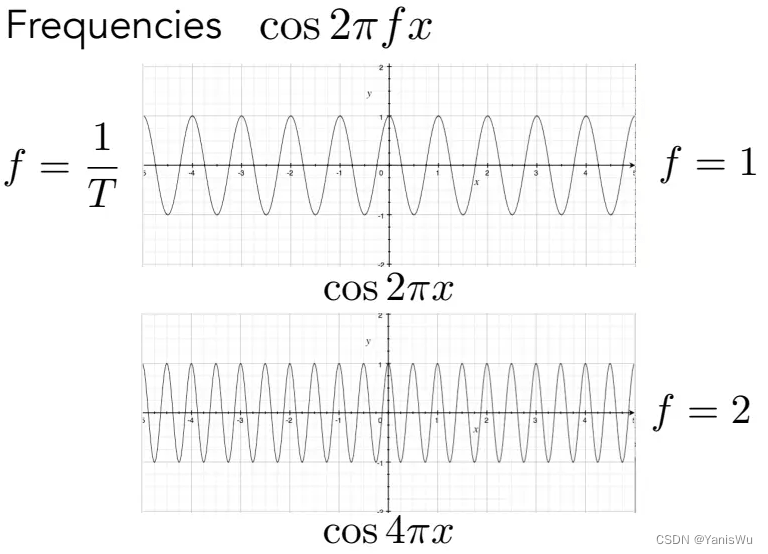
        通过余弦函数x前面的系数，会得到不同的余弦波，代表频率不同。f代表频率，频率越大代表余弦波变化越快，周期(T)越短。对于图像信号而言，我们认为两个像素间的颜色变化大则代表频率高，反之则是频率低。

2.2傅里叶变换

2.2.1傅里叶级数展开

        任何周期函数都可以用一系列正弦、余弦函数构成的线性组合以及一个常数项来表示，这种展开方式我们称为傅里叶级数展开。

        如果需要获取一个函数得到向下面这样周期变换