- Perceptron Hypothesis Set
对于银行是否发送信用卡的问题,把每位顾客的年龄、年收入等特征看成一个向量 x=(x1,x2,...xd) ,计算顾客每个特征与权重的乘积之和,如果结果大于某个阈值(threshold),那么就发送信用卡,否则不发送信用卡。
根据以上的信息,我们就可以得到一个线性形式的 h ,它属于假设集合H 。其中 sign(⋅) 是符号函数:
h(x)=sign((∑i=1dwixi)−threshold)
仔细观察上面的式子,我们发现可以把最后的 −threshold 当做 w0 ,令 x0=+1 ,那么 h(x) 就可以转化成如下的向量形式:
感知机是一个二元(线性)分类器,其几何表示为:在二维空间内表现为一条直线,三维空间内表现为平面,更高维的空间则表现为超平面。 Perceptron Learning Algorithm(PLA)
根据第一节的内容,我们可以找到超平面 w 将数据分为两部分,但是符合条件的超平面 wi 有很多个,那么我们如何找到最合适的超平面呢?
我们可以这样来做:首先随机选取一个超平面 wt ,找到一个在当前被错误分类的点 (xn(t),yn(t)) ,然后根据这个点去修正当前的超平面 wt ,得到一个新的超平 wt+1 ,重复这项工作直到没有被错误分类的点为止,最后得到的超平面就是我们所要的。这就是感知机学习算法(PLA)。算法更详细的流程如下图所示,其中点的遍历顺序可以是随机的,也可以是按照某个特定顺序:
可以看出,当超平面不再犯错误的时候算法会停止。但是我们不能保证迭代多轮之后,算法一定能收敛,也就是说不能保证算法一定能停止。下面我们讨论PLA的收敛性。Guarantee of PLA
PLA的目的是找到一个将所有数据正确分类的超平面,如果数据集本身不是线性可分的,那么PLA就不会收敛。所以PLA能够收敛的充要条件是数据集线性可分。
当数据集线性可分的时候,一定会存在一个完美地 wf 对于所有的 xn 使得 yn=sign(wTfxn) 。由于 wf 是使得所有点都正确分类的一个超平面,那么每个点 xn 与 wf 这个超平面的距离和 yn 的乘积一定是正数,所以有如下公式:
yn(t)wTfxn(t)≥minnyn(t)wTfxn(t)>0
当用 (xn(t),yn(t)) 去更新 wt 时, wTf⋅wt 会逐渐增大:
wTf⋅wt=wTf(wt−1+yn(t−1)xn(t−1))≥wTfwt−1+minnyn(t−1)wTfxn(t−1)>wTfwt−1+0
注意,只有当 wt−1 出现错误的时候我们才进行更新,如果出现分类错误,那么就有 sign(wTt−1xn(t−1))≠yn(t−1) ,即 yn(t−1)wTt−1xn(t−1)≤0 。由于这个原因, ∥wt∥2 才会增长的比较缓慢,具体推导如下:
∥wt∥2=∥∥wt−1+yn(t−1)xn(t−1)∥∥2=∥wt−1∥2+2yn(t−1)wTt−1xn(t−1)+∥∥yn(t−1)xn(t−1)∥∥2≤∥wt−1∥2+0+∥∥xn(t−1)∥∥2≤∥wt−1∥2+maxn∥xn∥2≤∥wt−2∥2+2⋅maxn∥xn∥2≤...≤t⋅maxn∥xn∥2
由于 yn(t−1) 只有 1 和−1 两个值,平方之后没有区别,所以在后面的推导中就省略掉了。根据上面的推导,我们看出 ∥wt∥ 每次增加的值不超过整个数据集空间的半径,所以 wTf⋅wt 增加的原因不是因为 wt 的长度,而是因为两个向量之间的夹角变小了。
根据上面的推导结果,可以得出如下结论:
t⋅minnyn(t−1)wTfxn(t−1)≤wTf⋅wt≤∥∥wTf∥∥⋅∥wt∥≤t√⋅maxn∥∥xn(t−1)∥∥t⋅minnyn(t−1)wTfxn(t−1)≤t√⋅maxn∥xn∥
令 γ=minn(ynwTfxn) , R=maxn∥xn∥ ,则上式可以写成:
tγ≤t√Rt2γ2≤tR2
所以
t≤(Rγ)2
上式表明,错误分类的次数 t 是有上界的,经过有限次迭代可以找到将训练数据完全分开的超平面。也就是说,当训练数据线性可分时,PLA是收敛的。- Non-Separable Data
PLA非常简洁,较少的代码量就可以实现,而且可以运行在任意维度上。但是它也有明显的缺点。首先,我们“假设”数据集是线性可分的,但是我们如何证明数据集真的是线性可分的呢?其次,我们只证明了PLA会收敛,但是它什么时候收敛?R 可以轻易地求出来,但是 γ 是由 wf 计算出来的,而我们并不知道 wf 的值,假如我们知道 wf ,那还需要机器学习干什么呢?:-P
如果数据集真的是线性不可分的,那么我们假定数据集中有一些噪点,允许算法有一定的错误,我们的目标是使得被错误分类的点最少,即:
wg←argminw∑n=1N[yn≠sign(wTxn)]
这是一个NP-Hard问题,只能在多项式时间内找到近似解。下面介绍Pocket Algorithm就是一个利用贪心策略找出近似解的算法。具体如下图所示:
它和PLA的区别是只有当 wt 优于 wt−1 ,即当 wt 犯的分类错误比 wt−1 少时,才更新 wt 。
《机器学习基石》课程笔记(2)
最新推荐文章于 2020-03-01 17:22:46 发布








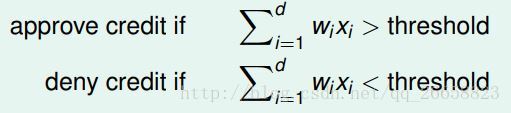
















 7327
7327











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








