设计一个有 getMin功能的栈_c++中getmin-CSDN博客

本文介绍了一种特殊栈的设计，该栈除了基本功能外还能在O(1)时间内获取最小元素。通过使用两个栈——一个存储数据，另一个跟踪最小值，并提出了两种不同的实现方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

该题目来自《程序员代码面试指南》，在理解其实现原理的基础上，将Java实现改用C++实现。

题目

实现一个特殊的栈，在实现栈的基本功能的基础上，再实现返回栈中最小元素的操作。

要求

pop、push、getMin操作的时间复杂度都是O(1) 。
设计的栈类型可以使用现成的栈结构。

难度

解答

在设计上我们使用两个栈，一个栈用来保存当前栈的元素，其功能和一个正常的栈没有区别，这个栈即为stackData，另一栈用于保存每一步的最小值，这个栈记为stackMin。具体的实现方式有两种。

第一种实现方案为：

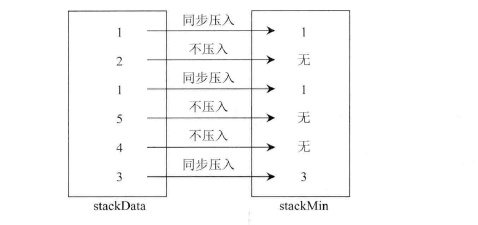
压入数据规则

假设当前数据为newNum，先将其压入stackData。然后判断stackMin是否为空：

- 如果为空，则newNum也压入stackMin
- 如果不为空，则比较newNum和stackMin中栈顶的元素的大小：
  - 如果newNum更小或两者相等，则newNum也压入stackMin。
  - 如果stackMin栈顶元素更小，则stackMin不压入任何内容。

弹出规则

先在stackData中弹出栈顶元素，记为value。然后比较当前stackMin的栈顶元素和value哪一个更小。通过上面的压入规则可知，stackMin中存在的元素是从栈底到栈顶逐渐变小的，stackMin栈顶的元素既是stackData栈中最小的元素，也是stackMin栈中最小的元素。

因此，当value等于stackMin栈顶元素时，stackMin栈也弹出栈顶元素。当stackMin栈顶元素小于value值时，stackMin不弹出栈顶元素。最后返回value。可以看出，压入规则和弹出规则是对应的。

查询当前栈中的最小值操作

由上文可以，stackMin栈顶元素始终是当前stackData栈的最小元素。因此查询stackMin栈顶元素即可知道当前栈中的最小元素。

public class MinStack1{

    private Stack<Integer> stackData;
    private Stack<Integer> stackMin;

    public MinStack1(){
        stackData = new Stack<Integer>();
        stackMin = new Stack<Integer>();
    }

    public void push(int newNum){
        if (stackMin.isEmpty()) {
            stackMin.push(newNum);
        }else if (newNum <= getMin()) {
            stackMin.push(newNum);
        }
        stackData.push(newNum);
    }

    public int pop(){
        if (stackData.isEmpty()) {
            throw new RuntimeException("Your stack is empty!");
        }
        int value = stackData.pop();
        if (value == getMin()) {
            stackMin.pop();
        }
        return value;
    }

    public int getMin() {
        if (stackMin.isEmpty()) {
	    throw new RuntimeException("Your stack is empty!");
        }
        return stackMin.peek();
    }                                               
}

class MyStack1 //C++实现
{
private:
	stack<int> stackData;
	stack<int> stackMin;
public:
	MyStack1(){}
	void push1(int numNum);
	int pop1();
	int getmin();
};

void MyStack1::push1(int newNum)
{
	if(stackMin.empty())
		stackMin.push(newNum);
	else if(newNum <= getmin())
		stackMin.push(newNum);
	stackData.push(newNum);
}
int MyStack1::pop1()
{
	if(stackData.empty())
	{
		cout<<"your stack is empty.";
		return -1;
	}
	int value = stackData.top();  //由于c++中pop函数的返回类型为void，因此不能采用Java中的描述实现。
	stackData.pop();
	if(value == getmin())
		stackMin.pop();
	return value;
}
int MyStack1::getmin()
{
	if(stackMin.empty())
	{
		cout<<"your stack is empty";
		return -1;
	}
	return stackMin.top();
}

class MinStack {  //LeetCode下该问题的优质回答。结合上面正确的逻辑，这个代码实现地非常简洁清晰。
private:
    stack<int> s1;
    stack<int> s2;
public:
    void push(int x) {
	    s1.push(x);
	    if (s2.empty() || x <= getMin())  s2.push(x);	    
    }
    void pop() {
	    if (s1.top() == getMin())  s2.pop();
	    s1.pop();
    }
    int top() {
	    return s1.top();
    }
    int getMin() {
	    return s2.top();
    }
};

第二种设计方案的思路这里简单的介绍一下：

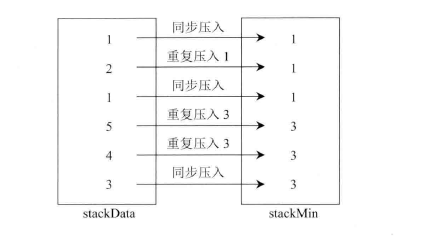
假设当前数据为newNum，先将其压入stackData。然后判断stackMin是否为空：

- 如果为空，则newNum也压入stackMin。如果不为空，则比较newNum和stackMin中栈顶的元素的大小：
  - 如果newNum更小或两者相等，则newNum也压入stackMin中。
  - 如果stackMin栈顶元素更小，则把stackMin栈顶元素重复地压入stackMin中。

public class MinStack2 {

    private Stack<Integer> stackData;
    private Stack<Integer> stackMin;

    public MinStack(){
        stackData = new Stack<Integer>();
        stackMin = new Stack<Integer>();
    }

    public void push(int newNum){
        if (stackMin.isEmpty()) {
            stackMin.push(newNum);
        }
        else if (newNum <= getMin()) {
            stackMin.push(newNum);
        }else {
            stackMin.push(getMin());
        }
        stackData.push(newNum);
    }

    public int pop(){
        if (stackData.isEmpty()) {      
            throw new RuntimeException("Your stack is empty!");
		} 
		int value = stackData.pop();
		stackMin.pop(); 
		return value; 
	} 
	public int getMin(){ 
		if (stackMin.isEmpty()) { 
			throw new RuntimeException("Your stack is empty!");
		}
		return stackMin.peek(); 
	}
}

方案一和方案二都是使用stackMin栈保存着stackData每一步的最小值。共同点是所有操作的时间复杂度为O(1)，空间复杂度为O(n)。

参考链接 LeetCode上对应问题

学习书籍《程序员代码面试指南》