Towards Causality-Aware Inferring: A Sequential Discriminative Approach for Medical Diagnosis翻译

摘要

医疗诊断助手（MDA）旨在建立一种交互式诊断agent，以依次询问与疾病诊断相关的症状。但是，由于用于构建患者模拟器的对话记录是被动收集的，因此存在一些任务无关的偏差（例如收集者的偏好）可能会破坏数据质量。这些偏差可能会阻碍诊断agent从模拟器中获取可迁移的知识。这项工作试图通过利用因果图来识别和解决两个代表性的因果无关偏差，即，（i）default-answer bias和（ii）distributional inquiry bias，从而解决MDA中的这些关键问题。具体而言，偏差（i）源自患者模拟器，该模拟器试图以一些有偏差的默认答案来回答未记录的问题。因此，由于有偏差的答案，诊断agent无法完全证明其具有的优势。为了消除这种偏差，并受到使用因果图的倾向评分匹配技术的启发，我们提出了一个基于倾向的患者模拟器，以通过从其他记录中获取知识来有效地回答未记录的问题；偏差（ii）本质上与被动收集的数据一起出现，其是训练agent “如何学习”而不是“如何记住”的关键障碍之一。例如，在训练数据的分布中，如果一个症状与某种疾病高度耦合，则agent可能会学会仅询问该症状以区分该疾病，这种知识可能无法推广到分布之外的疾病。为此，我们提出了一种渐进保证agent，其包括分别考虑症状询问和疾病诊断的双重过程。询问过程由自上而下的诊断过程驱动，以增强诊断置信度。诊断过程在精神和概率上描绘了患者，并进一步通过干预以使用精神表示进行推理。以这种合作的方式，我们提出的agent学习推理后询问，而不是遵循训练数据的询问模式。广泛的实验表明，我们的框架实现了新的最优性能，并具有可迁移能力的优势。

1.介绍

　　医疗诊断助手（MDA）的目的是学习一种能够与患者依次相互的agent，以收集症状信息，并进行初步诊断。
　　由于巨大的工业潜力，MDA任务吸引了越来越多研究人员的关注。类似于其他面向任务的对话，例如电影票/餐厅预订，在线购物和技术支持，MDA由用户与agent之间的一系列基于对话的交互组成，可以作为马尔可夫决策过程，并通过深度强化学习（RL）解决。但是，与RL agent在视频游戏和棋盘游戏上进行试错任务不同，许多现实世界中的任务（例如MDA）只能在现实世界场景被动收集观测数据，例如患者和医生之间的诊断对话记录。因此，为了将RL应用于MDA，使用现实世界中收集的被动观测数据构建模拟器被认为是一种有前途的解决方案。不幸的是，这些被动观测数据不可避免地存在因果和任务无关的因素（例如收集者偏好和患者分布）。在不缓解这些偏差的情况下学习RL agent会阻碍其发现数据背后的因果和可迁移知识。
　　在本文中，我们从被动数据使用和诊断agent设计的角度发现了两个代表性的因果无关偏差。根据这些偏差的来源，我们分别将它们表示为default-answer bias和distributional inquiry bias。
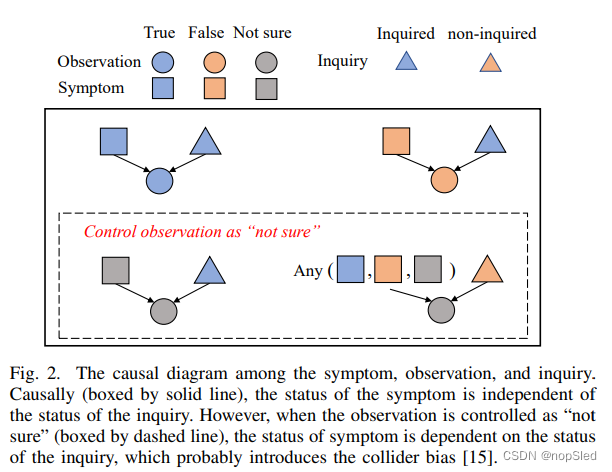
　　Default-answer bias。在大多数任务的数据清理过程中，设置默认值是解决缺失值问题的常见方案。在MDA中，先前的方法同样使用了对未记录的症状问题采用默认答案的患者模拟器。具体来说，为了模拟患者，模拟器从对话数据集中选择一个对话记录（即锚记录），然后通过查看锚记录中的询问项来回答agent的问题。但是，由于记录仅反映了真实世界的一个方面（即事实方面），因此基于该事实数据的模拟器可能无法回答RL agent的未被记录的询问（即反事实方面），如图1所示。为了处理反事实问题，先前的工作只会使用“不确定”作为模拟器的默认答案。然而，由于观测内容（即答案）是agent询问患者所具有症状的常见原因，事实上默认答案策略会带来对撞偏差，这在由症状，问题，答案组成的因果图（CD）上进行了展示。在图2中，因果图显示在实心框中，症状的状态和询问状态是无关的。但是，在虚线框中，当询问观测被控制为“不确定”时，症状的状态仅减少到一个候选，即“不确定”。因此，控制非询问观测会引入症状与询问之间的非因果关系。直观地，使用默认答案的模拟器假设，如果未询问患者症状，则患者应该无法确定这种症状，这可能会偏离现实。学习具有这种偏差会阻碍agent获得症状与疾病之间的因果关系。不幸的是，无法通过增加更多训练数据来消除这种偏差。更糟糕的是，由于MDA信息的稀疏性，在训练阶段模拟器会被频繁询问这种未被记录的症状，这进一步扩大了对偏差所带来的负面影响。在具有严重的对撞偏差的模拟器下进行训练和评估不能完全反映诊断agent的优势。
　　事实上，模拟器应推断出询问的不在记录中的症状，并相应地给出答案，而不是提供默认答案。为了提供这种“无知性”，我们基于潜在输出框架（PO）通过利用众所周知的因果推理技术（Propensity Score Matching (PSM)）提出了基于倾向的患者模拟器（PBP）。我们提出的模拟器迈出了新的一步，将CD和PO框架的不同因果关系概念结合在一起，以解决实际问题。通常，由于未观察到的因素，例如个体效应，因此在MDA等现实世界任务中，完整的CD是未知的。 PO允许我们的模拟器执行因果推断，重点关注由部分CD揭示的特定问题。具体来说，对于在MDA中构建的PBP，我们首先基于被动收集数据的部分CD识别对撞点（见图2）。接下来，我们使用PSM根据其症状和疾病标签来计算每个记录的倾向评分，然后以相似的倾向得分进行分组。由于除了对撞点外，症状和疾病是匹配的，因此对撞点在分组记录中是进行反控制的。因此，这些记录中未观察到症状的潜在存在性显着降低了对撞偏差。
　　Distributional inquiry bias。由被动收集数据带来的另一个代表性偏差是分布偏差，这也是训练agent“如何学习”而不是“如何记住”的关键障碍之一。由于收集MDA数据的困难和高成本，诊断agent的训练数据量有限，并且可能对OOD数据表现较差。具体而言，我们发现数据的分布偏差可能通过诊断agent的询问行为流入疾病诊断，我们将这种偏差称为分布询问偏差，如图4a所示。需要注意的是，诊断agent对用于最终判别诊断的一系列症状进行询问。询问行为就像一个窗口，可以控制患者到最终诊断的信息量。而且，当学习信息不全面时，例如，疾病与少量症状相结合时，agent可能很难将这些不常见的症状与该疾病关联。因此，一旦症状询问的要求改变了（例如，改变患者的分布），agent可能无法迁移知识来处理这些情况。
　　为此，我们根据图4a提出了一种渐进保证agent（P2A）。P2A是双重过程，由两个独立但需合作的分支组成，即诊断分支和询问分支。如图3所示，以二分类案例为例，根据历史观察（即图中的$s_t$），诊断分支通过干预患者的未知方面，来进行推理和计划。这种干预导致多种虚构的未来场景。然后，这些虚构的轨迹被诊断为不同的疾病簇（橙色或绿色）。一旦一个类簇的数目远远超过了另一个类簇的决策阈值，agent将停止询问，同时通知该类簇对应的疾病。与先前的通过黑盒策略网络来停止询问过程的工作不同，我们的P2A的停止机制更可靠且可解释。特别是，不同类簇与我们P2A决策阈值概念之间的竞争行为均来自神经科学中的扩散模型。我们的P2A不局限于神经科学中的二分类案例，因此从计算角度将扩散模型扩展到多分类设置。通过干预，我们的P2A中的诊断决定不仅是根据受分布询问行为影响的历史观察结果做出的，而且还取决于想象中的已完成的患者信息。如图4b所示，我们的P2A通过将其原因减少到患者的结果中，从而干预了非询问观测。因此，消除了诊断的分布询问偏差。我们P2A的诊断分支还以自上而下方式调节询问分支，以收集能迅速接近决策阈值的症状证据。
　　值得注意的是，我们的P2A不仅是一种减少分布偏差的模型，而且是一种多学科融合的方法，其将人类学，因果关系，神经科学和机器学习的新思想和优点汇总在一起。正如许多人类学家指出的那样，人类实现全局决策的决定性因素是能够在精神上描绘环境，并在这种精神表示中进行推理和干预，例如想象类似“What if I open the box?”的问题。J. Pearl and M. A., Hernan认为，为学习机器配备因果推理工具对提高学习速度并达到人类水平的性能至关重要。在神经科学中还有其他生物学发现，当进行顺序决策时，人脑中有双重过程，且每个过程具有不同的功能。
　　代表性的观点之一是，双重过程的认知结构区分了显式和隐式的认知过程。顶层过程更加理性，主要为了追求长远价值，而底层过程更加感性，且对时间的利用更加敏感。尤其是，最近的“as soon as possible”的效果表明，底层过程取决于奖赏以及尽快获得一些东西，并通过逐步的试错来学习，例如RL。

　　总体而言，我们论文的主要贡献在三个方面：i）我们确定了存在于先前研究的患者模拟器中的默认答案偏差，并提出了一种新的患者模拟器PBP，这也可能对其他被动收集观测数据的RL任务具有启发；ii）我们还确定了分布询问偏差，并提出了一种新的MDA agent P2A，以通过干预来消除分布偏差；iii）P2A通过引入启发式神经“决策阈值”来主动确定何时停止询问，从而实现可靠且可解释的决策。考虑到解决的因果关系问题，我们将由PBP和P2A组成的框架命名为Causality-Aware MDA (CA-MDA)。实验结果表明：i）我们的PBP在回答反事实症状询问并产生更多信息的答案方面表现出色；ii）与其他现有的MDA方法相比，我们的P2A在捕获症状疾病关系并将其推广到OOD的情况更好，并具有采样高效和鲁棒的优势。
　　本文的其余部分安排如下。第2节全面审查了相关工作。第3节介绍了CA-MDA的背景，已确定的因果问题以及我们的CA-MDA框架的制定。第4节在两个公开的MDA基准上展现了实验结果及人工评估结果。在第5节中，我们讨论了我们方法的局限性。最后，第6节对本文进行了总结。

2.相关工作

我们的基于倾向的患者模拟器和渐进保证agent包含三种关键成分：流行的因果推理技术propensity score matching (PSM)，对话系统和医学诊断助手中的用户模拟器，强化学习方法。在因果推理的领域，近年来提出了许多不同的方法，根据因果关系是显式还是隐式建模的，大约可以将其分为两个分支，即结构化因果模型（SCM）框架和潜在结果框架（PO）。基于SCM的方法通常包含因果图（CD）和结构化因果方程。然后，将收集的数据注入模型中以推断因果效应。最近，许多基于CD的方法在计算机视觉，强化学习等领域中被提出。这些工作中的大部分都是基于population的一般CD。在MDA中，由于个体差异，患有相同疾病的患者可能患有不同的症状。为了建模这种个体级别的关系，因果图可以将个体信息包括到图中。此外，模型无关的因果推理框架（即潜在结果框架（PO））在没有显式因果模型的情况下从被动观察数据中产生因果效应，并且还能够处理个体的因果效应。
　　在MDA中，收集到的对话记录是被动观察到的，即缺少未观察到的症状。当存在不受控制的混杂因子或受控对撞时，通常会引入偏差。这些偏差通常无法通过增加更多数据来解决。为了消除这些偏差，有许多成熟的因果推理技术，例如两阶段最小二乘，后门调整等。这项工作中确定的反事实症状询问问题是由于对撞引起的偏差。消除对撞偏差的一种解决方案是通过提供忽视能力来关闭对撞影响的路径。可以通过匹配技术获得这种忽视能力。在MDA中，收集的数据通常非常稀疏，因此由于缺乏重叠的问题，普通的匹配方法通常是不可行的。为了解决此问题，引入了倾向分数匹配（PSM），以估计样例的低维倾向以进行匹配。
　　与我们的模拟器类似，当前的工作同样提出在收集的数据上构建患者模拟器。但是，他们的患者模拟器忽略了默认答案偏差。特别地，他们采用了患者-医生的对话记录来产生响应，并且训练好的agent不可避免地会受到设计的模拟器中偏差的影响。为了填补缺失的数据，[12]将环境模型合并到对话agent中以生成模拟的用户经验，但是，这很容易生成与原始数据相似的数据。
　　至于面向任务的对话agent，大部分当前的面向任务的对话系统都采用强化学习框架（RL），而另外一些工作采用了seq2seq的对话生成方式。对于医疗对话系统，由于存在大量的症状，强化学习是更好的选择。由于价值函数所带来的良好近似能力，深度强化学习获得了巨大的成功。根据动作空间的类型，当前的RL方法可以分为两类，即离散控制和连续控制。在医疗诊断助手中，症状询问和疾病诊断的动作是离散的。因此，大多数当前的MDA方法利用经典的离散控制方法，例如Deep Q-Network (DQN)选择动作。[1]应用DQN使用合成数据诊断。 [3]首先使用DQN在真实数据上进行实验。为了包括能提高诊断性能的显式医学归纳偏差，KR-DQN提出了一个端到端模型，以症状-疾病知识为指导训练。KR-DQN应用了症状和疾病的预定义条件概率，以改变DQN估计的Q值。此外，这些方法中的大多数将症状询问和疾病诊断动作整合到一个单一的策略网络中。
　　不同的是，我们的工作遵循MDA在现实生活中的逻辑，并将其作为序列判别决策问题提出。序列判别决策是在人类日常身体和经济决策中发现的自然认知过程。在对神经经济学的研究中，研究人员建立了一种双过程理论，可以在做出经济和身体决定时解释人脑中的神经传播模式。为了建模决策过程，神经经济学提出了一个扩散模型。受这些发现的启发，我们提出的双过程P2A同样结合了诊断器确定何时进行疾病通知的决策阈值概念。此外，我们的方法将神经科学中的二分类设置扩展到计算上的多分类设置。和我们的工作类似，PG-MI-GAN采用了来自询问策略的单独诊断器。具体而言，它训练了一个询问生成器，以生成判别器无法区分的询问序列，并进一步使用预训练的诊断器来微调生成器。正如我们发现的那样，诊断器的设计需要考虑间接偏差，分布偏差以及训练偏差，以更好地捕获症状-疾病的关系并提高诊断agent的可迁移能力。
　　此外，作为医疗应用程序，MDA agent还需要考虑其决策的不确定性，以提供一个鲁棒且可信赖的诊断结果。当前的大多数MDA agent被允许无需任何调节即可进行疾病的通知。与之不同的是，我们的MDA agent采取不确定性来增强决策过程。目前有很多工作研究如何结合不确定性和探索性。但是，与我们工作不同的是，这些工作并没有采用不确定性来为序列决策提供停止机制。

3. CAUSALITY-AWARE MDA

3.1 Preliminaries

如图1所示，诊断记录由自我报告，现有症状 y = [ y a ] a = 1 n ∈ { − 1 , 0 , 1 } n \textbf y=[y_a]^n_{a=1}∈\{-1,0,1\}^n y=[ya​]a=1n​∈{−1,0,1}n（-1 for ‘no’, 0 for ‘not sure’, 1 for ‘yes’），以及真实疾病标签$d\in [1,m]$组成，其中$n$是症状的数量，$m$是疾病的数量。
　　Reinforcement learning。MDA任务通常被定义为马尔可夫决策过程（MDP）问题，并使用元组 M = { S , A , P , R , γ } \mathcal M=\{\mathcal S,\mathcal A,\mathcal P,\mathcal R,γ\} M={S,A,P,R,γ}进行表示。$\mathcal{S}\in {\mathbb{R}}^n$表示状态空间，其中${\text{s}}_t\in \mathcal{S}$负责维护到时刻$t$所有被提及的症状值 (i.e., -2 for non-inquired symptom, -1 for ‘no’, 0 for ‘not sure’ and 1 for ‘yes’)。$A\in {\mathbb{N}}^{n+m}$表示agent的动作空间，其中$a\in \mathcal{A}$是症状询问或疾病诊断。$\mathcal{R}:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$是用于度量诊断过程的奖赏函数。$\mathcal{P}:\mathcal{S}\times \mathcal{A}\to \mathcal{S}$是状态转移概率。强化学习的目标是通过策略来选择动作$\pi :\mathcal{S}\to \mathcal{A}$，以最大化期望累积奖赏：$\eta (\pi )={\mathbb{E}}_{\pi ,\mathcal{M}}[{\sum }_{t=0,(s_t,a_t)〜\pi }^T{\gamma }^t\mathcal{R}(s_t,a_t)]$（$T$是最终步长）。$\gamma \in [0,1]$是衰减因子。初始状态$s_0$由在自我报告中被提到的症状（也称为显式症状）初始化。MDA和经典RL任务（例如Atari 2600和MuJoCo）之间的最大区别在于，MDA agent需要主动决定何时通过告知最终诊断来终止交互。通常，任务中的症状被视为患者回答的原因，这使得能从因果推理的角度解决该任务。

3.2 Sequential discriminative decision making

　　与先前的工作通过RL将询问和诊断融入到黑盒神经网络进行学习不同，我们的论文将其视为序列判别决策问题。 图5描绘了先前工作（左）和我们工作（右）之间的差异。具体而言，我们采用RL agent作为环境与判别器之间的接口。然后，RLagent从环境中询问信息（观测数据），并将观测结果汇总以作为判别器的状态。判别器负责通过主动通知判别决策来结束交互。通过这种方式，我们提出的诊断agent能够分别由询问和判别的双重过程组成。

3.3 Causal Issues and Solutions

Default-answer bias。为了构建患者模拟器，通过利用诊断记录来演示如何回答agent的询问症状$a$。在给定的记录中，模拟器可以访问现有症状$\text{y}$和疾病标签$d$。此外，模拟器可以回答事实症状的询问，但是无法回答记录中未观察到的反事实症状询问，如图1所示。图2中的因果关系（CR）有：
　　(i) Inquiry, symptom → observation (for each symptom)。
　　CR(i) 表示每种症状的观察是由症状和询问引起的。基于CR(i)，如果他们的对抗器被控制（即非询问观测），那么询问和症状之间不具有因果关系。例如，传统患者模拟器只能用“不确定”来回答反事实的症状询问，因为它将未观察到症状的询问节点控制为“非询问”。为了推断出非询问和症状的因果关系，最直接的解决方案是去除对碰撞器（即非询问观测）的控制。为了实现这一目标，我们采用与[45]类似的方法，以收集具有类似协变量的记录。通过这种方式，在匹配的记录中，非询问观察是不同的（即脱控）。
　　但是，MDA记录的协变量（例如，查询的观测值）非常稀疏，这使样本变得极难匹配。为了解决这种缺乏重叠问题，提出了倾向得分匹配（PSM）以估计一个等价物，以及更紧凑的表示匹配，例如倾向得分$P(action|covariates)$。正如附录A中解释的那样，给定相同的倾向得分，上述的忽视能力会存在，因此PSM阻止了从“询问”到“症状”的影响路径。在MDA任务中，给定具有协变量$(\text{y},d)$的记录，倾向得分为$P(A|\text{y},d)$，其中$A$是事实症状询问。在我们的论文中，我们不仅需要匹配与询问相关的倾向，也需要匹配与症状相关的倾向。因此，与$P(A|\text{y},d)$不同，我们采用了更严格的倾向得分，同时考虑询问和症状的存在，即$P(Y_a|\text{y},d)$，其中$a$是症状询问，$Y_a$是询问症状的存在。假设症状仅取决于疾病和观察到的症状，所有症状询问的倾向评分被计算为$P(\text{Y}|\text{y},d)={\prod }_{a}P(Y_a|\text{y},d)$。
　　Distributional inquiry bias。如第一节所述，分布询问偏差会导致agent在询问到足够症状之前就停止通知疾病，如图4a所示，具有如下CR：
　　(ii) Simulated patient → inquired observations
　　(iii) Distributional inquiry bias, inquired observations → stop inquiring
　　(iv) Simulated patient, stop inquiring → non-inquired observations
　　(v) All observations → diagnosis
　　根据上述CR，应删除CR (iv) 中的“stop inquiring”，以使诊断器仅根据模拟患者的信息进行诊断。为了实现这一目标，我们利用干预措施阻止了从stop inquiring到non-inquired observations的路径。正式地，通过数学运算符$do(x)$来定义干预措施，该数学运算符通过从模型中删除某些功能，并用常数$X=x$替换它们，同时保持模型的其余部分不变，从而模拟了物理干预措施。在我们的CD中，为了删除“stop inquiring”的功能，我们使用$do(Causesofnon-inquiredobservations=simulatedpatient)$。
　　该操作从图4a中将CD减少到具有如下CR的图4b：
　　(vi) Simulated patient → inquired observations
　　(vii) Simulated patient → non-inquired observations
　　(viii) All observations → diagnosis
　　根据患者的诊断信息，诊断器使用减少后的CD专注于诊断学习。为了完成干预，诊断agent可以根据CR (vi)的inquired observations结果推断出模Simulated patient。 根据 CR (vii)，可以根据Simulated patient确定non-inquired observations。此外，该agent使用询问和估计的非询问观测值根据CR(viii)进行诊断。

3.4 Formulation

　　为了解决上述两个代表性偏差，我们提出了CA-MDA，CA-MDA由基于倾向的患者模拟器（PBP）和渐进保证agent（P2A）组成。PBP和P2A之间的相互作用的概述如图6所示。

3.4.1 Propensity-based Patient Simulator

4
　　Propensity score modeling。正如上一节所介绍的那样，PSM的目的是阻止图2中从Inquiry到non-inquired ‘Symptom’路径的影响，以消除对撞偏差。这可以通过使用记录的相似估计倾向得分匹配$P(\text{Y}|\text{y},d)$来实现。直观地，倾向得分代表与患者询问相关的倾向。倾向得分匹配是使用相似倾向匹配不同的患者，因为这些患者可能会经历相同的诊断过程。从这个意义上讲，这些患者的诊断过程是可交换的。在这些匹配的患者中，排除了与症状相关的唯一外部因素（即询问），因此协变量对症状的影响成为因果。由于倾向得分也代表了协变量，因此匹配的患者的症状相似。
　　我们使用多层感知机（MLP）$f_{\varphi P}(\cdot )$来建模$P(\text{Y}|\text{y},d)$，其中$\varphi P$表示网络参数，通过减少交叉熵损失$CE(P(Y),y)=-ylogP(y)$进行训练。我们利用自监督策略来训练$f_{\varphi P}(\cdot )$，以估计任何症状询问$a$的潜在症状。具体来说，我们使用二元掩码$\text{m}$对$\text{y}$进行mask，并训练$f_{\varphi P}(\cdot )$，以重建$\text{y}$。重建目标是：
$$\underset{\varphi P}{\min }\sum _{i=1}^N\sum _{a=1:n,y_a\ne 0}\sum _{\text{m}}CE(f_{\varphi P}({\text{y}}^i\odot \text{m},d^{(i)}{)}_a,y_a^{(i)}).\text{\hspace{1em}(1)}$$
　　训练后，我们采用倒数第二个完全连接层的输出作为倾向得分$f_{\hat{\varphi }P}(\cdot )$，因为它的维度要小得多，并且与最后一层相比，信息更紧凑。
　　Potential existence of symptoms estimation。给定一个锚记录$p$，我们展示了模拟器如何估计未观测症状$a$的存在性。我们的模拟器会探索所有与记录$p$具有相同疾病的记录 { . . . , q , . . . } \{...,q,...\} {...,q,...}（即$d^{(q)}=d^{(p)}$），并且这些记录观察到的症状中也包含$a$（即$y_a^{(q)}\ne 0$）。它消除了询问症状和疾病不相关的信息。与$p$相关的记录$q$被形式化为：
$$p(q|p,a)\propto \mathbb{I}(d^{(q)}=d^{(p)}\wedge (y^{(q)}\ne 0))\times e^{-\frac{||f_{\varphi P}^{(p)}-f_{\varphi P}^{(q)}|{|}^2}{{\sigma }^2}},\text{\hspace{1em}(2)}$$
其中$e^{-\frac{||f_{\varphi P}^{(p)}-f_{\varphi P}^{(q)}|{|}^2}{{\sigma }^2}}$表示非参数密度核（$\sigma >0$表示倾向得分的标准偏差）。患者记录$q$和$p$倾向得分的相似性表明这些记录症状的存在性可能更相似。$\mathbb{I}(\cdot )$是一个指示函数，如果满足括号中的命题逻辑公式，则返回1，否则返回0。然后，患者模拟器可以从$q^{\prime }〜P(q|p,a)$采样记录，并使用其症状存在标签$y_a^{(q^{\prime })}$作为锚记录$p$潜在症状$a$的结果。更多细节在附录A中。

3.4.2 Progressive Assurance Agent

　　为了解决分布询问偏差，我们提出了一种渐进保证agent（P2A），该agent由两个独立但彼此合作的分支组成，以分别用于症状询问和疾病诊断，如图6所示。在P2A中，“fast but impulsive”询问分支从PBPS中询问症状以得到${\text{s}}_t$，来最大化奖赏总和，同时“slow but rational”诊断分支想象并推理未来场景，来估计疾病以及每一步的置信度，直到置信度足够（满足决策阈值）通知疾病。询问分支由诊断分支驱动，以询问能够尽快满足决策阈值的症状。更多细节可看附录B。
　　Diagnosis Branch。为了消除3.3节中提到的偏差，我们的P2A干预仅受模拟患者影响的观测结果。具体而言，我们的P2A根据询问的观察${\text{s}}_t^v$首先推理模拟患者最终的可能状态${\hat{\text{s}}}_t$，即$P({\hat{\text{s}}}_t|{\text{s}}_t^v)$。 然后，P2A使用估计的模拟患者对未询问症状的观察结果${\text{s}}_t^u$进行干预，即$do(s_t^u={\hat{\text{s}}}_t-{\text{s}}_t^v)$（图4b）。直观上，可以将这种干预过程作为“想象并推理未来交互，以获得足够全面的患者状态来进行可信赖诊断”。之后，P2A将询问和干预症状作为判别诊断器的输入$P(d|{\hat{\text{s}}}_t)$。总的来说，P2A诊断器通过$P(d|{\text{s}}_t^v)={\sum }_{{\hat{\text{s}}}_t}P(d|{\hat{\text{s}}}_t)P({\hat{\text{s}}}_t|{\text{s}}_t^v)$使用观察的症状来诊断。我们分别为$P({\hat{\text{s}}}_t|{\text{s}}_t^v)$和$P(d|{\hat{\text{s}}}_t)$训练干预器$f_{\varphi G}(\cdot )$和判别诊断器$f_{\varphi B}(\cdot )$。
　　Intervener。干预器旨在预测当前询问状态${\text{s}}_t^v$的最终症状状态$\hat{\text{s}}$。因此，我们将其建模为生成问题。$\varphi M$是生成器$f_{\varphi G}(\cdot )$的参数，其目标是定义如下的交叉熵：
$$\underset{\varphi G}{\min }\sum _{i=1}^N\sum _{a=1:n,s_{i,a}\ne -2}\sum _{\text{m}}CE(f_{\varphi G}({\text{s}}_i\odot \text{m}{)}_a,s_{i,a}),\text{\hspace{1em}(3)}$$
其中$\text{m}$是和等式1相同二元mask，而$f_{\varphi G}$的目标是恢复被mask的信息。如图6所示，通过使用蒙特卡洛采样对生成模型$f_{\varphi G}(s_t)$采样k个可能的最终状态 { s ^ ( k ) } k = 1 K \{\hat{\textbf s}^{(k)}\}^K_{k=1} {s^(k)}k=1K​。 请注意，在这些最终状态中，${\text{s}}_t^v$的询问症状保持不变。
　　在完成干预后，$K$个假想的最终状态被带入诊断器$f_{\varphi B}(\cdot )$以检查是否满足决策阈值。
　　Decision Threshold。直观地，当医生确信询问更多症状不会推翻他的诊断时，他就会停止询问以告知疾病。因此，我们提出决策阈值（DT）来模仿这种内省的过程，也就是说，如果agent认为首选疾病的可能性足够高，则agent将停止询问以告知首选疾病，以便询问更多症状不会有更大概率推翻首选疾病。为了估计每种疾病的可能性及其置信度，采用bootstrapping技术来训练ensemble诊断器。
　　bootstrapping诊断器使用对话的最终状态进行训练。训练的最终状态是基于从数据缓冲区进行有放回采样的状态来生成的。具有参数${\varphi }_{B,i}$的诊断器$i$的训练目标是：
$$\underset{{\varphi }_{B,i}}{\min }\sum _{\widehat{\text{s},d}}CE(f_{{\varphi }_{B,i}}(\hat{\text{s}}),d)s.t.\forall i\in [1,B].\text{\hspace{1em}(4)}$$
　　然后将在intervener中生成的最终状态送入$B$个bootstrapping诊断器中，从而得到最终的疾病概率集合 { p t ( k , b ) } k = 1 , b = 1 K , B \{\textbf p^{(k,b)}_t\}^{K,B}_{k=1,b=1} {pt(k,b)​}k=1,b=1K,B​。然后，疾病概率集最终用于计算疾病的期望${\text{µ}}_t=[{\mu }_t^{(1)},\cdots ,{\mu }_t^{(m)}]$和标准差${\text{σ}}_t=[{\sigma }_t^{(1)},\cdot \cdot \cdot ,{\sigma }_t^{(m)})$：
$${\text{µ}}_t=\frac{1}{KB}\sum _{b=1}^B\sum _{k=1}^K{\text{p}}_t^{k,b},{\text{σ}}_t^2=\frac{1}{KB}\sum _{b=1}^B\sum _{k=1}^K({\text{p}}_t^{(k,b)}-{\text{µ}}_t{)}^2,\text{\hspace{1em}(5)}$$
期望和标准差进一步用于计算疾病的置信区间。此外，bootstrapping诊断器在减少由数据采样过程和参数初始化引入的意外噪声效果方面也很受欢迎。这种噪声的效果会妨碍该模型的分布内性能。
　　使用均值和方差，如果首选疾病的概率超出了其他疾病概率$6\sigma$置信区间的上限，则将达到DT。将选择的首选疾病表示为$i$，即$i=argma{x}_j{\mu }_t^{(j)},\forall j\in [1,m]$。DT被形式化为：
$$DT({\mu }_t,{\text{σ}}_t)=\{\begin{array}{ll}True,& \forall j\ne i,{\mu }_t^{(i)}>{\mu }_t^{(j)}+3{\sigma }_t^{(j)},\\ False,& otherwise\end{array}.\text{\hspace{1em}(6)}$$
　　Inquiry Branch。诊断分支决定询问分支来探索有意义的症状。询问分支采用Q网络，该网络以状态${\text{s}}_t$和当前疾病概率${\text{u}}_t$的串联作为输入，来预测动作$a_t$。
$$a_t=ma{x}_{a}Q({\text{s}}_t,{\text{µ}}_t,a;\theta ).\text{\hspace{1em}(7)}$$
　　参数化策略采用如下梯度训练：
$${\nabla }_{\theta }L={\mathbb{E}}_{{\text{s}}_t,{\text{µ}}_t,a_t,{\text{s}}_{t+1},{\text{µ}}_{t+1}}\left[\right(r_t+\gamma ma{x}_{a}Q({\text{s}}_{t+1},{\text{µ}}_{t+1},a;{\theta }_{targ})-Q({\text{s}}_t,{\text{µ}}_t,a_t;\theta )){\nabla }_{\theta }Q({\text{s}}_t,{\text{µ}}_t,a_t;\theta )],\text{\hspace{1em}(8)}$$
其中${\theta }_{targ}$表示目标Q网络，其参数的更新通过使用衰减因子$\alpha$来稳定训练：
$${\theta }_{targ}=\alpha {\theta }_{targ}+(1-\alpha )\theta .\text{\hspace{1em}(9)}$$
　　Reward for a single goal。现有的RL方法设计一个复杂的奖赏函数，以训练策略来最大化累积奖赏。但是，奖赏的设计对不同的情况很敏感，这使得累积奖励的含义太复杂而无法理解。通过将疾病诊断从策略中份离，该策略的目标变得具体：尽快达到DT。因此，通过将奖赏设置为常数$r_t=-0.1$，以鼓励agent快速满足DT。