摘要
我们提出了Position Interpolation (PI),其能够将基于RoPE的预训练LLM(例如LLaMA模型)的上下文窗口大小扩展到32768,并且仅需少量的微调(在1000步中),同时在需要长上下文的各种任务上证明了强大的经验结果 ,包括从Llama 7b到65B的passkey检索,语言建模以及长文档摘要。同时,通过位置插值扩展的模型在其原始上下文窗口内的任务上也相对较好地保留了质量。为了实现这一目标,位置插值线性向下缩放了输入位置索引以匹配原始的上下文窗口大小,而不是外推超过训练时所用的上下文长度,因为这可能会导致灾难性的较高的注分数分,从而完全破坏了自注意力机制。我们的理论研究表明,插值注意力分数的上界至少比外推的上界小了约600倍,这进一步证明了其稳定性。通过位置插值扩展的模型保留了其原始网络结构,并可以重复使用大多数预先存在的优化和基础架构。
1.介绍

大型语言模型(LLM)通常带有预定义的上下文窗口大小。例如,对LLaMA模型的输入必须小于2048个token。在诸如进行长对话,长文档摘要或执行长期计划之类的应用中,这种预定义的上下文窗口限制经常无法满足要求。对于这些应用,首选具有更长上下文窗口的LLM。但是,从头训练具有较长上下文窗口的LLM需要大量资源。这自然会导致一个问题:我们是否可以扩展现有预训练LLM的上下文窗口?
一种直接的方法是用更长的上下文窗口微调现有的预训练Transformer。但是,从经验上讲,我们发现以这种方式训练的模型需要非常长的训练时间才能调整到长上下文窗口。在训练了10000多个batch之后,有效的上下文窗口仅少量增长,从2048年移至2560(表4)。这表明这种方法效率低下,无法扩展到更长的上下文窗口。
尽管某些技术(例如ALiBi和LeX)能够扩展Transformers的长度,即在短上下文窗口上训练,并在更长的窗口上推理,但许多现有的预训练LLM,包括LLaMA,使用的位置编码具有较弱的外推特性(例如,RoPE)。因此,这些技术用于扩展此类LLM的上下文窗口大小的适用性仍然有限。
在这项工作中,我们介绍了Position Interpolation,以对某些现有预训练的LLM(包括LLaMA)进行上下文窗口的扩展。其关键的想法是,我们直接将位置索引向下缩放,以便最大位置索引与预训练阶段中的上下文窗口限制匹配。有关描述请参见图1。换句话说,为了容纳更多的输入字符,我们利用了位置编码可以应用于非整数位置的事实,从而在整数位置附近插入位置编码,而不是扩展训练好的位置编码。我们从理论上验证了我们的方法,表明插值注意力分数的上界比外推要小得多(在LLaMA 7B的设置中小了600倍),因此更稳定。因此,位置插值编码更容易被模型适应。
从经验上讲,我们发现位置插值非常有效,仅需要很短的微调就能使模型完全适应较大的上下文窗口。我们提出了通过位置插值将7~65B的LLAMA模型的上下文窗口从最初的2048扩展到32768的实验结果。我们的结果表明:
- 位置插值可以轻松地启用非常长的上下文窗口(例如32768),只需要在Pile数据集上进行1000个步骤微调即可实现良好的质量。与预训练成本相比,微调的成本可以忽略不计。这证实了我们的假设,即模型适应位置插值编码相对容易。
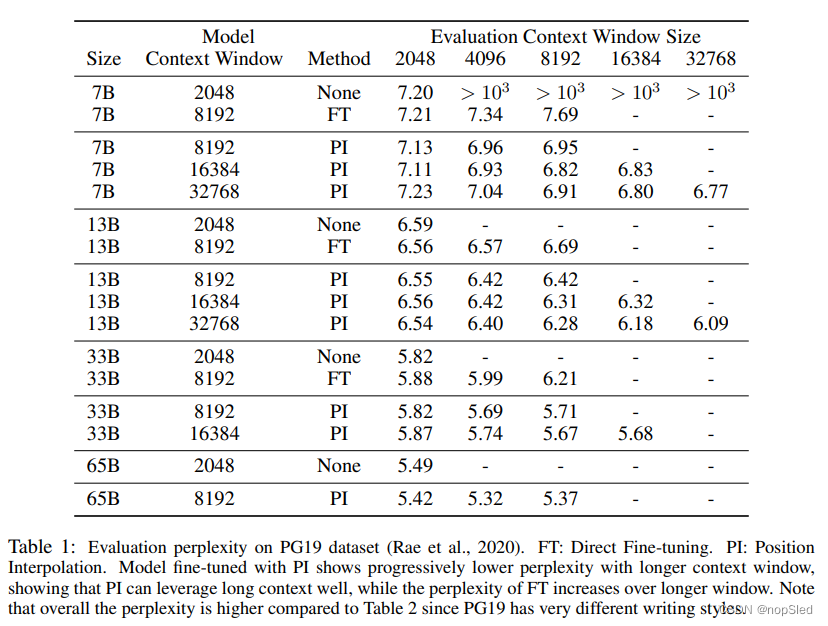
- 位置插值会产生强大的模型,可以有效地利用大量扩展的上下文窗口。我们表明,按位置插值扩展的模型从较长的上下文窗口中获得了用于文本建模的很大困惑度增益,我们表明,由于上下文窗口的扩大,这种困惑可以减少。我们还将位置插值应用于长文本摘要任务,并展示竞争性能。
- 位置插值可在其原始上下文窗口大小的任务中保证模型质量相对良好。我们在原始的LLaMA基准测试中为扩展的LLaMA模型提供了各种评估结果。与原始的LLaMA模型相比,扩展的LLaMA模型在2048token约束内对几个标准基准测试仅具有较小的下降。
我们的结果突显了Transformer模型具有“将序列长度扩展到比训练过程中长度更长序列”的先天能力。我们重申了这一假设,并提出先前已知的扩展到更长语言建模序列的弱点可能是由于对位置编码的直接扩展导致,并且通过位置插值编码可以在很大程度上减轻这一缺点。
Concurrent work。在我们开源之前,我们发现同一时期的博客文章(SuperHOT kaiokendev),也在RoPE中差值位置编码,以将上下文窗口从2K扩展到8K。最近,开源社区在Reddit Post和GitHub Issues中选择了它,这表明使用LoRA进行微调似乎也很好。我们的论文显示了一个全参数的微调,一直到65B模型也能与位置差值具有很好的适应,我们还提供了理论解释,为什么插值可以比直接扩展要更稳定得多。
2.METHOD
2.1 BACKGROUND: ROTARY POSITION EMBEDDING (RoPE)
Transformer模型通常以位置编码的形式注入显示的位置信息,以表示输入顺序。我们考虑旋转位置嵌入(RoPE),这是LLaMA模型中使用的位置编码方式。给定一个位置索引
m
∈
[
0
,
c
)
m∈[0,c)
m∈[0,c)和一个嵌入向量
x
:
=
[
x
0
,
x
1
,
.
.
.
,
x
d
−
1
]
⊤
\textbf x:=[x_0,x_1,...,x_{d-1}]^⊤
x:=[x0,x1,...,xd−1]⊤,其中
d
d
d是注意力头的维度,RoPE定义了一个矢量和值的复杂函数
f
(
x
,
m
)
f(\textbf x, m)
f(x,m),如下所示:
f
(
x
,
m
)
=
[
(
x
0
+
i
x
1
)
e
i
m
θ
0
,
(
x
2
+
i
x
3
)
e
i
m
θ
1
,
.
.
.
,
(
x
d
−
2
+
i
x
d
−
1
)
i
m
θ
d
/
2
−
1
]
⊤
(1)
f(\textbf x,m)=[(x_0+ix_1)e^{im\theta_0},(x_2+ix_3)e^{im\theta_1},...,(x_{d-2}+ix_{d-1})^{im\theta_{d/2-1}}]^⊤\tag{1}
f(x,m)=[(x0+ix1)eimθ0,(x2+ix3)eimθ1,...,(xd−2+ixd−1)imθd/2−1]⊤(1)
其中
i
:
=
−
1
i:=\sqrt{-1}
i:=−1是一个虚数,并且
θ
j
=
1000
0
−
2
j
/
d
\theta_j=10000^{-2j/d}
θj=10000−2j/d。使用RoPE,自注意力的分数为:
a
(
m
,
n
)
=
R
e
⟨
f
(
q
,
m
)
,
f
(
k
,
n
)
⟩
=
R
e
[
∑
j
=
0
d
/
2
−
1
(
q
2
j
+
i
q
2
j
+
1
)
(
k
2
j
−
i
k
2
j
+
1
)
e
i
(
m
−
n
)
θ
j
]
=
∑
j
=
0
d
/
2
−
1
(
q
2
j
k
2
j
+
q
2
j
+
1
k
2
j
+
1
)
c
o
s
(
(
m
−
n
)
θ
j
+
(
q
2
j
k
2
j
+
1
−
q
2
j
+
1
k
2
j
)
s
i
n
(
(
m
−
n
)
θ
j
)
=
:
a
(
m
−
n
)
(2)
\begin{array}{cc} a(m,n) =Re⟨f(\textbf q,m),f(\textbf k, n)⟩\\ =Re\bigg[\sum^{d/2-1}_{j=0}(q_{2j}+iq_{2j+1})(k_{2j}-ik_{2j+1})e^{i(m-n)\theta_j}\bigg]\\ =\sum^{d/2-1}_{j=0}(q_{2j}k_{2j}+q_{2j+1}k_{2j+1})cos((m-n)\theta_j+(q_{2j}k_{2j+1}-q_{2j+1}k_{2j})sin((m-n)\theta_j)\\ =: a(m-n) \end{array}\tag{2}
a(m,n)=Re⟨f(q,m),f(k,n)⟩=Re[∑j=0d/2−1(q2j+iq2j+1)(k2j−ik2j+1)ei(m−n)θj]=∑j=0d/2−1(q2jk2j+q2j+1k2j+1)cos((m−n)θj+(q2jk2j+1−q2j+1k2j)sin((m−n)θj)=:a(m−n)(2)
仅取决于通过三角函数的相对位置
m
−
n
m-n
m−n。这里的
q
\textbf q
q和
k
\textbf k
k是特定注意力头的query和key向量。在每一层中,RoPE都应用于query和key嵌入,以计算注意力分数。
2.2 DIRECT EXTRAPOLATION

尽管RoPE中的注意力分数仅取决于我们想要的相对位置,但其外推性能并不是特别出色。特别是,当直接扩展到训练中未见过的较大上下文窗口时,困惑度可能会达到非常高的数字(即
>
1
0
3
>10^3
>103),这与未经训练的模型相当。
理想情况下,我们希望看到在大小
L
=
2048
L=2048
L=2048的上下文窗口上训练的模型,在更长的上下文窗口上仍能够合理工作,但可能无法利用大于
L
L
L以外的信息。在对长度3000的问题进行回答时,在
L
=
2048
L=2048
L=2048窗口大小训练的模型无法利用位置0的信息,但仍然可以利用位置2900处的信息。与该期望相反,实际上我们看到了灾难性的行为,即长度为3000的问题无法被正确回答,即使证据位于位置2900处。
该问题背后的原因是什么?根据(Su et al., 2021)的第3.4.3节, 如果注意力分数
a
m
−
n
a_{m-n}
am−n随着相对距离
∣
m
−
n
∣
|m-n|
∣m−n∣增加而减少,那这是如何发生的呢,并且远距离的内容并不重要吗?事实证明,在(Su et al., 2021)第3.4.3节中得出的上界可能太松了:虽然它确实会随
∣
m
−
n
∣
|m-n|
∣m−n∣而衰减,但其界限仍然可以很大(即边界主要取决于
v
j
v_j
vj的大小),因此是假降低的。实际上,如果我们将所有三角函数视为基础函数(即
ϕ
j
(
s
)
:
=
e
i
s
θ
j
ϕ_j(s):=e^{isθ_j}
ϕj(s):=eisθj),并将等式2视为基础扩展,则如下:
a
(
s
)
=
R
e
[
∑
j
=
0
d
/
2
−
1
h
j
e
i
s
θ
j
]
(3)
a(s)=Re\bigg[\sum^{d/2-1}_{j=0}h_je^{is\theta_j}\bigg]\tag{3}
a(s)=Re[j=0∑d/2−1hjeisθj](3)
其中
s
s
s是query和key之间的位置跨度,而
h
j
:
=
(
q
2
j
+
i
q
2
j
+
1
)
(
k
2
j
−
i
k
2
j
+
1
)
h_j:=(q_{2j}+i_{q2j+1})(k_{2j}-ik_{2j+1})
hj:=(q2j+iq2j+1)(k2j−ik2j+1)是复数,取决于
q
\textbf q
q和
k
\textbf k
k(这里的
h
j
h_j
hj和RoPE第3.4.3中
h
j
h_j
hj的定义一样)。现在,问题变得很清楚:如图2所示,
a
s
a_s
as在[0,2048]的范围内可能很小,但在超出该区域时产生了巨大的值。根本的原因是三角函数
{
ϕ
j
}
\{ϕ_j\}
{ϕj}(具有足够大的
d
d
d)是通用近似器,可以拟合任何任意函数。因此,对于
a
s
a_s
as,总是存在系数
{
h
j
}
\{h_j\}
{hj}(即key和query),该系数与[0,2048]中的小函数值相对应,但在超出的区域中大得多。
2.3 PROPOSED APPROACH: POSITION INTERPOLATION (PI)
在图2中,由于基础函数
ϕ
j
ϕ_j
ϕj的平滑度插值更加稳定,不会导致异常值。因此,与扩展等式3中的注意力分数到
s
>
L
s>L
s>L相反,我们如何定义一个新的注意分数
a
~
(
s
)
=
a
(
L
s
/
L
′
)
\tilde a(s)=a(Ls/L')
a~(s)=a(Ls/L′),其中
L
′
L'
L′是更长的上下文窗口? 正式地,我们用
f
′
f'
f′替换RoPE的
f
f
f,定义如下:
f
′
(
x
,
m
)
=
f
(
x
,
m
L
L
′
)
.
(4)
f'(\textbf x, m)=f(x, \frac{mL}{L'}).\tag{4}
f′(x,m)=f(x,L′mL).(4)
我们将这种在位置编码上的变换称为Position Interpolation。在此步骤中,我们将位置索引从
[
0
,
L
′
)
[0,L')
[0,L′)减少到
[
0
,
L
)
[0,L)
[0,L),以匹配计算RoPE之前的原始索引范围。因此,作为RoPE的输入,任何两个token之间的最大相对距离已从
L
′
L'
L′降低到
L
L
L。由于我们将扩展前后的位置索引和相对距离的范围保持对齐,因此我们减轻了由于上下文窗口扩展对注意力分数的影响,从而可以允许模型更容易适应。为了进一步证明这种情况,在下面的定理中,我们表明插值注意力分数是良好的:
Theorem 2.1 (Interpolation bound)。

Fine-tuning。我们可以使用下一个token预测任务进一步微调具有插值位置编码的模型,并使用诸如Pile等预训练语料库。在下一节中,我们表明我们的微调过程只需要数十万个样例。我们还发现,微调的结果对示例的选择不敏感。原因可能是该模型是从良好初始化权重开始,并且仅在微调阶段中适应新的上下文窗口,而不是获取新知识。
Other ways to reduce interpolation/extrapolation bound。从插值的表达(等式5)和外推边界(等式8)中,一个常见的项是
m
a
x
j
∣
h
j
∣
max_j |h_j|
maxj∣hj∣,它是query/key点积的最大幅度。如果我们在LLM训练期间对
∣
h
j
∣
|h_j|
∣hj∣执行正则化,可能会减轻甚至解决灾难性的外推误差。实际上,如果我们使用具有适当正则化的岭回归拟合图2中的曲线,则当
s
>
L
s>L
s>L时,外推出的
a
(
s
)
a(s)
a(s)的大小与
[
0
,
L
]
[0,L]
[0,L]内的相当。据我们所知,我们还不知道已经利用了这种正则化的现有LLM训练技术,并将其留给将来的工作。
3.EXPERIMENTS
3.1 SETUP


Appendix









 文章提出PositionInterpolation(PI)方法,允许基于RoPE的预训练大型语言模型(如LLaMA)在少量微调后扩展上下文窗口至32768。PI通过位置插值保持模型质量,避免直接外推可能导致的高困惑度。理论分析表明插值方法比外推更稳定,实验证明PI在长上下文任务中表现出色,且在原窗口大小任务中保留了性能。
文章提出PositionInterpolation(PI)方法,允许基于RoPE的预训练大型语言模型(如LLaMA)在少量微调后扩展上下文窗口至32768。PI通过位置插值保持模型质量,避免直接外推可能导致的高困惑度。理论分析表明插值方法比外推更稳定,实验证明PI在长上下文任务中表现出色,且在原窗口大小任务中保留了性能。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








