Topologies of Reasoning: Demystifying Chains, Trees, and Graphs of Thoughts翻译

摘要

近年来，自然语言处理 (NLP) 领域取得了重大进展，特别是通过新的提示技术来提高大语言模型 (LLM) 的性能。其中，与结构相结合的提示工程已成为一种有前途的范式，其设计包括思维链、思维树或思维图，在这些方法中 LLM 整体推理是由这种图结构引导的。正如众多例子所示，这种范式显着增强了LLM解决众多任务的能力，从逻辑或数学推理到规划或创意写作。为了促进对这个不断发展的领域的理解并为未来的发展铺平道路，我们为有效且高效的LLM推理方案设计了总体蓝图。为此，我们对提示执行pipline进行了深入分析，澄清并明确定义了不同的概念。然后，我们构建了结构增强的 LLM 推理方案的第一个分类法。我们专注于识别所利用结构的基本类别，并分析这些结构的表示、使用这些结构执行的算法以及许多其他结构。我们将这些结构称为推理拓扑，因为它们的表示在一定程度上变得空间化，同时它们包含在LLM上下文中。我们的研究使用所提出的分类法比较了现有的提示方案，讨论了某些设计选择如何导致不同的性能和成本模式。我们还概述了理论基础、提示与LLM生态系统其他部分（例如知识库）之间的关系以及相关的研究挑战。我们的工作将有助于推进未来的提示工程技术。

1.介绍

大型语言模型 (LLM) 已成为现代机器学习 (ML) 的主要工具。源于简单的自然语言处理（NLP）任务，其广泛的潜力已迅速应用于其他领域，例如逻辑推理、规划、医学等。由于LLM的主要交流媒介是自然语言，提示工程已成为一个受到广泛关注和重视的新研究领域。首先，它使任何人都易于使用和尝试，从而实现了LLM和整个生成式人工智能领域的民主化。其次，它具有成本效益，不需要昂贵且耗时的微调或预训练。
　　精心设计 LLM 问题以提高结果的准确性以及逻辑或代数查询等任务的成本效益具有挑战性。尽管LLM的规模和认知能力不断进步，但由于生成式Transformer 模型的从左到右、一次预测一个token的性质，用一个简单的提示解决如此复杂的任务会产生不精确或完全错误的结果。因此，最近的工作重点是引导LLM通过中间步骤找到最终解决方案。此类方案的示例包括思维链 (CoT)、思维树 (ToT)、思维图 (GoT)、AutoGPT、ReAct 或 LLMCompiler。这一系列工作提高了LLM推理的性能。
　　然而，尽管取得了所有这些进步，最先进的方案仍然表现出许多局限性。首先，它们仍然仅限于简单的任务，例如 24 字游戏，因此进一步增强提示以解决复杂的多方面任务至关重要。此外，最先进的提示方案通常需要高昂的推理成本。第三，设计、开发、维护和扩展这些方案很困难。一方面，这是由于“LLM生态系统”的快速发展和丰富，必须无缝集成到提示管道中。这包括检索增强生成 (RAG)、访问互联网、执行 Python 脚本、微调等。另一方面，与LLM推理相关的不同概念没有明确定义，阻碍了新的更强大方案的有效设计。例如，虽然许多方案依赖于LLM thought的概念，但尚不清楚它与提示等概念有何关系。
　　为了解决上述问题，我们首先确定并具体化通用提示执行piplne中的基本构建块和概念。然后，我们在 CoT、ToT 和 GoT等最新方案的背景下分析和阐明这些模块和概念（贡献#1）。我们的研究基于对LLM推理近期工作的广泛分析。然后，我们利用所获得的见解来制定 LLM 推理方案的总体蓝图和分类法，重点关注如何使用推理的基础结构来促进更高效、有效和富有成效的提示（贡献#2）。为此，我们观察到许多最近的提示方案中的推理过程可以建模为图。虽然与 LLM 交互的本质是时序的，但 LLM 推理背后的图结构表示会定期与 LLM 上下文合并，在一定程度上变得空间化，从而形成不同的拓扑。 这些拓扑可以是普通路径图（如 CoT 中）、具有单个根节点的多个并行路径图（如具有自洽推理的 CoT ）、树（如 ToT ）或任意图（如 GoT ）。然后，我们使用我们的分类法来调查和分析现有的提示方案（贡献＃3）。我们将这些方案分解为基本方面，例如用于建模推理过程的图的类别（即拓扑）、推理的表示或推理调用的编码。我们重点研究哪些类别的方案在预测准确性、执行延迟或成本效益方面提供更高的性能（贡献#4）。我们最后列出了新研究方向的开放挑战和潜力（贡献#5）。

2. EVOLUTION OF REASONING TOPOLOGIES

　　我们首先总结推理拓扑的演变；请参阅图 1 了解概述。为了简洁起见，我们尚未精确定义所使用的术语，而是依赖于文献中广泛使用的术语。在第 3-4 节中，我们介绍并讨论精确命名。
　　在基本输入输出（IO）提示中，LLM在收到用户初始提示后立即提供最终答复。LLM 推理中没有中间步骤。链式拓扑，由 Wei et al. [195] 在 Chain-of-Thought 中引入，除了输入和输出之外，还通过结合显式的中间“推理步骤”来改进 IO 提示。 自洽思维链 (CoT-SC) 通过引入源自相同初始输入的多个独立推理链，对 CoT 进行了改进。然后，根据预定义的函数 $S$，从最终想法中选择最佳结果。CoT-SC的动机是利用 LLM 推理中的随机性，因为它可以根据相同的提示生成不同的想法。
　　思维树 (ToT) 通过允许在思维链的任何推理节点进行快速分支，从而提高了 CoT 的限制。 因此，不同的探索路径并不像 CoT-SC 那样本质上是独立的，但在推理过程中可以产生一系列的思想分支来探索不同的选择。单个树节点代表部分解决方案。基于给定的节点，思维生成器构造给定数量的 k 个新节点。然后，状态评估器为每个这样的新节点生成分数。根据用例，可以使用LLM本身进行评估，也可以利用人工评分进行评估。最后，扩展树的调用由所使用的搜索算法（例如 BFS 或 DFS）决定。
　　最后，思维图 (GoT) 可以实现在生成的思维之间构建任意推理依赖关系。与 ToT 类似，每个思想都可以产生多个子思想。然而，每个思想也可以有多个父思想，这可以形成聚合操作。GoT 允许分支（出度 > 1 的思想）和聚合（入度 > 1 的思想）操作，可以表达 - 例如 - 类似于动态规划的推理模式，其中 GoT 子图负责解决子问题，这些子问题然后组合形成最终解决方案。

3.ESSENCE OF GENERAL PROMPT EXECUTION

我们首先通过给出提示pipLine的详细概述（第 3.1 节）来总结一般的提示执行方法，然后为任何提示方案建立一个函数公式（第 3.2 节）。这个表述将有利于我们后续对推理拓扑的分析。

3.1 Basic Prompting Pipeline

　　图 2 总结了提示pipline。图的左侧显示了高层级的用户-AI交互，其中包括用户与LLM基础设施之间的一系列信息交换； 用户发送提示，而LLM发回回复。
　　如图 2 的主要中心部分所示，第 $i$ 个提示交互从用户发送提示 $p_i$ 开始。在输入模型之前，LLM 提供者1可以对提示进行预处理，使其成为 ${\tilde{p}}_i$。 这可能包括添加“系统预提示”或一些额外的元数据、检查是否符合某些策略、提高提示质量、进行检索增强，或者包括运行外部工具（例如 Python 脚本）或访问互联网。预处理后的提示被添加到 LLM 上下文 2，然后被馈送到模型 3。这会产生自回归输出4。模型通常被冻结，使其权重不会改变。在一些考虑的提示方案中，模型还可以进行微调。输出 $o_i$ 可能会进行后处理5，这可能涉及通过额外的神经层运行（例如，用于情感分析）或提供者端的其他形式的后处理，例如检查 NSFW、添加更多元数据</>， 及其他操作。后处理的输出 ${\tilde{o}}_i$ 也会添加到上下文 6 中，并作为回复发送回用户8。请注意，在返回给用户之前，${\tilde{o}}_i$ 也可能会直接反馈给模型，以进行额外的迭代7。

3.2 Functional Formulation & Building Blocks

我们将第 3.1 节中的基本提示pipline形式化。这使我们能够具体化其基本构建模块，促进未来的优化并推动高效和有效的设计。基本功能构建块是 $f_{pre}$（用于提示预处理 1）、$f_{post}$（用于 LLM 输出的后处理 5）、LLM（用于自动生成 LLM 执行 4）、$f_c$（用于确定如何在阶段2中更新上下文）和 $f{\prime }_c$（用于确定在第 6 阶段如何更新上下文）。为此，我们观察到第 $i$ 个提示交互（对于 i = 1 ， . . . a n d   c ′ 0 = { } i=1，...and~c′_0=\{\} i=1，...and c′0​={}）可以正式描述为：
$${\tilde{p}}_i=f_{pre}(p_i)\text{\hspace{1em}(1)}$$
$$c_i=f_c({\tilde{p}}_i,c_{i-1}^{\prime })\text{\hspace{1em}(2)}$$
$$o_i=LL{M}^X(c_i)\text{\hspace{1em}(3)}$$
$${\tilde{o}}_i=f_{post}(o_i)\text{\hspace{1em}(4)}$$
$$c_i^{\prime }=f_c^{\prime }(c_i,{\tilde{o}}_i)\text{\hspace{1em}(5)}$$
其中：

• $p_i$是用户提示中的第$i$个提示交互。
• $f_{pre}(p_i)$是应用到$p_i$的预处理变换。其也许涉及到检索增强生成（RAG），执行脚本，访问网络，以及使用工具。
• ${\tilde{p}}_i$是第$i$个提示的预处理版本。
• $c_i$是从第$i$个提示交互开始的上下文（在执行$f_c$以后）。
• $c_i^{\prime }$是在执行第$i$个提示交互的$f_c^{\prime }$后上下文（注意到实际实现，$c_i$和$c_i^{\prime }$是作为相同的数据结构），注意 c 0 ′ = { } c'_0=\{\} c0′​={}。
• $f_{post}(o_i)$是应用于$o_i$的后处理变换，这也许涉及到神经网络层（例如情感分析），检查是否合规以及其他。尽管大部分现有方案的都不关注这个部分，我们期望在未来，后处理变换同样能够类似于预处理部分，涉及到脚本执行，访问网络，RAG等。
• ${\tilde{o}}_i$是LLM输出后处理的结果，${\tilde{o}}_i=f_{post}(o_i)$。
• $f_c,f{\prime }_c$ 是确定更新上下文的确切形式的转换。

3.3 Implementing Building Blocks

上述所提供的构建块可以作为在不同架构上有效实现提示基线的基础。例如，可以使用这些块的粒度来调度云服务中提示pipeline的不同部分：轻量级后处理 $f_{post}$ 可以作为快速功能实现，而 $f_{pre}$ 中的时间较长且有状态的 RAG 操作可以自动放置在 EC2。
　　$f_{pre}$、$LL{M}^X$、$f_{post}$ 和 $f_c$ 的详细信息取决于特定的 LLM 基础。一般来说，它们可用于实现生成式人工智能生态系统的不同部分。例如，大多数基于 RAG 的框架都会在 $f_{pre}$ 中实现 RAG。类似地，添加系统预提示可以作为$f_{pre}$的一部分来实现。 $f_c$ 中指定了如何更新上下文，或者当输入长度达到其限制时如何删除其某些部分的详细信息。
　　在许多情况下，用户有责任指定 $f_{pre}$、$f_{post}$、$f_c$ 的行为；例如，LLaMA 或使用 OpenAI API 时就是这种情况。相反，当与ChatGPT等商业服务交互时，这些变换是在LLM基础设施端定义和实现的。

4.ESSENCE OF REASONING TOPOLOGIES

现在，我们具体化了推理拓扑领域的不同概念，并将其与第 3 节中的一般提示流程和函数形式相关联。

4.1 What Is a Thought and a Reasoning Topology?

许多工作都使用“思维”这个词。然而，其确切含义可能会有所不同，具体取决于对应情况。例如，在 CoT 中，思维是指段落中的陈述，其中包含旨在解决输入任务的推理过程的一部分。我们在图 3 的顶部展示了这一点。在 ToT 中，在某些任务中，例如 24 字游戏，思维意味着初始问题的中间或最终解决方案。然而，在创意写作中，它可能是解决输入任务的计划，或者一段文本。在 GoT 中，思维包含输入任务（或其子任务）的解决方案。例如，它可以是要摘要的文档子集，或者是要排序的数字序列。
　　为了涵盖所有这些情况，我们将思维定义为解决任务的一个语义单元，即解决给定任务过程中的一个步骤。上面的所有例子都属于这个定义：解决任务的一个步骤可以是一个陈述、一个计划、一段文本、一组文档或一个数字序列。我们用节点来建模思维；节点之间的边对应于这些思维之间的依赖关系。这些依赖关系的详细信息也是特定于用例的。例如，在生成一段文本时，如果给定的段落$y$是先前版本$x$的精炼版本，则$x$和$y$成为拓扑中的节点，并且从$x$到$y$存在一条边，表明$y$依赖于$x$ 。如果任务是对数字序列进行排序，并且策略基于将序列拆分为子序列，独立排序并合并，则初始序列可以建模为节点$x$，子序列将 形成进一步的节点 $y,z,...$，具有从 $x$ 到建模子序列的所有节点的边 $(x,y),(x,z),...$。现在，推理拓扑是这些节点和边的图。
　　形式上，拓扑可以定义为 $G=(V,E)$，其中 $V$ 是一组建模思维的节点，$E$ 是这些节点之间的一组边，建模思维之间的推理依赖关系。这种对思想链、树和图进行推理的图论方法有助于设计更有效的推理方案。例如，当目标是最小化解决给定任务的延迟时，人们会尝试设计一种输入和输出节点之间距离较短的拓扑。

4.2 Semantic Roles of Thoughts & Topologies

图节点可以对推理的不同方面进行建模。例如，在写作任务中，一些节点对撰写段落的计划进行建模，而其他节点则对文本的实际段落进行建模。我们将这些方面称为不同的语义角色。正如在提示文献中已经观察到的那样，语义角色也可以用图论（即异构图）来建模。这使得能够利用强大的机制来进行新的LLM推理工作。例如，可以考虑在未来的提示方法中使用一些异构图学习方法。

4.3 Fundamental Use Cases of Thoughts & Topologies

我们确定了思维和拓扑的两个基本用例：上下文示例和引导我们找到解决方案的推理步骤。在思维拓扑中，如果存在从 $u$ 到 $v$ 的路径，则节点 $v$ 可以从另一个节点 $u$ 到达。如果从开始建模输入任务语句的节点可以到达节点 $v$，我们将这样的节点称为解决方案节点，并且对应的拓扑是解拓扑。然而，某些节点可能无法从输入节点到达。例如，用户可以（在他们的提示中）提供形成小拓扑的上下文示例，这不是解决输入任务的推理步骤，而仅仅是示例。我们将这种思维和拓扑称为上下文示例的思维和拓扑。这两个用例的示例可以在图 3 中找到。解决方案思维和拓扑用蓝色标记，而上下文示例用绿色标记。上下文示例的拓扑不会超出单个提示。另一方面，解决方案拓扑可以跨越许多提示和回复。
　　区分解决方案和上下文示例思维和拓扑可以实现更有效和高效的 LLM 推理方案。例如，图拓扑必须以某种方式表示。现在，使用上下文示例的拓扑通常仅限于单个提示，而解决方案拓扑通常超出单个提示或 LLM 响应，可以对这两个拓扑类使用不同的表示，以便最大限度地减少每个拓扑中的token利用率。
　　两种拓扑也可以共同建模为一张图，其中多个组件对应于彼此不连接的拓扑。为了进一步促进未来的优化，人们可以利用超顶点模型，其中任意子图都可以建模为称为超顶点的单个节点。在这样的视图中，人们可以将每个单独的上下文中样例拓扑建模为超顶点，与其他节点或具有超边的超顶点连接。可以利用这种方法来提供一个理论框架，用于优化推理方案的整体性能，包括其成分，例如与所有其他方案成分相关的上下文示例。

4.4 Functional Formulation of Reasoning Topologies

利用拓扑的 LLM 推理的表述方式与第 3 节中描述的完全相同。但是，必须考虑到通用情况下提示 $p_i$、回复 ${\tilde{o}}_i$ 和上下文 $c_i$ 的事实，它们都包含思维及其依赖关系。现在，拓扑映射到 $p_i$、${\tilde{o}}_i$ 和 $c_i$ 的确切方式取决于特定的提示方案。例如，在 CoT 的第 $i$ 个提示交互中，推理拓扑 $T$ 是 LLM 回复 ${\tilde{o}}_i$（当 $T$ 是解决方案拓扑时）或作为用户提示 $p_i$ 中上下文示例的子集（当 $T$ 是上下文示例的拓扑时）。 然而，在许多基于树和图的方案中，这种映射并不那么简单，并且拓扑可以跨越多个提示和回复。我们在图 3 中说明了这些示例。
　　在开发利用推理拓扑的 LLM 推理方案时，需要指定此类映射的细节，而且还需要构建该拓扑的表示、遍历拓扑的调度等。为了便于设计未来的LLM推理方案，我们现在提供了一个蓝图，清楚地定义了所有这些方面以及如何实例化它们。

4.5 A Blueprint for LLM Reasoning

　　我们确定了利用拓扑的 LLM 推理方案的以下基本方面： ❶ 拓扑类（LLM 推理中间步骤之间的连接结构，第 4.5.1 节）， ❷ 拓扑范围（拓扑和提示之间的映射/ 回复/上下文，第 4.5.1 节），❸ 拓扑表示（如何在提示/回复/上下文中表示给定拓扑，第 4.5.1 节），❹ 拓扑推导（如何获取给定拓扑，第 4.5.1 节） 、 ❺ 推理调度（如何遍历给定拓扑以进行 LLM 推理，第 4.5.2 节）、 ❻ 调度表示（如何在提示/思维中表示给定调度，第 4.5.2 节），以及 ❼ 利用部分 AI 管道（除了提示之外，使用了生成式 AI 管道的哪些部分，第 4.5.3 节）。我们在图 4 中描绘了蓝图，并根据该蓝图分析了现有方案，如表 1 所示。
　　提供的蓝图和分类适用于解决方案和上下文示例拓扑。例如，对单个上下文示例进行建模的拓扑可以有自己的表示、调度等。但是，为了清楚起见，我们将重点关注将蓝图和分类法主要应用于解决方案拓扑。

4.5.1 Topology of Reasoning

推理框架可以利用不同的拓扑来进行 LLM 推理过程。在这里，我们区分链、树和图。请注意，链和树都是连通图的特例：树是连通无向无环图，链是路径图（即每个节点最多有一个子节点的树）；请参见图 4 的第 ❶ 部分。尽管如此，我们还是将它们分开对待，因为它们对于不同的提示任务的有效性有所不同。在此视图下，普通 IO 提示可以被视为单节点图。
　　其次，我们观察到这些拓扑可以在单个提示或回复（单提示拓扑）中利用，也可以跨多个提示或回复（多提示拓扑）；参见图4第❷部分。
　　一个重要的方面是拓扑的表示，请参见图 4 的第❸部分。表示可以是隐式的（未显式指定节点和边）或显式的（显式指定节点和边）。显式表示各不相同，包括一组三元组或自然文本中节点和边的描述。隐式表示取决于方案 - 例如，它可能是规定生成下一个推理步骤的文本选项。最后，我们还确定了拓扑是如何推导的——例如，它可以由用户或 LLM 本身构建（图 4 的第❹部分）。具体来说，多提示拓扑的推导可以是手动的（在LLM推理之前由用户固定）、自动的（由LLM动态决定）或半自动的（整体推理结构在LLM推理开始之前预定义，但是 用户/LLM在实际推理过程中也对结构有一定的控制权）。

4.5.2 Reasoning Schedule

推理拓扑构成了 LLM 推理的“骨架”，有效地规定了解决给定任务的算法。然而，对于给定的固定拓扑，许多提示方案提供了不同的方法来执行中间推理步骤。例如，ToT 利用广度优先搜索 (BFS) 或深度优先搜索 (DFS)。这促使我们引入结构增强推理这另一维度，即推理调度。该调度规定了如何处理推理拓扑（图 4 的第❺部分）。
　　每当指定调度时，都可以用不同的方式表示（调度表示）。 它可以是自然语言的描述、代码规范、上下文示例或其他（图 4 的第❻部分）。最后，与拓扑一样，调度本身也可以使用不同的方法来确定，例如通过动态的 LLM，或预先确定（例如，作为固定的 BFS 调度）。

4.5.3 Beyond Prompting

许多方案超出了纯粹的LLM的提示范围。这可能包括预训练、微调、检索、工具或不同的模态（图 4 的第❼部分）。我们还考虑了这个方面，因为它提供了对推理拓扑与人工智能pipeline中其他机制的集成的见解，而不仅仅是简单的提示交互。

5.REASONING WITH CHAINS

我们现在继续更详细地研究使用链式拓扑的各个方案。我们根据表 1 顶部的分类法和蓝图分析这些工作（附录中提供了每个单独方案的详细描述）。我们还说明了这些工作中引入的基本概念，即多步推理、零样本推理、规划和任务分解、任务预处理、迭代优化和工具利用。我们通过比较分析并对样例拓扑表示进行说明来结束本节。

5.1 Multi-Step Reasoning

多步推理的概念首先通过开创性的思维链（CoT）引入，这是一种单提示方案，它使用上下文样例（也称为少样本样例）的拓扑来引导LLM在给出最终答案之前一步步推理。不同的后续工作增强或改编了上下文样例，以引发不同形式的推理步骤，同时仍然依赖于单提示链式拓扑。例如，SelfAsk 不仅仅在示例中提供逐步推理链，而是扩展了链中的每个步骤，以提出后续问题，然后在后续步骤中回答。类似地，Program of Thoughts (PoT) 使用代码样例，而不是像 CoT 那样使用基于自然语言的样例，来获得逐步生成的功能性 Python 程序，执行该程序可以获得最终结果。

5.2 Zero-Shot Reasoning Instructions

零样本推理指令旨在引出相同的多步骤推理链，但不需要使用手动选择的、特定于问题的上下文样例，即，它们消除了形成上下文样例的链式拓扑。Zero-shot-CoT 是 CoT 的扩展，只需用一句话“Let’s think step by step”或使用其他类似的陈述来提示LLM即可实现这一目标。同样，PoT 也可以利用零样本推理指令，例如“Let’s write a Python program step by step and return the result. Firstly we need to define the variables.”

5.3 Planning & Task Decomposition

规划和任务分解的目的都是将任务分解为许多可管理的子任务，以帮助达成最终解决方案。Plan-and-Solve (PS) Prompting 是基于此概念的关键单提示方案之一，它首先将复杂的任务划分为一系列子任务，然后逐步执行这些子任务以获得最终解决方案。PS 以零样本、多步骤的方式运行，因此也依赖于前两个概念。
　　规划和分解也经常用于多提示链中。在多提示推理链的开头引入用于指定分解细节的节点，通常不仅决定了链的深度，而且有利于后续子步骤中更有效的推理方法。这可以更细粒度地解决子任务，丰富整体推理过程。其中，Least-to-Most Prompting 形成了一条推理链，其中复杂任务或问题的分解在第一个节点中进行，子任务/子问题在后续节点中解决。具体来说，多提示链的运行方式是首先将原始问题分解为子问题列表，每个子问题都在单独的子步骤中解决，并在上下文中包含先前子步骤的问题和答案。当回答列表中的所有子问题都返回最终答案时，链式终止。然后，Decomposed Prompting是一个模块化框架，用于对复杂任务进行详细分解。为了生成推理链，LLM通过由顺序排列的问题操作三元组来进行提示，这些三元组形成“子问题”。与 Least-to-Most的提示相反，这允许将问题递归分解为更简单的子问题，直到可以直接解决它们，因为进一步分解是框架中的有效操作。除了上述两种方案之外，分解在许多类似的工作中也得到应用。

5.4 Task Preprocessing

任务预处理的概念包括在采取任何推理步骤之前通过更新任务描述或重新表述任务描述本身来预处理任务上下文的任何技术。例如，多提示方案Selection-Inference (SI)旨在解决多步骤逻辑推理问题，其中所有基本信息已经存在于输入上下文中。SI 的关键功能在于其在每个推理步骤之前反复进行上下文修剪的过程。这意味着它有选择地过滤上下文，仅保留每个特定后续推理步骤所需的相关信息，确保每个决策阶段始终使用最相关的数据。另一方面，专为空间规划任务设计的多提示方案 Chain-of-symbol (CoS) 不是修剪上下文，而是用压缩的符号表示来增强上下文，然后再使用这些作为提示来帮助LLM进行基于 CoT 的推理。

5.5 Iterative Refinement

验证的引入使推理框架能够迭代地细化生成的上下文和中间结果。通过这种策略，基于链的推理的执行可以通过循环有效地扩展，条件是可以在节点上循环多少次（基于迭代次数或某些终端条件）。这个概念被应用在不同的工作中。

5.6 Tool Utilization

为了更好地集成多种执行方法，更有效的方案选择在执行推理链之前制定一个计划，指定用于处理每个子任务的工具。 示例包括 AutoGPT、Toolformer、Chameleon、ChatCot、PVS 等。

5.7 Analysis & Comparison of Designs

我们现在根据蓝图的不同方面广泛讨论和分析链设计。

5.7.1 Topology & Its Construction

在单提示方案中，整个推理过程在单提示轮次内执行。这种方法对于复杂任务来说不太常见，因为它通常需要复杂的提示工程来一次性涵盖整个推理路径。另一方面，大多数链式设计采用多提示方案，将推理过程分为多轮提示。这允许采用更加细致和逐步的方法来解决问题。链设计的新架构特征包括适当分解任务、验证和完善中间解决方案、预处理初始提示以及利用外部工具（例如 Python 脚本）的能力。这种多方面的方法使LLM能够通过将问题分解为更小、更易于管理的组件并迭代地完善解决方案来解决更复杂的问题。

5.7.2 Representations of Topology & Schedule

　　我们现在说明代表性提示，这些提示显示了基于单提示和多提示链的拓扑之间的差异（这些任务在附图的提示中详细描述）。我们使用的示例是 24 字游戏、创意写作以及数学或逻辑推理等众所周知的任务。为此，我们在图 5 中说明了一个最简单的 IO 方案示例（实际上是单节点 CoT），并将其与图 6 中的隐式单提示few-shot CoT、图 7 中的隐式单提示zero-shot CoT 和 图 8 中的显式多提示few-shot CoT（选择推理）示例进行了比较。

5.7.3 Performance

我们现在总结链式拓扑中发现的性能模式。更详细的性能比较，请参见附录 E.1。
　　总体而言，在算术推理中，CoT 显着优于输入输出 (IO) 提示，在例如 GSM8K（小学数学）、SVAMP（算术数学应用题的简单变体）和 MAWPS（数学应用题）等数据集中具有显著的性能提升。CoT 的有效性随着LLM规模的扩大而提高。 Zero-shot-CoT、PoT 等变体以及具有分解节点的方案（如从Least-to-Most提示、PS+）显示了特定数据集的进一步改进。Chameleon 及其表格阅读器工具可提高表格数学问题的表现。
　　在常识推理中，CoT 优于 IO 提示，在 StrategyQA 等数据集中具有明显的优势。SelfAsk 和选择推理框架等专业方法显示了多跳问题的进一步改进。基于分解的方案（例如从Least-to-Most和分解提示）可以在需要顺序操作或多方面推理的任务中实现高精度。ChatCoT 凭借其检索和外部工具利用率，在特定数据集上显示出 20% 的增益。
　　在符号推理中，CoT 在上下文示例中表现出近乎完美的准确性，在领域外案例中表现出极高的准确性，例如最后一个字母串联和硬币翻转预测等任务。在更复杂的任务和更长的单词场景中，具有分解节点的方案优于 CoT。
　　总体而言，在不同领域，CoT 及其变体表现出优于基本 IO 提示的一致趋势。附加工具的集成、定制的提示策略（例如少样本或零样本）以及分解和细化节点的结合显着提高了LLM的性能。

6.REASONING WITH TREES

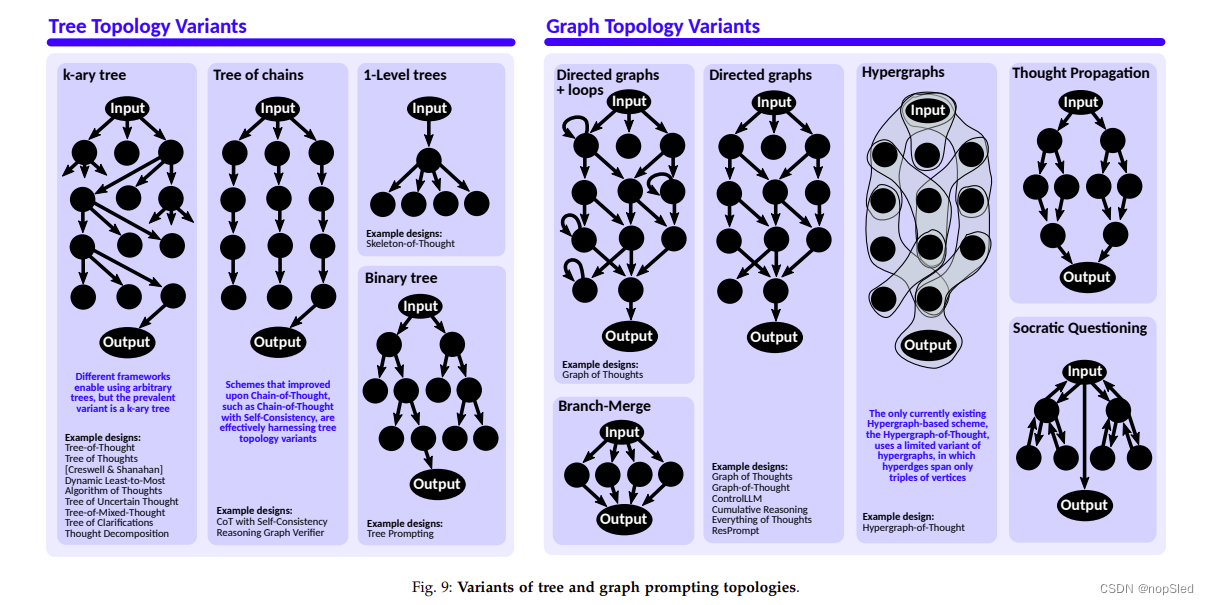
　　接下来我们更详细地研究使用树拓扑的各个方案。我们根据表 1 中间部分的蓝图和分类法分析这些工作（附录中提供了每个单独方案的详细描述）。我们根据所利用的拓扑变体（即链式树、1–level 树和 k–ary 树）构建讨论，详细信息请参见图 9。与链式方案一样，我们还讨论了这些工作中引入或利用的基本概念。最重要的是，树形方案引入了探索（即从给定的思维中产生多种思维）。树形方案中探索背后的目标通常是任务分解（与 CoT 类似，但不同之处在于分解不限于单个线性计划）或采样（即有更高的机会获得高质量的解决方案）。此外，树方案还引入了投票（即自动选择所有生成的输出的最佳结果），并且它们利用了链式方案中也使用的各种架构概念，例如迭代细化或任务预处理。我们通过比较分析和示例拓扑表示的说明来结束本节。

6.1 Trees of Chains

虽然 Long [133] 和 Yao [213] 的工作中明确建立了树作为推理拓扑，但这种想法很早就已经出现。具有自洽思维链（CoT-SC）是一种在一定程度上利用树结构的早期方案。在这里，多个 CoT 源自同一个初始（根）提示符，形成“链式树”。 为初始问题提供最佳结果的链被选择作为最终答案。

6.2 Single-Level Trees

基于树的方法也被用于Skeletonof-Thought (SoT)，它有效地利用了单一深度级别的树。该方案旨在减少 LLM 由其固有的顺序解码引起的端到端生成延迟。该方案没有生成一个长的连续答案，而是使用分而治之的方法。在第一个提示中，LLM被指示生成答案的框架，即独立回答的点列表。然后，对于每一点，都会并行发出一个新提示来回答问题的这个特定部分。由于这些点是并行处理的，因此总体延迟会减少。

6.3 k–Ary Trees

许多计划都利用了更多的通用 k–Ary 树。首先，Tree-of-Thought (ToT) design by Long [133] 利用树结构将问题分解为子问题，并使用单独的 LLM 提示来解决它们。在 LLM 建议可能的后续步骤和相应的部分解决方案后，检查器模块会决定这些解决方案中的任何一个是否有效，是否可以选择它作为最终解决方案，或者是否应该回溯到上一步。所有发出的提示和答案都明确存储为树结构，并使用控制器模块进行导航。LLM 提示仅用于生成该树中的下一个单独步骤（即hop），而整个问题解决过程由控制器协调。
　　Tree of Thoughts (ToT) by Yao et al. [213] 与上述 ToT 方法的不同之处在于使用 LLM 本身作为解决方案评估器，可以访问所有生成的解决方案，而不是使用编程或学习的评估器模块。这允许对状态进行单独评级或对中间解决方案进行投票，以选择最有希望的一个来继续搜索。提到的两种 ToT 方法都是 IO、CoT 和 CoT-SC 提示方案的推广。
　　此类拓扑中的其他示例包括Thought Decomposition（这是一种基于随机集束搜索和自评估的多提示方案）、Creswell and Shanahan [50] 的方案（基于链的选择推理的扩展）、Dynamic Leastto-Most Prompting（通过基于树的问题分解和动态的基于树的外部少量示例选择来扩展从最少到最多的提示）、Algorithm of Thoughts (AoT)（一种利用上下文示例的以基于算法树的方式制定的单提示方法）、Tree of Uncertain Thought (TouT)（通过将多个 LLM 响应的方差纳入状态评估函数，对 ToT 进行局部“不确定性分数”的扩展）、Tree-of-MixedThought (TomT)（一种基于 ToT 的推理方案，用于回答有关视觉场景图的问题），或Tree of Clarifications (ToC) （递归提示LLM为初始问题构建消歧树）。

6.4 Analysis & Comparison of Designs

我们现在根据蓝图的不同方面广泛讨论和分析树的设计。

6.4.1 Topology & Its Construction

树形方案这一新架构的关键特征是对思维的探索，即基于给定的单个步骤生成多个新步骤的能力。 绝大多数树方案都是多提示的。大多数多提示方案使用动态方法来构建树形拓扑。拓扑如何精确成形的细节取决于具体问题。对于大多数多提示方法，用户可以在一定程度上调整树拓扑，即通过改变分支因子（即从给定顶点生成思维的数量）并限制树的深度。

6.4.2 Representations of Topology & Schedule

　　我们使用代表性示例展示了隐式与显式以及单提示拓扑与多提示拓扑之间的差异（这些任务在图片的提示中详细描述）。我们继续来完成 24 字游戏、创意写作和数学/逻辑推理等任务。为此，我们在图 10 中说明了由 AoT 引发的隐式单提示树拓扑，以及分别在图 11 和 12 中说明了来自 ToT 和 CoT-SC 的两个示例显式多提示树拓扑。最后，我们展示了一个示例 图 13 中 SoT 的并行执行计划。

6.4.3 Performance

我们现在总结树拓扑中发现的性能模式。 详细分析参见附录 E.2。
　　总体而言，增加分支因子（即从给定顶点生成思维的数量）通常会导致结果的多样性更高，这可能有利于准确性，但它也会增加#prompts，即计算成本。最有利的分支因子很难找到，并且通常取决于要解决的具体问题。与复杂问题相比，容易分解的问题可能从更多分支中获益较少。具体来说，更复杂的问题通过将其分解为许多/多样化的子问题而获益更多（例如，这确保了足够的多样性以实现更好的自洽）。相反，显然只有两个子部分的问题不会从更多的细分中受益，因为附加的分支可能是多余的或错误的。单提示方法在某些问题上的表现比多提示方法更好，而仅使用单个提示与可能使用数百个提示相比。

7. REASONING WITH GRAPHS

我们还分析了利用图拓扑的方案，请参见表 1 的底部部分（附录中提供了每个单独方案的详细描述，如链和树）。与树分析类似，我们根据所利用的拓扑变体构建讨论，详细信息请参见图 9。我们还讨论了这些工作中引入或利用的基本概念。最重要的是，图方案引入了聚合（即能够将多个思维组合成一个）。聚合背后的目的通常是协同作用（即能够产生比单个成分更好的结果）或任务结果的有效组合。图方案还使用链或树方案中采用的架构概念，例如探索或迭代细化。我们通过比较分析和图拓扑示例表示的说明来结束本节。

7.1 Special Classes of Graphs

不同的方案利用某些特殊类别的图。Branch-Solve-Merge (BSM) 采用1层双树结构，首先将问题划分为可独立求解的子问题，然后将它们组合成最终的解决方案。第一个提示用于提示LLM提出子问题，然后独立解决这些子问题。最后的提示指示 LLM 将子问题的结果合并为单个输出。Socratic Questioning 是一种使用树结构对思维空间进行递归探索的方案。由此，原始问题被递归地分解为子任务，直到所有任务都能以高置信度得到解决。然后，这些结果被聚合并传播回树以回答原始问题。这导致整体双树推理拓扑。

7.2 Directed Graphs

一些方案采用通用有向图模型。Graph of Thoughts (GoT) [10] 使用多提示方法，通过将给定任务分解为形成图的子任务来提高 LLM 问题解决性能。该分解被指定为 Graph of Operations (GoO)。GoO 协调如何提示 LLM 以及如何在推理过程中进一步使用结果。**Graph of Thoughts (GoT) [119]**提出了一种多提示方法，其中从代表LLM要回答的问题的问题节点开始，以 DFS 方式递归构建思维图。从该节点开始，LLM 生成可能的推理路径。对于每条路径，LLM 都会生成新节点（即中间推理步骤），然后用于生成图。Graph of Thoughts (GoT) [215] 描述了一个两阶段框架来回答多模态问题，即伴随图像的文本问题。在第一阶段，模型根据输入文本生成自然语言原理，提供额外的上下文和知识来支持回答给定的问题。 这个基本原理的生成是作为整个模型管道的一部分来学习的。在第二阶段，这些基本原理被附加到初始问题中，并再次通过模型来预测答案。此类中的其他方案包括Cumulative Reasoning、Everything of Thoughts (XoT)、ControlLLM 和 ResPrompt。

7.3 Hypergraphs

最后，我们还考虑 Hypergraphs，它通过使边能够连接节点的任意子集而不是仅仅两个节点之间的链接来泛化图。我们将超图纳入分类法，因为初步工作已经利用它们进行多模态提示。这里，**Hypergraph-of-Thought (HoT) [212]**是一种将思维过程建模为超图的多模态推理范式。首先，构建一个如[215]中的思维图。 然后构建共享相同节点的文本超图。然后将超边定义为节点三元组，例如“(Lionel Messi, place of birth, Rosario)”。此外，视觉超思维图是通过对图像块执行 k 均值聚类来构建的，其中一个聚类对应于一个超边。然后对两个超图进行编码并组合以执行图学习。

7.4 Analysis & Comparison of Designs

8.CHAINS VS. TREES VS. GRAPHS OF THOUGHTS

9.DESIGN ARCHITECTURES