Token-level Direct Preference Optimization翻译

摘要

对预训练的大型语言模型 (LLM) 进行微调对于使其与人类价值观和意图保持一致至关重要。此过程通常使用成对比较和与参考 LLM 进行 KL 散度等方法，重点是评估模型生成的完整答案。但是，这些响应的生成发生在 token 级别，遵循顺序、自回归的方式。在本文中，我们介绍了 Token 级直接偏好优化 (TDPO)，这是一种通过在 token 级别优化策略使 LLM 与人类偏好保持一致的新方法。与以前面临散度效率挑战的方法不同，TDPO 为每个 token 合并了前向 KL 散度约束，从而提高了对齐和多样性。利用 Bradley-Terry 模型作为基于 token 的奖赏系统，TDPO 增强了 KL 散度的调节，同时保持了简单性，而无需显式的奖赏建模。在各种文本任务的实验结果表明，TDPO 在平衡对齐与生成多样性方面表现出色。值得注意的是，在可控情感生成和单轮对话数据集中，使用 TDPO 进行微调比 DPO 取得了更好的平衡，并且与基于 DPO 和 PPO 的 RLHF 方法相比，生成的响应质量显著提高。我们的代码已在 https://github.com/Vance0124/Tokenlevel-Direct-Preference-Optimization 上开源。

1.介绍

　　大型语言模型 (LLM) 已在各种领域展现出显著的泛化能力，包括文本摘要、代码编写，甚至遵循人类指令。为了使 LLM 与人类意图保持一致，来自人类反馈的强化学习 (RLHF) 已成为一种非常有效的方法，体现了风格和道德价值观。这些方法通常涉及奖赏模型的训练，然后使用强化学习 (RL) 对策略模型进行微调。
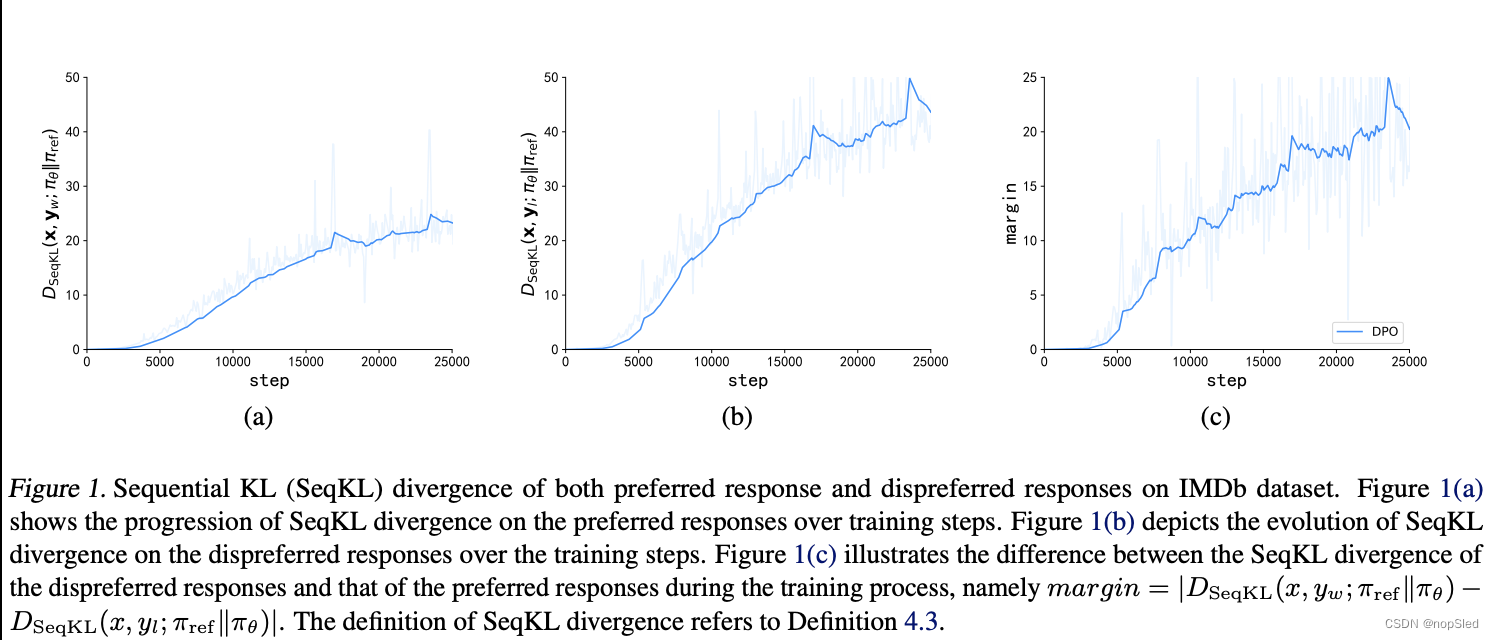
　　直接偏好优化 (DPO) 引入了一种直接有效的技术，使用成对比较来训练 LLM，而无需明确建立奖赏模型。DPO 利用 KL 散度来确保训练过程与参考大型语言模型 (LLM) 保持紧密一致，从而防止出现重大偏差。在 DPO 中，KL 散度是在句子级别进行评估的，这反映了评估基于完整的响应（答案），通常一个响应中包含几个句子。但是，这些响应的生成是按顺序进行的，遵循自回归方法。一个潜在的好处是可以更细致地逐个token地检查与参考 LLM 相关的散度。一种方法是使用序列 KL 散度（如定义 4.3 中所定义），它监视生成的响应的轨迹。如图 1 所示，与优选响应子集相比，DPO 在非优选响应子集中的 KL 散度增加速度明显更快。这导致两个子集之间的差距不断扩大，也表明 DPO 无法有效控制非优选响应子集的 KL 散度。这会影响模型的散度效率，并最终影响其语言能力和生成多样性。这种限制凸显了在 DPO 框架内使用 KL 散度的有效性下降，表明其方法论存在改进空间。
　　连续 KL 散度增长率的不平衡可能与 DPO 所采用的反向 KL 散度约束有关。反向 KL 散度的模式寻求特性往往会导致生成过程中的多样性降低，从而限制模型产生多样化和有效响应的潜力。基于 DPO 的 f-DPO 方法研究了不同散度约束下 LLM 的对齐性能和生成多样性之间的权衡。它强调了前向 KL 散度的质量覆盖行为在增强模型多样性方面的优势，并探讨了不同散度约束的影响。然而，f-DPO 仅独立讨论了在反向 KL 散度或前向 KL 散度约束下模型行为的变化。本质上，它并没有从根本上增强 DPO 算法本身，而是通过简单地交换不同的 KL 散度约束来在对齐性能和生成多样性之间取得平衡。
　　受上述观察的启发，我们从序列和 token 级别的角度定义和研究了与人类偏好对齐的问题。在这个方向上也有一些并行的工作。我们引入了一种新方法，称为 Token 级直接偏好优化（TDPO），旨在通过控制每个 token 的 KL 散度在对齐性能和生成多样性之间取得更好的平衡。为了实现这一点，我们重新定义了以序列方式最大化限制性奖赏的目标。使用贝尔曼方程建立了句子级奖赏和 token 级生成之间的联系。之后，Bradley-Terry 模型被转换为 token 级别的表示，证明了它与 Regret Preference Model 的密切关系。通过利用这种方法，我们在最终的目标函数中有效地集成了每个 token 的前向 KL 散度限制，从而改善了 KL 散度的调节。
　　TDPO 保留了 DPO 的简单性，同时提供了改进的 KL 散度调节，以使 LLM 与人类偏好保持一致。与 DPO 的策略相呼应，我们的方法直接优化策略，而无需在整个训练阶段进行显式奖赏模型学习或策略采样。我们的实验结果证明了 TDPO 在多个文本任务中的有效性，并且与基于 DPO 和 PPO 的 RLHF 方法相比，生成的响应质量得到了显着提升。总之，TDPO 不仅能够有效解决 KL 散度过大的问题，而且还能大大提高散度效率，因此脱颖而出。

2.Related Works

ChatGPT 的出现催化了大型语言模型 (LLM) 领域的重大进步，例如 OpenAI 的 GPT-4、Mistral 和 Google 的 Gemini。一般来说，LLM 的训练包括三个阶段：最初在海量文本语料库上进行无监督预训练以掌握语言结构，然后使用特定于任务的数据集进行有监督微调以提高 LLM 产生所需响应的概率。然而，由于在有监督微调阶段标记数据集的可用性通常有限且昂贵，该模型可能会保留偏见和不准确性，表现为社会偏见、道德问题、毒性和幻觉，这需要后续的 AI 校准阶段。Zephyr 和 GPT-4 等实现显著校准的值得注意的模型已经证明了从人类反馈进行强化学习 (RLHF) 和直​​接偏好优化 (DPO) 算法等技术的有效性。
　　基于人类反馈的强化学习 (RLHF) 已成为 LLM 与人类价值观相对齐的基石，提供了一种基于定性反馈来优化模型输出的机制。这种方法通过人类反馈迭代改进模型性能，在使得模型在符合人类期望和道德考虑方面表现出了巨大的潜力。然而，实现 RLHF 的复杂性，加上人类生成的奖赏模型的不准确性，促使人们探索替代策略。奖赏排名微调 (RAFT) 和排名响应以对齐人类反馈 (RRHF) 等方法提供了简化的对齐方法，规避了 RLHF 的一些固有挑战。特别是，直接偏好优化 (DPO) 代表了直接策略优化的突破，通过细粒度的奖赏函数优化方法解决了平衡模型行为的复杂性。然而，在符合人类偏好的同时保持语言多样性的挑战仍然是一个关键关注点，这促使我们提出了 Token 级直接偏好优化 (TDPO)，旨在协调模型输出中的对齐准确性和表达范围的双重目标。

3.Preliminaries

对于语言生成，语言模型 (LM) 会根据提示（问题）$x$ 生成响应（答案）$y$，其中 $x$ 和 $y$ 均由一系列token组成。直接偏好优化 (DPO) 从 RLHF 的 RL 目标开始：
$$\underset{{\pi }_{\theta }}{\max }{\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(\cdot |x)}[r(x,y)-\beta D_{KL}({\pi }_{\theta }(\cdot |x)||{\pi }_{ref}(\cdot |x))],\text{\hspace{1em}(1)}$$
其中 $\mathcal{D}$ 表示人类偏好数据集，$r(x,y)$ 表示奖赏函数，${\pi }_{ref}(\cdot |x)$ 作为参考模型，通常选择有监督微调后的语言模型，${\pi }_{\theta }$ 表示进行 RL 微调的模型，用 ${\pi }_{\theta }={\pi }_{ref}$ 初始化，$\beta$ 是反向 KL 散度惩罚的系数
　　通过直接推导等式1，DPO在逆KL散度下建立了奖赏模型与最优策略之间的映射，得到了关于策略的奖赏函数的表示：
$$r(x,y)=\beta log\frac{{\pi }_{\theta }(y|x)}{{\pi }_{ref}(y|x)}+\beta logZ(x).\text{\hspace{1em}(2)}$$
这里，$Z(x)$ 是配分函数。
　　为了符合人类偏好，DPO 使用 BradleyTerry 模型进行成对比较：
$$P_{BT}(y_1\succ y_2|x)=\frac{exp(r(x,y_1))}{exp(r(x,y_1))+exp(r(x,y_2))}.\text{\hspace{1em}(3)}$$
　　通过将公式 2 代入公式 3 并利用负对数似然损失，DPO 得出目标函数：
$$\begin{array}{c}u(x,y_w,y_l)=\beta log\frac{{\pi }_{\theta }(y_w|x)}{{\pi }_{ref}(y_w|x)}-\beta log\frac{{\pi }_{\theta }(y_l|x)}{{\pi }_{ref}(y_l|x)},\\ {\mathcal{L}}_{DPO}({\pi }_{\theta };{\pi }_{ref})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[log\sigma (u(x,y_w,y_l))],\end{array}\text{\hspace{1em}(4)}$$
并且导数如下所示：
$${\nabla }_{\theta }{\mathcal{L}}_{DPO}({\pi }_{\theta };{\pi }_{ref})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[\sigma (-u){\nabla }_{\theta }u],\text{\hspace{1em}(5)}$$
其中 $u$ 是 $u(x,y_w,y_l)$ 的缩写，$y_w$ 和 $y_l$ 表示偏好和非偏好响应。

4.Methodology

在本节中，我们首先将有KL散度约束的奖赏最大化问题重新表述为 token 级形式。由此，我们推导出状态-动作函数与最优策略之间的映射。随后，我们将 Bradley-Terry 模型转换为 token 级表示，建立其与遗憾偏好模型的等价性。通过将映射关系代入 token 级的奖赏模型，我们得到仅与策略相关的优化目标。最后，我们对该优化目标进行导数形式化分析，并在此基础上推导出 TDPO 的最终损失函数。

4.1 Markov Decision Process under Token Rewards

为了对连续的自回归生成进行建模，我们扩展了第 3 节中的句子级公式，认为响应由 $T$ 个token $y=y^{<T+1}:=[y^1,y^2,...,y^T]$ 组成，其中 $y^t\in \mathcal{Y}$，$\mathcal{Y}$ 代表字母表（词表）。此外，我们假设 $y^{<1}=[]$。给定提示 $x$ 和响应 $y$ 的前 $t-1$ 个token $y^{<t}$，LM 预测下一个token的概率分布 ${\pi }_{\theta }(\cdot |[x,y^{<t}])$。
　　当将文本生成建模为马尔可夫决策过程时，状态是提示$x$和到当前步骤为止生成的响应的组合，表示为 $s_t=[x,y^{<t}]$。动作对应于下一个生成的token，表示为 $a_t=y^t$，并且token奖励定义为 $R_t:=R(s_t,a_t)=R([x,y^{<t}],y^t)$。
　　扩展所提供的定义，我们为策略 $\pi$ 建立状态动作函数 $Q_{\pi }$、状态价值函数 $V_{\pi }$ 和优势函数 $A_{\pi }$：
$$\begin{array}{c}{Q}_{\pi }([x,y^{<t}],y^t)={\mathbb{E}}_{\pi }[{\sum }_{k=0}^{\infty }{R}_{t+k}|s_t=[x,y^{<t}],a_t=y^t],\\ V_{\pi }([x,y^{<t}])={\mathbb{E}}_{\pi }[Q_{\pi }([x,y^{<t}],y^t)|s_t=[x,y^{<t}]],\\ A_{\pi }([x,y^{<t}],y^t)=Q_{\pi }([x,y^{<t}],y^t)-V_{\pi }([x,y^{<t}]).\end{array}\text{\hspace{1em}(6)}$$
其中，$\gamma$ 表示衰减因子。本文取 $\gamma =1$。

4.2 Token-Level Optimization

公式 1 中的 DPO 目标函数在句子级别运行。相比之下，我们提出了另一种 token 级别的目标函数：
$$\underset{{\pi }_{\theta }}{\max }{\mathbb{E}}_{(x,y^{<t})\sim \mathcal{D},z\sim {\pi }_{\theta }(\cdot |[x,y^{<t}])}[A_{{\pi }_{ref}}([x,y^{<t}],z)-\beta D_{KL}({\pi }_{\theta }(\cdot |[x,y^{<t}])||{\pi }_{ref}(\cdot |[x,y^{<t}])).\text{\hspace{1em}(7)}$$
　　该目标函数的灵感来自信赖区域策略优化 (TRPO)。如引理 4.1 所示，最大化等式 7 中的目标函数将导致期望回报方面的策略改进。
　　Lemma 4.1 给定两个策略 $\pi$ 和 $\tilde{\pi }$，如果对于任何状态 $s_t=[x,y^{<t}]$，${\mathbb{E}}_{z\sim \tilde{\pi }}[A_{\pi }([x,y^{<t}],z)]\ge 0$，那么我们可以得出结论：
$${\mathbb{E}}_{x\sim \mathcal{D}}[V_{\tilde{\pi }}([x])]\ge {\mathbb{E}}_{x\sim \mathcal{D}}[V_{\pi }([x])],$$
证明见附录 A.1。
　　值得注意的是，为了保持生成多样性并防止模型破解一些高奖赏答案，我们在 token 级目标函数中为每个 token 加入了反向 KL 散度，这防止模型偏离参考模型分布太远。
　　从公式7中的token级目标函数出发，我们可以直接推导出状态动作函数$Q_{\pi }$与最优策略${\pi }_{\theta }^{\ast }$之间的映射。我们在以下引理中总结了这种关系。
　　Lemma 4.2 公式 7 中的约束问题有闭式解：
$${\pi }_{\theta }^{\ast }(z|[x,y^{<t}])=\frac{{\pi }_{ref}(z|[x,y^{<t}])exp(\frac{1}{\beta }{Q}_{{\pi }_{ref}}([x,y^{<t}],z))}{Z([x,y^{<t}];\beta )},\text{\hspace{1em}(8)}$$
其中$Z([x,y^{<t}];\beta )={\mathbb{E}}_{z\sim {\pi }_{ref}(\cdot |[x,y^{<t}])}{e}^{\frac{1}{\beta }{Q}_{{\pi }_{ref}}([x,y^{<t}],z)}$是配分函数。
　　更多详细信息请参阅附录 A.2。
　　为了从公式 8 得到最优策略 ${\pi }_{\theta }^{\ast }$，我们必须估计状态-动作函数 $Q_{{\pi }_{ref}}$ 和配分函数 $Z(\cdot )$。然而，准确估计状态-动作函数 $Q_{\pi }$ 在每个状态和动作上的准确性具有挑战性，估计配分函数 $Z(\cdot )$ 也很困难。因此，我们重新整理公式 8，得到状态动作函数在策略方面的表达式：
$$Q_{ref}([x,y^{<t}],z)=\beta log\frac{{\pi }_{\theta }^{\ast }(z|[x,y^{<t}])}{{\pi }_{ref}(z|[x,y^{<t}])}+\beta logZ([x,y^{<t}];\beta ).\text{\hspace{1em}(9)}$$

4.3 BT Model Reformulation via Advantage Function

为了方便后续推导，我们首先引入连续 KL 散度，其定义见 Definition 4.3。
　　Definition 4.3。给定两个语言模型 ${\pi }_1$ 和 ${\pi }_2$，输入提示 $x$ 和输出响应 $y$，连续 KL 散度定义为：
$$D_{SeqKL}(x,y,{\pi }_1||{\pi }_2)=\sum _{t=1}^T{D}_{KL}({\pi }_1(\cdot |[x,y^{<t}])||{\pi }_2(\cdot |[x,y^{<t}])).\text{\hspace{1em}(10)}$$
　　给定提示 $x$ 和成对的回答 $(y_1,y_2)$，Bradley-Terry 模型表达了人类的偏好概率。然而，由于 Bradley-Terry 模型是在句子级别上表述的，因此无法与公式 9 中给出的 token 级别映射建立联系。因此，我们需要推导出 token 级别的偏好模型。从 Bradley-Terry 模型出发，我们将其转化为 token 级别的表述，并证明其与遗憾偏好模型的等价性，如引理 4.4 所示。
　　Lemma 4.4。给定一个奖赏函数 $r(x,y)$，假设 token 级奖赏与奖励函数之间的关系为 $r(x,y)={\sum }_{t=1}^T{\gamma }^{t-1}R([x,y^{<t}],y^t)$，我们可以在文本生成对齐任务中建立 Bradley-Terry 模型与遗憾偏好模型之间的等价性，即：
$$P_{BT}(y_1\succ y_2|x)=\sigma (\sum _{t=1}^{T_1}{\gamma }^{t-1}{A}_{\pi }([x,y_1^{<t}],y_1^{<t})-\sum _{t=1}^{T_2}{\gamma }^{t-1}{A}_{\pi }([x,y_2^{<t}],y_2^{<t})),\text{\hspace{1em}(11)}$$
其中 $\sigma (x)=1/(1+exp(-x))$ 是sigmoid函数。
　　我们在附录A.3中证明了这个引理。
　　在引理 4.4 中，我们假设 $r(x,y)={\sum }_{t=1}^T{\gamma }^{t-1}R([x,y^{<t}],y^t)$。这个假设在 RL 的背景下是自然的，其中 $r(x,y)$ 表示在给定提示 $x$ 的情况下对 $y$ 的响应的总体奖励。将文本生成视为一个序列决策问题，$r(x,y)$ 可以看作是生成文本的累积奖励。
　　根据 4.1 节中优势函数的定义，我们可以直接建立式 9 中的最优解与式 11 中的偏好优化目标之间的关系。一个难点是状态动作函数 $Q_{\pi }$ 依赖于一个配分函数，而该配分函数既取决于输入提示 $x$，又取决于输出响应 $y^{<t}$。这会导致一对响应 $(y_w,y_l)$ 的配分函数值不相同，具体为 $Z([x,y_w^{<t}];\beta )\ne Z([x,y_l^{<t}];\beta )$。因此，我们不能采用类似于 DPO 的取消策略，该策略依赖于 Bradley-Terry 模型仅取决于两次补全之间的奖赏差异的属性。
　　幸运的是，通过扩展优势函数 $A_{\pi }$ 并将状态价值函数 $V_{\pi }$ 转换为仅与状态动作函数 $Q_{\pi }$ 相关的形式，我们可以自然地抵消配分函数。通过这种方式，我们最终将 Bradley-Terry 模型重新表述为直接与最优策略 ${\pi }_{\theta }^{\ast }$ 和参考策略 ${\pi }_{ref}$ 相关。这总结在以下定理中。
　　Theorem 4.5。在对应于式7的KL约束优势函数最大化问题中，Bradley-Terry模型用最优策略${\pi }_{\theta }^{\ast }$和参考策略${\pi }_{ref}$来表达人类偏好概率：
$$P_{BT}^{\ast }(y_1\succ y_2|x)=\sigma (u^{\ast }(x,y_1,y_2)-{\delta }^{\ast }(x,y_1,y_2)),\text{\hspace{1em}(12)}$$
其中，$u(x,y_1,y_2)$ 表示语言模型 ${\pi }_{\theta }$ 和参考模型 ${\pi }_{ref}$ 隐式定义的奖赏差异，表示为：
$$u(x,y_1,y_2)=\beta log\frac{{\pi }_{\theta }(y_1|x)}{{\pi }_{ref}(y_1|x)}-\beta log\frac{{\pi }_{\theta }(y_2|x)}{{\pi }_{ref}(y_2|x)},\text{\hspace{1em}(13)}$$
并且 $\delta (x,y_1,y_2)$ 表示两对 $(x,y_1)$ 和 (x, y_2) 之间的连续前向 KL 散度差，以 $\beta$ 加权，表示为：
$$\delta (x,y_1,y_2)=\beta D_{SeqKL}(x,y_2;{\pi }_{ref}||{\pi }_{\theta })-\beta D_{SeqKL}(x,y_1;{\pi }_{ref}||{\pi }_{\theta }).\text{\hspace{1em}(14)}$$
　　证明见附录A.4。

4.4 Loss Function and Formal Analysis

　　基于公式 12，我们将 Bradley-Terry 模型重新表述为仅与策略相关的结构。这使我们能够为参数化策略 ${\pi }_{\theta }$ 制定似然最大化目标，从而推导出我们方法初始版本的损失函数 $TDP{O}_1$：
$${\mathcal{L}}_{TDP{O}_1}({\pi }_{\theta }^{\prime }{\pi }_{ref})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[log\sigma (u(x,y_w,y_l)-\delta (x,y_w,y_l))].\text{\hspace{1em}(15)}$$
　　通过这种方法，我们显式地将顺序前向 KL 散度引入损失函数。再加上隐式集成的反向 KL 散度，我们增强了平衡 LLM 对齐性能和生成多样性的能力。
　　随后，我们对该方法进行导数分析，并对 TDPO 的损失函数进行具体修改。为方便起见，我们使用 $u$ 表示 $u(x,y_w,y_l)$，使用 $\delta$ 表示 $\delta (x,y_w,y_l)$。利用公式 15 中给出的损失函数公式，我们计算损失函数关于参数 $\theta$ 的梯度：
$${\nabla }_{\theta }{\mathcal{L}}_{TDP{O}_1}({\pi }_{\theta };{\pi }_{ref})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[\sigma (-u+\delta )[{\nabla }_{\theta }u-{\nabla }_{\theta }\delta ]].\text{\hspace{1em}(16)}$$
　　在等式 16 中，$\sigma (-u+\delta )$ 是梯度的权重因子。第一部分 $(-u)$ 对应于 DPO 损失函数中的权重因子。当语言模型在预测人类偏好时出错时，即 $log\frac{{\pi }_{\theta }(y_l|x)}{{\pi }_{ref}(y_l|x)}>log\frac{{\pi }_{\theta }(y_w|x)}{{\pi }_{ref}(y_w|x)}$，$(-u)$ 的值将变得更大，对响应对 $(y_w,y_l)$ 应用更强的更新。而第二部分 $\delta$ 是我们方法的一个独特组成部分。如图 1 所示，非偏好响应子集的 KL 散度增长率快于偏好响应子集。随着差异的增加，相应的 $\delta$ 值上升，从而放大权重因子 $\sigma (-u+\delta )$。结合后续的梯度项，我们的目标函数可以有效抑制 KL 散度差异较大的响应对之间的 KL 散度差异。我们的方法通过权重因子$\delta$和梯度项 $(-{\nabla }_{\theta }\delta )$ 的协同影响，达到了自动控制KL散度平衡的目的。
　　等式16中的损失函数梯度也由两个分量组成，${\nabla }_{\theta }u$ 和 $(-{\nabla }_{\theta }\delta )$。${\nabla }_{\theta }u$ 表示DPO中梯度的优化方向。直观上看，${\nabla }_{\theta }u$ 增加了优选补全$y_w$的似然，降低了非优选补全$y_l$的似然。而 $(-{\nabla }_{\theta }\delta )$ 倾向于缩小 $D_{SeqKL}(x,y_w;{\pi }_{ref}\Vert {\pi }_{\theta })$ 和 $D_{SeqKL}(x,y_l;{\pi }_{ref}\Vert {\pi }_{\theta })$ 之间的差距。
　　然而，如果单独考虑，损失函数中 $D_{SeqKL}(x,y_w;{\pi }_{ref}|{\pi }_{\theta })$ 的梯度在优化过程中往往会增加 $(x,y_w)$ 在 ${\pi }_{ref}$ 和 ${\pi }_{\theta }$ 之间的连续 KL 散度。这是因为损失函数中的连续前向 KL 散度是通过状态价值函数 $V_{\pi }$ 引入的，固有地在每个 token 上引入了一个期望 ${\mathbb{E}}_{z\sim {\pi }_{ref}}[log\frac{{\pi }_{\theta }(z|[x,y^{<t}])}{{\pi }_{ref}(z|[x,y^{<t}])}]$ 作为基线。这个期望的负值恰好对应于一个前向 KL 散度 $D_{KL}({\pi }_{ref}(\cdot |[x,y^{<t}])|{\pi }_{\theta }(\cdot |[x,y^{<t}]))$，它可以用来约束 KL 散度的不均衡增长。对于提示 $x$ 和首选响应 $y_w$，在每个 token 上，等式 16 中的损失函数倾向于增加 $log\frac{\pi (y_w^t|[x,y_w^{<t}])}{{\pi }_{ref}(y_w^t|[x,y_w^{<t}])}$ 的似然，同时降低期望，扩大指定项 $y_w^t$ 与基线之间的差距以加快训练。降低期望的影响是每个 token 的前向 KL 散度 $D_{KL}({\pi }_{ref}(\cdot |[x,y_w^{<t}])|{\pi }_{\theta }(\cdot |[x,y_w^{<t}]))$ 增加，从而导致 $D_{SeqKL}(x,y_w;{\pi }_{ref}|{\pi }_{\theta })$ 增加。由于我们的目标不是加快训练速度而是确保训练稳定性，我们通过停止 $D_{SeqKL}(x,y_w;{\pi }_{ref}|{\pi }_{\theta })$ 的梯度传播并将其视为 $D_{SeqKL}(x,y_l;{\pi }_{ref}|{\pi }_{\theta })$ 对齐的基线项来修改损失函数。
　　与 $D_{SeqKL}(x,y_w;{\pi }_{ref}|{\pi }_{\theta })$ 不同，$D_{SeqKL}(x,y_l;{\pi }_{ref}|{\pi }_{\theta })$ 的梯度倾向于减少 $(x,y_l)$ 处 ${\pi }_{ref}$ 和 ${\pi }_{\theta }$ 之间的连续 KL 散度。对于提示 $x$ 和被拒绝的响应 $y_l$，等式 16 中的损失函数倾向于降低每个 token 处 $log\frac{\pi (y_l^t|[x,y_l^{<t}])}{{\pi }_{ref}(y_l^t|[x,y_l^{<t}])}$ 的似然，同时增加期望 $E_{z\sim {\pi }_{ref}}[log\frac{{\pi }_{\theta }(z[x,y_l^{<t}])}{{\pi }_{ref}(z|[x,y_l^{<t}])}$。期望的增加意味着该 token 处的前向 KL 散度更小，从而起到限制连续前向 KL 散度增长率的作用。因此，对于这一项，我们选择保留其梯度更新。
　　综上所述，我们只在 $(-{\nabla }_{\theta }\delta )$ 中传播 $D_{SeqKL}(x,y_l;{\pi }_{ref}|{\pi }_{\theta })$ 的梯度，当第二部分权重因子$\delta$变大时，对 $D_{SeqKL}(x,y_l;{\pi }_{ref}||{\pi }_{\theta })$ 施加更强的抑制，以控制KL散度的平衡。
　　此外，为了在 TDPO 中实现对齐性能和生成多样性之间的更好平衡，我们在损失函数中引入了一个附加参数 $\alpha$，通过调整 $\alpha$ 的大小可以控制 $D_{SeqKL}(x,y_w;{\pi }_{ref}||{\pi }_{\theta })$ 和 $D_{SeqKL}(x,y_l;{\pi }_{ref}||{\pi }_{\theta })$ 之间的偏差。

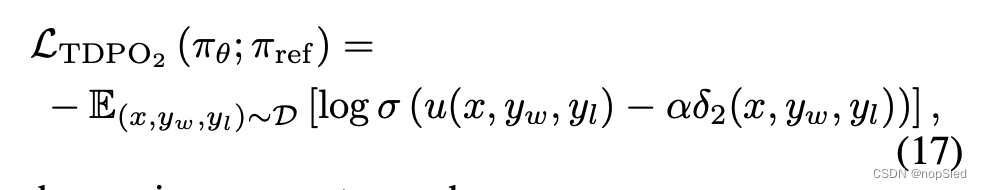
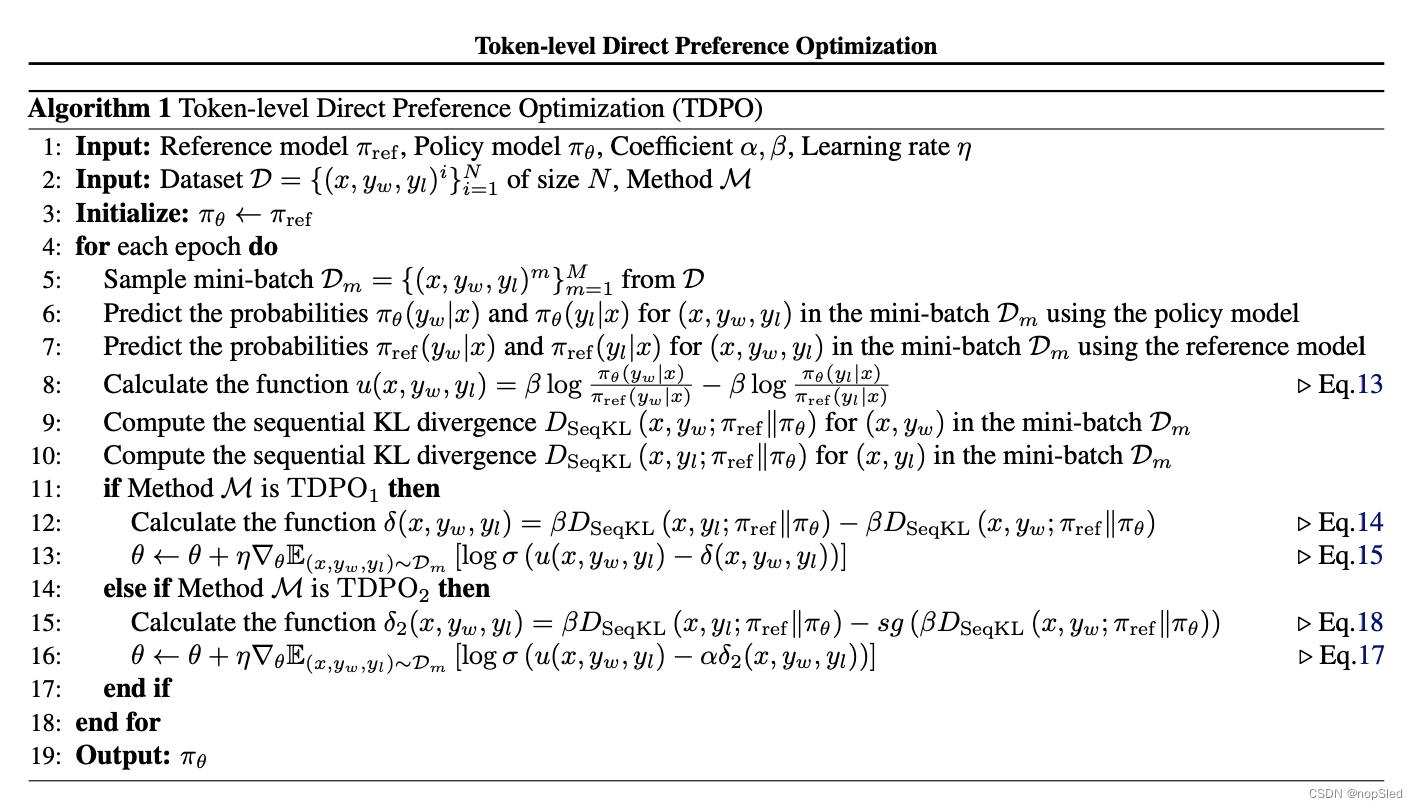
　　利用参数 $\beta$ 来调节语言模型与基础参考模型的偏差，以及利用 $\alpha$ 来控制语言模型中顺序 KL 散度的平衡，我们的方法实现了与人类偏好的出色一致性，同时有效地保留了模型生成的多样性。我们在算法 1 中提供了伪代码，并在附录 B 中提供了 TDPO 损失的 Pytorch 实现版本。

5.Experiments