周期为2pi的函数展开为傅里叶级数
周期为2pi的函数
周期
T
=
2
π
f
(
x
)
=
f
(
x
+
2
π
)
T=2\pi \quad f(x)=f(x+2\pi)
T=2πf(x)=f(x+2π)

把三角函数转化为无数三角函数的加和
f
(
x
)
=
∑
n
=
0
∞
a
n
c
o
s
n
x
+
∑
n
=
0
∞
b
n
s
i
n
x
=
a
0
c
o
s
0
x
+
∑
n
=
1
∞
a
n
c
o
s
n
x
+
b
0
s
i
n
0
x
+
∑
n
=
1
∞
b
n
s
i
n
x
=
a
0
+
∑
n
=
1
∞
a
n
c
o
s
n
x
+
∑
n
=
1
∞
b
n
s
i
n
x
\begin{aligned} f(x) &=\sum_{n=0}^{\infty}a_n cos nx+ \sum_{n=0}^{\infty}b_n sinx \\ &= a_0 cos0x + \sum_{n=1}^{\infty}a_n cos nx + b_0 sin0x + \sum_{n=1}^{\infty}b_n sinx \\ &=a_0 + \sum_{n=1}^{\infty}a_n cos nx + \sum_{n=1}^{\infty}b_n sinx \\ \end{aligned}
f(x)=n=0∑∞ancosnx+n=0∑∞bnsinx=a0cos0x+n=1∑∞ancosnx+b0sin0x+n=1∑∞bnsinx=a0+n=1∑∞ancosnx+n=1∑∞bnsinx
而有些教科书上的定义为:
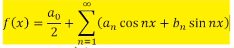
求a0
∫
−
π
π
f
(
x
)
d
x
=
∫
−
π
π
a
0
d
x
+
∫
−
π
π
∑
n
=
1
∞
a
n
c
o
s
n
x
d
x
+
∫
−
π
π
∑
n
=
1
∞
b
n
s
i
n
x
d
x
=
a
0
∫
−
π
π
d
x
=
a
0
x
∣
−
π
π
=
2
π
a
0
\begin{aligned} \int_{-\pi}^{\pi}f(x)dx &= \int_{-\pi}^{\pi} a_0 dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty}a_n cos nx dx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty}b_n sinx dx \\ &= a_0 \int_{-\pi}^{\pi} dx = a_0 x \mid_{-\pi}^{\pi} = 2 \pi a_0 \end{aligned}
∫−ππf(x)dx=∫−ππa0dx+∫−ππn=1∑∞ancosnxdx+∫−ππn=1∑∞bnsinxdx=a0∫−ππdx=a0x∣−ππ=2πa0
所以:
a
0
=
1
2
π
∫
−
π
π
f
(
x
)
d
x
a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx
a0=2π1∫−ππf(x)dx
可能是为了抹去分母上的2,许多教科书上把公式定义为
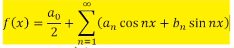
此时:
a
0
=
1
π
∫
−
π
π
f
(
x
)
d
x
a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)dx
a0=π1∫−ππf(x)dx
求an
等式两边乘以
c
o
s
m
x
cosmx
cosmx,求积分
∫
−
π
π
f
(
x
)
c
o
s
m
x
d
x
=
∫
−
π
π
a
0
2
c
o
s
m
x
d
x
+
∫
−
π
π
∑
n
=
1
∞
a
n
c
o
s
n
x
c
o
s
m
x
d
x
+
∫
−
π
π
∑
n
=
1
∞
b
n
s
i
n
n
x
c
o
s
m
x
d
x
\begin{aligned} \int_{-\pi}^{\pi}f(x)cosmxdx &= \int_{-\pi}^{\pi} \frac{a_0}{2} cosmxdx + \int_{-\pi}^{\pi} \sum_{n=1}^{\infty}a_n\;cosnxcosmxdx+ \int_{-\pi}^{\pi} \sum_{n=1}^{\infty}b_nsinnxcosmxdx \end{aligned}
∫−ππf(x)cosmxdx=∫−ππ2a0cosmxdx+∫−ππn=1∑∞ancosnxcosmxdx+∫−ππn=1∑∞bnsinnxcosmxdx
等式的右边只剩下
n
=
m
n = m
n=m 的情况下不等于0
∫
−
π
π
f
(
x
)
c
o
s
m
x
d
x
=
∫
−
π
π
f
(
x
)
c
o
s
n
x
d
x
=
∫
−
π
π
∑
n
=
1
∞
a
n
c
o
s
n
x
c
o
s
n
x
d
x
=
a
n
∫
−
π
π
∑
n
=
1
∞
c
o
s
n
x
2
d
x
=
a
n
π
\begin{aligned} \int_{-\pi}^{\pi}f(x)cosmxdx &= \int_{-\pi}^{\pi}f(x)cosnxdx \\ &= \int_{-\pi}^{\pi} \sum_{n=1}^{\infty}a_n\;cosnxcosnxdx \\ &=a_n\int_{-\pi}^{\pi} \sum_{n=1}^{\infty}\;cosnx^2dx \\ &=a_n \pi \end{aligned}
∫−ππf(x)cosmxdx=∫−ππf(x)cosnxdx=∫−ππn=1∑∞ancosnxcosnxdx=an∫−ππn=1∑∞cosnx2dx=anπ
所以: a n = 1 π ∫ − π π f ( x ) c o s n x d x a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)cosnxdx an=π1∫−ππf(x)cosnxdx
求bn
等式两边乘以 s i n m x sinmx sinmx,求积分
所以: b n = 1 π ∫ − π π f ( x ) s i n n x d x b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)sinnxdx bn=π1∫−ππf(x)sinnxdx
结论
周期为 2 π 2\pi 2π函数的傅里叶展开为:
f ( x ) = f ( x + 2 π ) T = 2 π f(x)=f(x+2\pi) \quad T=2\pi f(x)=f(x+2π)T=2π
f ( x ) = a 0 2 + ∑ n = 1 ∞ a n c o s n x + ∑ n = 1 ∞ b n s i n x f(x) =\frac{a_0}{2} + \sum_{n=1}^{\infty}a_n cos nx + \sum_{n=1}^{\infty}b_n sinx f(x)=2a0+∑n=1∞ancosnx+∑n=1∞bnsinx
a 0 = 1 2 π ∫ − π π f ( x ) d x a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx a0=2π1∫−ππf(x)dx
a n = 1 π ∫ − π π f ( x ) c o s n x d x a_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)cosnxdx an=π1∫−ππf(x)cosnxdx
b n = 1 π ∫ − π π f ( x ) s i n n x d x b_n = \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)sinnxdx bn=π1∫−ππf(x)sinnxdx
原视频:
https://www.bilibili.com/video/av34556069/?spm_id_from=333.788.videocard.0





















 2230
2230











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








