Robust Differential Game Guidance Laws Design for Uncertain Interceptor-Target Engagement via ADP

原文：https://download.csdn.net/download/qq_29675093/10969822

南京航空航天大学孙景亮的论文，二人零和博弈框架下研究导弹拦截机动目标，使用的方法是自适应动态规划，从理念上跟利用critic网络进行强化学习很接近的，但是由于模型已知，使用残差可以直接根据模型调整critic网络的权值，而控制量也是critic网络权值的函数。

本文中的critic网络其实不是我们一般理解的神经网络，实质只是高阶线性近似函数，网络权值也只是拟合系数。

看起来作者的理论功底非常扎实，能够把交战闭环系统和评价近似函数的稳定性都给出理论证明。在一定程度上，可以说作者完整解决了整个问题。当然如果能直接处理三维空间下的问题，并能够对不同的目标、拦截导弹参数和初始状态设定给出更充分的仿真分析就更好了。另外权值初值，学习率，R1，R2等这些参数的设定若是能给出一些设定准则也是好的。还有就是没有考虑最大角加速度（过载）约束，这是不现实的，也无法考虑不能拦截的情况。

成本函数是由状态评价、双方各自的控制机动成本加和给出，适用范围也有限，并没有利用好强化学习的优势。

摘要：

在本文中，拦截机动目标的问题被设定为受匹配不确定性影响的二人零和微分博弈框架。
①通过引入反映不确定性的适当的成本函数，鲁棒控制转化为二人零和微分博弈控制问题，从而确保对所匹配的不确定性的补偿。
②另外，通过构造评价神经网络（NN）来求解相应的Hamilton-Jacobi-Isaacs（HJI）方程。
③利用Lyapunov方法证明了闭环系统和评价NN权值估计误差的统一极限有界性（UUB）。【这一部分我没翻译，看不太懂】
④最后，通过使用非线性二维运动学，假设拦截器和目标的一阶动力学，验证了所提出的鲁棒制导律的有效性。

1.简介

在现代战争中，制导导弹的主要目标是成功拦截目标，同时优化能量使用以增加射程。最近，为了提高导航性能，已经开发出了繁荣的导弹制导技术的变体，例如比例导航制导（PNG）（Ratnoo＆Ghose，2008），增强比例导航制导（APNG）（Ghosh，Ghose，＆Raha，2014），滑模控制（SMC）制导（Kumar，Rao，＆Ghose，2012），线性二次微分对策（LQDG）制导（Shaferman＆Shima，2008）等。在这些技术中，PNG是最受欢迎的，并且在实际的导弹拦截活动中广泛使用。然而，在存在引导参数的不确定性和诸如目标机动的外部干扰的情况下，PNG不能很好地执行。 APNG的开发是基于拦截器已知目标的加速度。然而，任何可能采用反馈形式的策略的智能目标都会独立选择其策略，很难预测其未来的战略过程。微分博弈，特别是追逃博弈，提供了一个框架，在这个框架上需要分析两个独立的自私对手之间的对抗情况（Rajarshi＆Debasish，2015）。此后，LQDG成功应用于目标拦截问题，基于微分博弈制导的状态依赖Riccati方程（SDRE）（Bardhan＆Ghose，2012）也成功应用于目标拦截问题。但是，基于LQDG和SDRE的制导律都要求来自碰撞过程周围的线性化几何，需要估计剩余时间或不考虑内部或外部干扰的鲁棒性。 SMC理论提供了一种可以处理系统状态非线性，大型建模误差和不确定性的鲁棒方法。基于SMC的制导方法在过去几年进行了研究（Kumar等，2012; Kumar，Rao，＆Ghose，2014），然而其中大多数制导律则是不连续的，可能需要高频控制并可能导致在实施这些制导律时震颤。

为了设计一个关于拦截器 - 目标交战动态不确定性的鲁棒的制导律，并放松对目标机动信息的需求， $H_\infty$ 制导律（Yang＆Chen，1998）和SDRE制导律（ Bardhan＆Ghose，2015; Rajarshi＆Debasish，2015）通过求解相应的HJI方程，提出了非线性运动学。然而，通过非线性微分博弈系统的分析方法找到其纳什解通常是难以处理或不可能的，这限制了制导方法的应用。求解方法通常是离线的。

自适应动态规划（ADP）作为一种有效的智能控制方法，在寻求最优控制和微分博弈解中发挥了重要作用（Zhang，Zhang，Luo，Yang，2013）。强化学习（RL）作为ADP的同义词，已被广泛用于应对非线性最优控制和微分对策问题。一般结构，名为actor-critic体系结构，用于实现ADP / RL，其中critic是近似成本函数的网络，而actor是另一个近似于控制策略的网络。近年来，通过使用ADP / RL技术进行了各种相关工作，例如稳定控制问题（Kyriakos G. Vamvoudakis＆Lewis，2010; Kyriakos G Vamvoudakis，Vrabie，＆Lewis，2011; Vrabie＆Lewis，2009），跟踪控制问题（Gao＆Jiang，2015; Kamalapurkar，Dinh，Bhasin，＆Dixon，2015; Y.-J.Liu＆Tong，2015），输出反馈控制问题（Zhu，Modares，Peen，Lewis，＆Baozeng， 2015），约束输入控制问题（D. Liu，Yang，Wang，＆Wei，2015; Xiong，Derong，＆Yuzhu，2013）， $H_\infty$ 控制问题（Modares，Lewis，＆Sistani，2014），微分博弈问题（K. Vamvoudakis，Vrabie，＆Lewis，2012; Yasini，Sistani，＆Karimpour，2015），鲁棒控制问题（Fu，Fu，＆Chai，2015; Wang，Liu，Li，＆Ma，2014; Zhang＆Zhang， 2014）等。

在实际的拦截器 - 目标交战中，外部干扰和建模误差会严重降低闭环系统性能。一种可能的解决方案是采用鲁棒的策略来改善制导性能并减少无功脱靶量（ZEMD）。遗憾的是，基于ADP的不确定非线性系统的鲁棒最优控制结果很少，更不用说拦截器 - 目标交战微分博弈问题了。在（Fu et al，2015）中，作者通过扩展（Zhang＆Zhang，2014）结果开发了一种具有匹配不确定性的线性系统的鲁棒微分博弈控制器。虽然所提出的鲁棒控制器是在未知系统的情况下实现的，但是需要初始稳定控制，这是非线性拦截器 - 目标交战动力学的相当严格的限制条件。

在本文中，通过在适当的成本函数下修改名义上的系统的Nash解，建立了一类具有不确定性的非线性系统的鲁棒微分博弈控制方法（Wang et al，2014）。不受维数灾难影响的ADP技术被用于通过构建评价网络来求解相应的HJI方程。此外，受到（Dierks＆Jagannathan，2010; D. Liu等人，2015; Wang等人，2014）的工作的启发，引入了额外的稳定量以确保系统状态在在线学习过程中保持在有限范围内。利用Lyapunov直接法，将闭环微分博弈系统和评价NN权重估计误差证明为UUB，并给出了系统状态的最终界限。
本文的主要贡献包括：
1）利用基于ADP / RL的微分博弈方法研究拦截器 - 目标交战的鲁棒制导律，以提高制导性能。

2）与（K.Vamvoudakis等，2012; Yasini等，2015）相比，本文提出的算法的一个明显优势是构造了一个更简单的算法架构，即只采用一个评价网络而不是两个或三个网络来实现算法，这降低了计算的复杂性。
本文的其余部分安排如下。在第2节中，我们提出了一般问题陈述和预备。在第3节中设计了不确定非线性二人零和微分博弈的鲁棒控制器，并给出了稳定性证明。在第4节中开发了然后基于ADP的鲁棒微分博弈控制器，并给出了稳定性证明。在第5节中，介绍了用于制导律推导和模拟的拦截器 - 目标交战的数学模型。最后，第6节证明和分析了制导律的执行情况，随后是第7节的结论。
在本文中， $R^n$ 和 $R^{n\times m}$ 分别表示n维欧氏空间和所有 $n \times m$ 个实矩阵的集合; $\Omega$ 是 $R^n$ 的紧凑集;当 $\xi$ 是向量时， $\left \| \xi \right \|$ 表示 $\xi$ 的欧几里德范数;当A是矩阵时， $\left \| A \right \|$ 表示A的二范数;矩阵M的转置由 $M ^T$ 表示; $P>0$ 表示矩阵P是正定的; x * 表示变量x的最优值;

2.问题陈述和预备

在本节中，我们研究了连续时间不确定非线性二人零和微分博弈

（1）
其中 $\dot x(t) \in R^n$ 是状态向量， $\bar{u}(t)\in R^k$ 和 $\bar{v}(t)\in R^m$ 是两个参与者的两个控制输入向量；在 $f(0)=0$ 的条件下 $f(\cdot )$ ， $g(\cdot)$ 和 $k(\cdot)$ 是可微的； $\bar d(x(t))$ ， $\bar b(x(t))$ 对于双方是未知非线性匹配不确定性的。假设f（x）是局部Lipschitz连续的，使得系统（1）是可控的。设 $x(0)=x_0$ 为初始状态。假设 $\bar{d}(0)=0$ ， $\bar{b}(0)=0$ 使得x=0是系统（1）的平衡点。
标称系统[即，没有不确定性的系统（1）]描述为

（2）
为方便起见，将x（t）表示为x，在一些后续公式中省略了时间变量t。
对于系统（1），为了处理匹配的不确定性，应该找到控制对，使得闭环系统对于所有不确定性是全局渐近稳定的。为此，在本文中，我们将此问题转换为找到具有适当成本函数的相应名义零和微分博弈的Nash解。
设 $R_1\in R^{k\times k}$ ， $R_2\in R^{m\times m}$ 是两个对称正定矩阵。然后，我们假设，其中都由已知函数界定，

对于标称系统（2），考虑到系统（1）对应的不确定性，目标是设计一个最小化无限时间成本函数的控制输入 $u(t)$ 和另一个最大化无限时间成本函数的控制输入 $v(t)$ ，成本函数由下式给出

（3）
，Q1是对称正定矩阵，正标量c>1是必不可少的，它将是一个影响本文系统收敛的关键设计参数。
备注1：包含若干部分的量恰当地反映了不确定性和正则性。显然，它是正的。根据Nash-Pontryagin Minimax原理，设计的控制器不仅可以最小化正则误差，还可以最小化不确定性，这表明了对不确定性的鲁棒性。（3）中描述的成本函数给出了关于不含不确定性的零和微分博弈问题的修改版本。

本文感兴趣的问题是找到最优控制对 $u(t)$ 和 $v(t)$ ，使得动态系统（2）从给定的初始状态x0转移到任意最终状态，并且使得成本函数（3）是相对于 $u(t)$ 最小化并且相对于 $v(t)$ 最大化。

定义系统（2）的哈密顿函数如下：

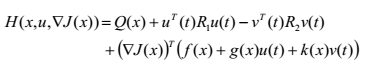（4）

J（0）=0，符号是梯度运算的符号，例如。

在Nash-Pontryagin Minimax原理中，我们已经表达了哈密顿函数 $H(\cdot)$ 相对于控制对（u（t），v（t））具有纳什均衡或特殊类型的鞍点的必要条件。两个不等式在最优控制对（u *（t），v *（t））处满足

（5）
根据Hamilton-Jacobi-Isaacs（HJI）理论，最优成本函数J *（x）由下式给出：

（6）
并且J *（0）=0。然后通过求解HJI方程可以得到最优代价函数J *（x）

（7）

假设（7）的鞍点存在并且是唯一的。然后，最佳控制对是

（8）

根据（4）和（8），HJI方程（7）为

（9）

J *（0）=0。

3 不确定非线性二人零和微分对策的鲁棒控制器设计

在本节中，受到（Wang et al，2014）的工作的启发，考虑具有不确定性的系统（1），为了补偿匹配的不确定性，我们修改了系统（2）的最优控制对（8）如下：

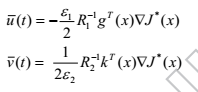（10）
其中是反馈增益。
现在，我们提出以下引理来表明修改后的控制对具有无限的增益余量。

引理1：对于标称系统（2），（10）中给出的修改控制对确保闭环系统渐近稳定，只要反馈增益

满足。

证明：我们表示最优成本函数J *（x）是Lyapunov函数。在（3）的视图中，我们可以很容易地发现J *（x）是正定的。考虑到（9）和（10），J *（x）沿闭环系统轨迹的导数是

（11）

因此， J * (x) < 0，只要， $x\neq 0$ 。那么满足Lyapunov局部稳定定理的条件。

定理1：对于系统（1），总是存在两个反馈增益满足其中c由（3）给出，使得（10）中开发的修改的控制对确保闭环系统渐近稳定。

根据定理1，修改的控制对u（t）和v（t）实现了受不确定性影响的系统（1）的鲁棒性。接下来，我们将证明修改的控制对具有的最优性。
对于系统（1），我们定义以下成本函数

其中

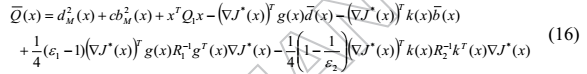
定理2：考虑具有无限时间代价函数（15）的系统（1）。总是存在两个反馈增益，使得由（10）获得的修改的控制对是微分博弈问题的渐近稳定的Nash解。

为了应用评价网络来近似纳什解决方案并保证其稳定性，提出了以下常见假设（Dierks＆Jagannathan，2010）。

假设1：设J s（x）是满足的连续可微的Lyapunov函数候选

假设存在正定矩阵 $\Lambda (x)$ ，使得以下关系成立：

设 $\lambda_{min}$ 和 $\lambda_{max}$ 是矩阵 $\Lambda (x)$ 的最小和最大特征值，则不等式成立。

4. ADP 的Critic网络及稳定性分析

根据Weierstrass高阶近似定理（Abu-Khalaf＆Lewis，2005），最优代价函数可以通过神经网络近似，

其中 $w_c \in R^N$ 是理想权重， $\sigma (x) \in R^N$ 称为神经网络激活函数向量，N是隐藏层中神经元的数量， $\varepsilon _c(x)$ 是神经网络近似误差。然后它相对于x的导数

将（25）代入最优控制对（8）得到

哈密顿函数（4）变为

由于为（27）提供最佳近似解的神经网络的理想权重是未知的，因此评价神经网络的输出是

其中 $\hat{w}_c$ 是 $w_c$ 的当前估计值。
同样，我们有

根据（8）和（29），近似的控制对可以给出为

将（26）代入哈密顿函数（4）得到

由函数逼近误差引起的残差是

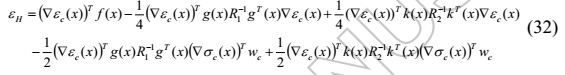
使用近似控制对和估计的权重向量，可以推导出近似哈密顿函数

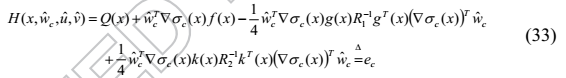
$e_c$ 是一个残差方程误差。（译者注：根据上下文，上式 $e_c$ 有误， $e_c\doteq H(x,\hat{w}_c,\hat{u},\hat{v})-H(x,\hat u,\hat v)$ ）
定义评价权重估计误差，然后，基于（31）和（33），残差方程误差可以修改为

给定任何反馈控制对u（t）和v（t），需要设计 $\hat{w}_c$ 以最小化平方残差误差

。

备注2：观察近似哈密顿函数（33），估计的权重 $\hat{w}_c$ 应设计为最小化（33）。但是，它不能确保在线学习过程中系统（2）的稳定性。因此，在考虑系统的稳定性（2）时，应考虑改进的调整法以最小化（33）。

选择评价估计权值的调整律作为归一化梯度下降算法，并引入附加项以确保系统状态的有界性，即

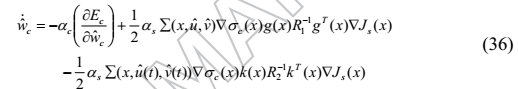
其中 $\alpha_c >0$ 是评价网络的学习率， $\alpha_s >0$ 是附加项的调节参数。 $J_s(x)$ 是假设1中给出的Lyapunov函数候选，而是附加稳定项，定义为

应该提到的是，调整律（36）中的第一项旨在最小化（35），（36）的其余部分确保系统状态保持有界，而神经网络逼近器学习最优成本函数。

推导附加项的过程如下：

用控制对（8）表示系统（2）的Lyapunov函数候选的导数

如果闭环系统不稳定，我们可以得到F> 0。为了通过使用梯度下降法保持闭环系统稳定，即F <0，我们得到了

因此，附加项（39）对于所提出的调整法是必要的，以确保在线学习过程期间闭环系统的稳定性。
定义（37）表明，当非线性系统稳定时，（36）的第二项和第三项被删除。相反，当系统表现出不稳定的迹象时，（36）的第二和第三项被激活用于学习过程（Dierks＆Jagannathan，2010）。

为了证明上述调整律的稳定性，应给出评价权重估计误差的动态。考虑和

获得了误差动态

假设2：
不失一般性，
（1）内部动力学f（x）是Lipschitz连续的，输入动力学g（x）和k（x）是有界的。即，存在常数，使得
（2）理想的神经网络权重 $w_c$ 受已知常数 $w_M$ 的限制，即
（3）神经网络近似误差 $\varepsilon _c(x)$ 及其梯度 $\triangledown \varepsilon _c(x)$ 是有界的，使得。
（4）神经网络激活函数 $\sigma _c(x)$ 及其梯度 $\triangledown \sigma _c(x)$ 也是有界的，使得。

定义1：（Kyriakos G Vamvoudakis等，2011）（UUB）如果存在紧集 $S\subset R^n$ ，对于所有，存在一个约束M和一个时间，使得，则时间信号 $\zeta (t)$ 被称为均匀最终有界（UUB）。
定理3：对于系统（2），控制对 $\hat {u}(t),\hat{v}(t)$ 由（30）提供，评价神经网络的调整法由（36）提供。则评价网络的权值估计误差为UUB。（证明略）

接下来，我们推出了一个定理，严格地表明闭环系统在评价网络学习过程中在统一的最终有界性意义上是稳定的。
定理4：考虑系统（2）和相关的HJI方程（9），控制对 $\hat {u}(t),\hat{v}(t)$ 由（30）提供，评价神经网络的调整律由（36）提供。则闭环系统保证是UUB，在（70）中具有最终界限 $\Omega_x$ 。

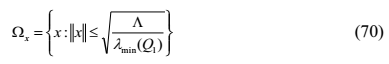
根据标准Lyapunov扩展定理（Lewis等，1998），这验证了闭环系统的轨迹是UUB。也就是说，在评价网络学习过程中，闭环系统在统一的最终有界性意义上是稳定的。

5. 应用

在本节中，我们首先构建了拦截器 - 目标交战场景的数学模型。然后，描述制导律以确保成功捕获。最后，制定了不确定非线性微分对策框架，以适应拦截器 - 目标交战问题第Ⅲ节中提出的制导律。

A.交战情景

考虑拦截器和目标之间的平面交战场景，如图1所示， $V_I$ 和 $V_T$ 是拦截器和目标的速度矢量，它们的飞行路径角（FPA）是 $\alpha$ 和 $\beta$ ，u和v是垂直于拦截器和目标速度的控制矢量。假设拦截器和目标具有恒定的速度。视线（LOS）角由 $\theta$ 给定，LOS角速度为 $\dot{\theta}$ ,由 $\sigma$ 指代。目标与拦截器之间沿LOS的相对距离由r给出。可变量的初始值将用下标0表示。拦截器 - 目标交战系统的运动学由以下等式给出：

B.制导原则

为了确保捕获，拦截器必须选择其策略u以最小化零功脱靶量，而智能目标将选择其策略v以最大化终端脱靶量。因此，该问题以拦截器试图最小化终端脱靶量，而目标试图使其最大化的形式提出。因此，零功脱靶量（ZEMD）定义如下（Bardhan＆Ghose，2015）。
定义1（零功脱靶量）在时刻t的零功脱靶量被定义为，如果拦截器和目标从该瞬间开始都不机动，拦截器和目标之间的最近距离 $r_{miss}(t)$ ，值为

从方程式中的 $r_{miss}(t)$ 的表达式（75），可以看出，将 $\sigma$ 调为零意味着将 $r_{miss}(t)$ 调节为零值，而且保持 $V_r<0$ 的同时将 $\sigma$ 调节为零会导致拦截。

C.不确定的非线性微分博弈框架

根据制导律，将LOS角速率 $\sigma$ 归零将导致拦截，然后通过调整控制向量u实现 $\sigma$ 的收敛，可以得到制导律。选择系统状态为 $\sigma$ ，即 $x=\sigma$ ，在时域内微分方程（72）

注意，作为u和v分别被乘，LOS角速率 $\sigma$ 可控制所有。可以证明是不稳定的平衡。
因此，基于微分博弈的制导律适用的范围由下式给出

考虑到拦截器和目标的模型不确定性，拦截器 - 目标交战动力学被描述为

6.模拟

在本节中，将使用获得的拦截器 - 目标交战模型来研究从基于ADP / RL的微分博弈导出的制导律的性能。制导律是在假设拦截器和目标的理想自动驾驶仪的情况下推导出来的，然而，用于模拟研究的拦截器和目标是具有一阶动力学的自动驾驶仪。
拦截器的运动方程如下：

其中 $(x_I,y_I)$ 是拦截器的（x，y）坐标， $a_I$ 表示拦截器的横向加速度， $\tau_I$ 是拦截器自动驾驶仪的时间常数。
目标的运动方程如下：

其中 $(x_T,y_T)$ 是目标的（x，y）坐标， $a_T$ 表示目标的横向加速度， $\tau_T$ 是目标自动驾驶仪的时间常数。
拦截器和目标速度在交战期间被认为是恒定的，并且取为。拦截器和目标自动驾驶仪的时间常数为。
假设拦截器和目标的初始FPA角为 $\alpha_0=30^{\circ}$ 和 $\beta_0=125^{\circ}$ ，初始LOS角 $\theta_0=0^\circ$ ，拦截器和目标的初始坐标为 $(x_I,y_I)=(0,0)$ 和 $(x_T,y_T)=(2500,0)$ 。对于稳健的微分博弈制导律，常数增益为。哈密顿方程中，恒定标量c=36，加权矩阵 $Q_1=200,R_1=0.1$ 和 $R_2=0.1$ 。评价网络的初始权值是，激活函数是，学习率为，Lyapunov函数候选是。

假设这个量反映了拦截器的不确定性，而这个量反映了目标的不确定性，其中是未知参数，其中和。

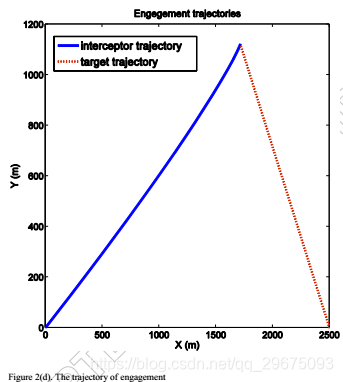
在模拟之后，状态变量 $x=\sigma$ 在大约3.4s处被调节为零，如图2（a）所示，其根据方程式（75）将ZEMD导向零。同时，图2（b）显示保持负 $V_r$ 以确保拦截器和目标之间的相对距离r（如图2（c）所示）减小。因此，脱靶量小于0.5米，并且在模型不确定性的当前图2（d）中成功实现了拦截。图3示出了拦截器和目标的相应的横向加速度曲线，其中当r急剧减小时，横向加速度朝向啮合的末端射出。此外，评价网络的权值和残差如图4所示，这表明评价网络有效地实现了ADP方法来寻找非线性二人零和微分博弈的纳什解。与现有的与ADP相关的文献不同，网络权重不会收敛到最优值，而是在交战结束时上升，因为残差错误表现不正常。

事实上，图4中网络的不稳定行为和残差与图2中的角速率和图3中的横向加速度的行为一致。在拦截前几秒钟，残差显示出一条尖锐的曲线朝向零，然后似乎快速走向负无穷大。这种行为的原因是制导律基于拦截器和目标之间的相对距离r的值。因此，预期交战结束时的这种急剧曲线，因为两个游隙的横向加速度随着相对距离r接近零而增加，导致LOS角速率的较大误差。实际上，一旦r变小，最好停止计算目标的横向加速度，并根据为r计算的最后一个值简单地计算拦截器的横向加速度。
仿真结果表明了本文提出的基于ADP的鲁棒微分博弈制导律的有效性。

7.结论

在本文中，我们通过ADP技术开发了一类新的鲁棒微分博弈方法，用于一类不确定非线性双参数零和微分博弈系统。在指定的成本函数下证明了控制对的鲁棒性和最优性。通过构建评价网络来解决相应的HJI方程。在均匀极限有界意义下，证明了评价网络的闭环系统和权值估计误差是稳定的。通过使用所提出的稳健差分博弈方法来验证其有效性和制导性能，来考虑拦截器 - 目标交战。

致谢

这项工作得到了国家自然科学基金的资助，编号为No.61473147。

References

Abu-Khalaf, M., & Lewis, F. L. (2005). Nearly optimal control laws for nonlinear systems with saturating actuators using a neural network HJB approach. Automatica, 41(5), 779-791

Bardhan, R., & Ghose, D. (2012). Intercepting maneuvering target with specified impact angle by modified SDRE technique American Control Conference (ACC), 2012 (pp. 4613-4618): IEEE.

Bardhan, R., & Ghose, D. (2015). Nonlinear Differential Games-Based Impact-Angle-Constrained Guidance Law. Journal of Guidance, Control, and Dynamics, 38(3), 384-402. doi: 10.2514/1.G000940 Dierks, T., & Jagannathan, S. (2010). Optimal control of affine nonlinear continuous-time systems American Control Conference (ACC), 2010 (pp. 1568-1573).

Fu, Y., Fu, J., & Chai, T. (2015). Robust Adaptive Dynamic Programming of Two-Player Zero-Sum Games for Continuous-Time Linear Systems. Neural Networks and Learning Systems, IEEE Transactions on, 26(12), 3314-3319. doi: 10.1109/TNNLS.2015.2461452

Gao, W., & Jiang, Z.-P. (2015). Linear optimal tracking control: an adaptive dynamic programming approach American Control Conference (ACC), 2015 (pp. 4929-4934): IEEE.

Ghosh, S., Ghose, D., & Raha, S. (2014). Capturability of Augmented Pure Proportional Navigation Guidance Against Time-Varying Target Maneuvers. Journal of Guidance, Control, and Dynamics, 37(5), 1446-1461

Kamalapurkar, R., Dinh, H., Bhasin, S., & Dixon, W. E. (2015). Approximate optimal trajectory tracking for continuous-time nonlinear systems. Automatica, 51, 40-48. doi: http://dx.doi.org/10.1016/j. automatica.2014.10.103

Kumar, S. R., Rao, S., & Ghose, D. (2012). Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints. Journal of Guidance, Control, and Dynamics, 35(4), 1230-1246

Kumar, S. R., Rao, S., & Ghose, D. (2014). Nonsingular terminal sliding mode guidance with impact angle constraints. Journal of Guidance, Control, and Dynamics, 37(4), 1114-1130

Lewis, F., Jagannathan, S., & Yesildirak, A. (1998). Neural network control of robot manipulators and non-linear systems: CRC Press.

Liu, D., Yang, X., Wang, D., & Wei, Q. (2015). Reinforcement-Learning-Based Robust Controller Design for Continuous-Time Uncertain Nonlinear Systems Subject to Input Constraints. Cybernetics, IEEE Transactions on, PP(99), 1-1. doi: 10.1109/TCYB.2015.2417170

Liu, Y.-J., & Tong, S. (2015). Adaptive NN tracking control of uncertain nonlinear discrete-time systems with nonaffine dead-zone input. Cybernetics, IEEE Transactions on, 45(3), 497-505

Modares, H., Lewis, F. L., & Sistani, M.-B. N. (2014). Online solution of nonquadratic two-player zero-sum games arising in theH ∞ control of constrained input systems. International Journal of Adaptive Control and Signal Processing, 28(3-5), 232-254. doi: 10.1002/acs.2348

Rajarshi, B., & Debasish, G. (2015). An SDRE Based Differential Game Approach for Maneuvering Target Interception AIAA Guidance, Navigation, and Control Conference: American Institute of Aeronautics and Astronautics.

Ratnoo, A., & Ghose, D. (2008). Impact angle constrained interception of stationary targets. Journal of Guidance, Control, and Dynamics, 31(6), 1817-1822

Shaferman, V., & Shima, T. (2008). Linear quadratic guidance laws for imposing a terminal intercept angle. Journal of Guidance, Control, and Dynamics, 31(5), 1400-1412

Vamvoudakis, K., Vrabie, D., & Lewis, F. (2012). Adaptive Optimal Control Algorithm for Zero-Sum Nash Games with Integral Reinforcement Learning AIAA Guidance, Navigation, and Control Conference (pp. 4773).

Vamvoudakis, K. G., & Lewis, F. L. (2010). Online actor–critic algorithm to solve the continuous-time infinite horizon optimal control problem. Automatica, 46(5), 878-888. doi: 10.1016/j.automatica.2010.02.018

Vamvoudakis, K. G., Vrabie, D., & Lewis, F. L. (2011). Online adaptive learning of optimal control solutions using integral reinforcement learning Adaptive Dynamic Programming And Reinforcement Learning (ADPRL), 2011 IEEE Symposium on (pp. 250-257): IEEE.

Vrabie, D., & Lewis, F. (2009). Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems. Neural Netw, 22(3), 237-246. doi: 10.1016/j.neunet.2009.03.008

Wang, D., Liu, D., Li, H., & Ma, H. (2014). Neural-network-based robust optimal control design for a class of uncertain nonlinear systems via adaptive dynamic programming. Information Sciences, 282(0), 167-179. doi: http://dx.doi.org/10.1016/j.ins.2014.05.050

Xiong, Y., Derong, L., & Yuzhu, H. (2013). Neural-network-based online optimal control for uncertain non-linear continuous-time systems with control constraints. Control Theory & Applications, IET, 7(17), 2037-2047. doi: 10.1049/iet-cta.2013.0472

Yang, C.-D., & Chen, H.-Y. (1998). Nonlinear H robust guidance law for homing missiles. Journal of Guidance, Control, and Dynamics, 21(6), 882-890

Yasini, S., Sistani, M. B. N., & Karimpour, A. (2015). Approximate dynamic programming for two-player zero-sum game related to H∞ control of unknown nonlinear continuous-time systems. International Journal of Control, Automation and Systems, 13(1), 99-109

Yu, J., & Zhong-Ping, J. (2014). Robust Adaptive Dynamic Programming and Feedback Stabilization of Nonlinear Systems. Neural Networks and Learning Systems, IEEE Transactions on, 25(5), 882-893. doi: 10.1109/TNNLS.2013.2294968

Zhang, H.-G., Zhang, X., Luo, Y.-H., & Yang, J. (2013). An Overview of Research on Adaptive Dynamic Programming. Acta Automatica Sinica, 39(4), 303-311. doi: 10.1016/s1874-1029(13)60031-2

Zhu, L. M., Modares, H., Peen, G. O., Lewis, F. L., & Baozeng, Y. (2015). Adaptive Suboptimal Output Feedback Control for Linear Systems Using Integral Reinforcement Learning. Control Systems Technology, IEEE Transactions on, 23(1), 264-273. doi: 10.1109/TCST.2014.2322778