1.三维装箱决策问题
三维装箱问题即研究如何用最少数量的箱子将物品装起来。其描述如下:
假设有n个物品,其长宽高信息分别为 ( l 1 , w 1 , h 1 ) (l_1,w_1,h_1) (l1,w1,h1), ( l 2 , w 2 , h 2 ) (l_2,w_2,h_2) (l2,w2,h2)… ( l n , w n , h n ) (l_n,w_n,h_n) (ln,wn,hn)。有容器,其容积分别为 V V V。用最少的箱子,将全部物体都装起来。
对于每个物品 i i i,假设其放入箱子的顺序,角度以及位置是 ( S i , R i , P i ) (S_i, R_i, P_i) (Si,Ri,Pi)。需要求解出集合{ ( S 1 , R 1 i , P 1 ) . . . . . ( S n , R n , P n ) (S_1, R_1i, P_1).....(S_n, R_n, P_n) (S1,R1i,P1).....(Sn,Rn,Pn)},使得所用容器数量最少。本质上是离散组合最优化问题。
而三维装箱决策问题描述如下:
假设有n个物品,其长宽高信息分别为 ( l 1 , w 1 , h 1 ) (l_1,w_1,h_1) (l1,w1,h1), ( l 2 , w 2 , h 2 ) (l_2,w_2,h_2) (l2,w2,h2)… ( l n , w n , h n ) (l_n,w_n,h_n) (ln,wn,hn)。有容器,其容积分别为 V V V。是否能用 m m m个容器,将全部物体都装起来。
可以看出,问题从计算最少容器数量变为能否用一定数量的容器能够装下。解决该问题,只需要解答出是,或者否即可。
2.三维装箱决策问题分析
三维装箱决策问题是NP-Complete问题。此类问题能够在多项式时间内验证答案是否准确,可是目前并没有任何算法能够在多项式时间内解得答案。意味着对于此类问题,一般只能采用诸如暴力解等时间复杂度很高的算法求解。当物品数n和容器数量k增加时,求得最优解所需时间也会急剧增长。
想要减短计算时间,可以使用启发式算法计算。启发式算法大致如下:
一个基于直观或经验构造的算法,在可接受的花费(指计算时间和空间)下给出待解决组合优化问题每一个实例的一个可行解,该可行解与最优解的偏离程度一般不能被预计。
其核心是基于直观或者经验去构造算法。对于装箱,理解为基于平时装箱的经验,优先选择某些组合,或者放弃某些组合。如装箱时,一般会把体积最大的物品放在最下面,这种经验可以帮助排除掉一些不合理的组合,提高计算速度。最后,尽管计算出的结果牺牲一定的准确性,但是可以缩短计算时间。而经验若足够合理,也能使得计算结果准确性不会过于低。
一种经典的Bin packing problem启发式算法是First-Fit (FF)算法其核心思想是按照一定顺序取物品,一旦当前物品能够找到合适的角度和位置能够放入容器中,则放进去。其思想与现实中装箱的方法一定程度上吻合。另外该算法也被验证出有不俗的性能,能够保证计算出来的结果小于最优结果的1.7倍。
本文将介绍一种基于First-Fit算法实现的的包材推荐算法。
3.算法描述
(1) 原理描述
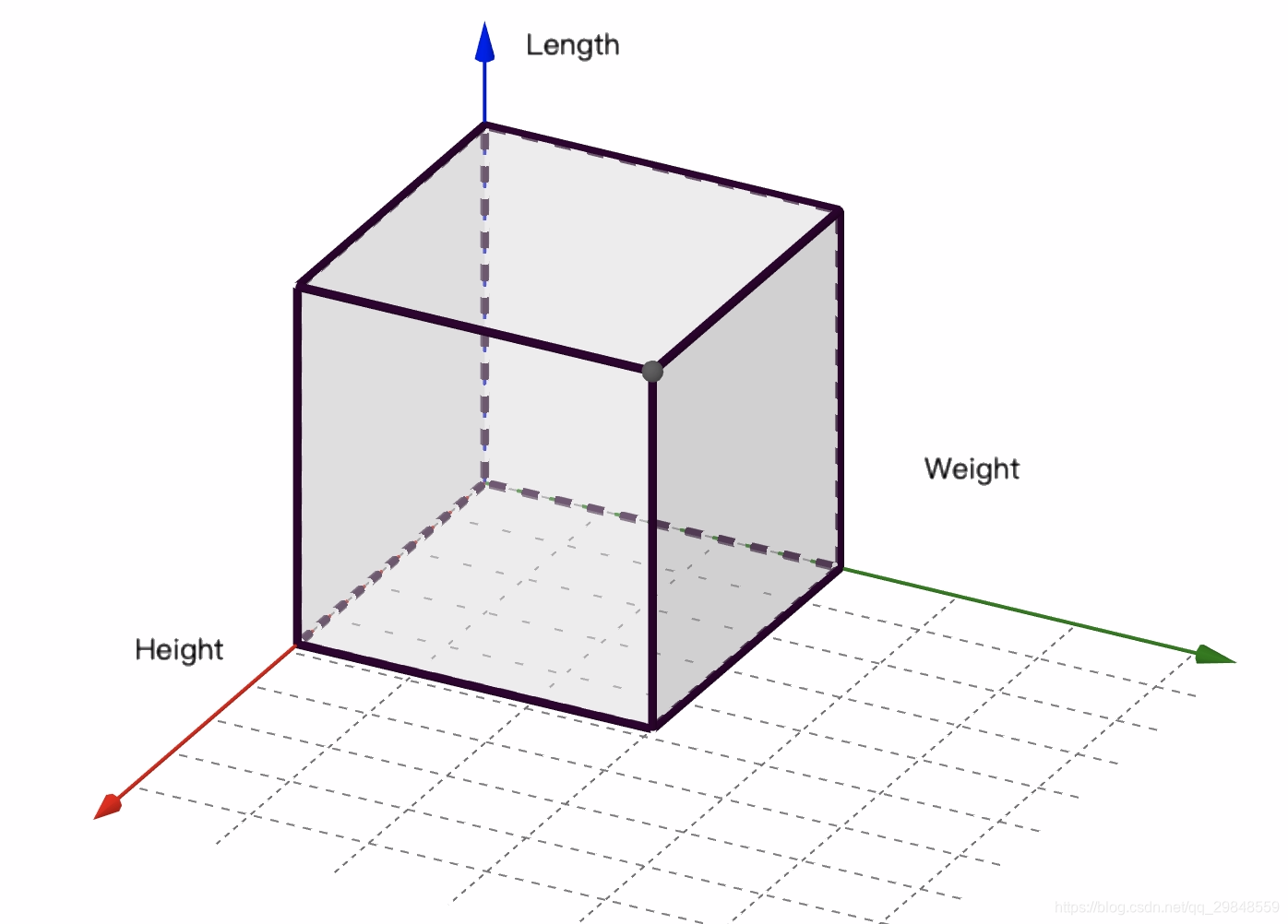
如图所示,首先建立三维坐标系,其中三个轴分别为Weight轴,Height轴和Length轴。当物体放入坐标轴时,使用其左后下顶点的坐标表示其位置。将包装箱按照各轴对应的方向置于坐标轴原点中。
接着将商品按照一定规则排序(如按体积从大到小),依次放入包装箱内。当一个商品放入箱子时,可以通过旋转物体调整方向。假设物体的尺寸为 ( w , h , l ) (w, h, l) (w,h,l),则一共有一下六种情况:
| Weight轴 | Height轴 | Length轴 |
|---|---|---|
| w w w | h h h | l l l |
| h h h | w w w | l l l |
| h h h | l l l | w w w |
| l l l | h h h | w w w |
| l l l | w w w | h h h |
| w w w | l l l | h h h |
对于第一个商品,将其放在原点处。如果当前方向无法放入,则旋转商品,直到放入为止。商品1放入后,接着放商品2。此时商品2可以选择放在商品1的前方,右方或者上方。如下图所示:
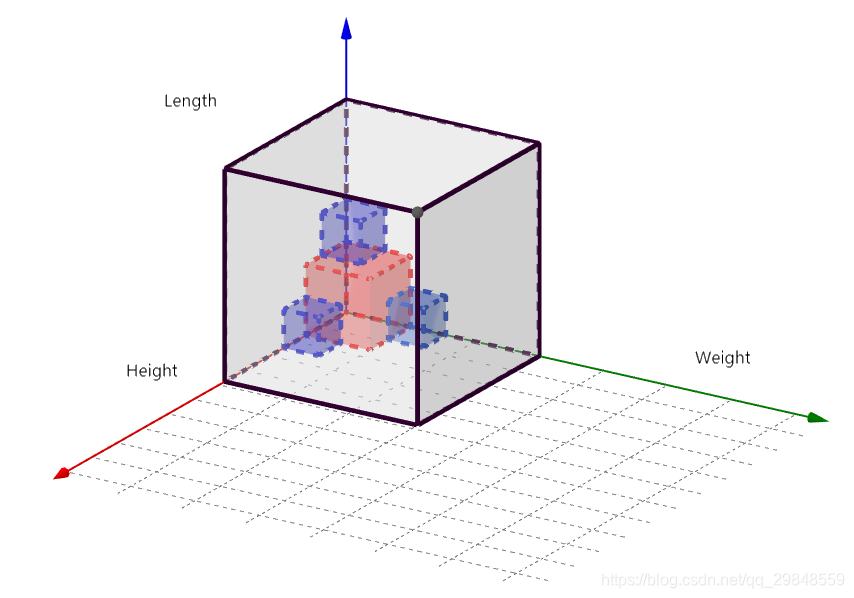
依次尝试将商品2放在这三个位置中,如果放不进,则旋转商品,一旦找到能商品放进包装箱的位置和方向,则将商品2放入。当商品3放入时,我们可以选择将商品3放入商品1的前方,右方或者上方,商品2的前方,右方或者上方。同理寻找可以将商品3放入包装箱的位置和方向,一旦找到,则将其放入。
同理对于商品n,可以选择放在商品( 1 1 1… n − 1 n-1 n−1)的前方,右方或者上方。尝试不同的位置和方向,一旦校验到商品n超出包装箱或者与包装箱中别的商品位置有重合,就通过旋转或者改变位置的方式寻找下一个存放的方式,直至商品能够放进去位置。若商品无法放入包装箱中,则认为当前包装箱无法容纳所有商品,对下一种包装箱进行计算。
即可得代码逻辑如下:
sorted_box_list <- 按照体积排序的所有包材
sorted_sku_list <- 排好序的sku
total_sku_volume <- sku总体积
rotation_list <- 六种方向
for box in sorted_box_list:
if box_volume < total_sku_volume then continue
else
fit <- false
for rotation in rotation_list:
if can_put(sku1, rotation, (0, 0, 0)) then
fit <- true
put_into_box(sku1, rotation, (0, 0, 0))
break
if fit = false then continue
for skui in sorted_sku_list[1:]:
fit <- false
find_position:
for item in box_item_list:
for position in [item_front, item_top, item_right]:
for rotation in rotation_list:
if can_put(skui, rotation, position) then
fit <- true
put_into_box(skui , rotation, position)
break find_position
if fix = false
then continue
return box
(3) 时间复杂度分析
假设一共有 k k k种包装箱,订单商品有 n n n个。对于第 i i i个商品,最多能够旋转6个方向,并且尝试放在箱子的 i − 1 i-1 i−1个商品的前、右和上3个方向。因此最多需要尝试 3 × 6 × ( i − 1 ) = 18 ( i − 1 ) 3×6×(i-1)=18(i-1) 3×6×(i−1)=18(i−1)种情况。因此可以计算得到本算法最坏情况下时间复杂度为:
T ( n ) = k × 18 × ( 1 + 2 + 3 + . . . . . . + n − 1 ) = 18 k × ( n − 1 + ( n − 1 ) ( n − 2 ) 2 ) = 18 k × n ( n − 1 ) 2 = 9 k n 2 − 9 k n = O ( k n 2 ) \begin{aligned} T(n) &=k×18×(1+2+3+......+n-1) \\ &= 18k×(n-1 + \frac{(n-1)(n-2)}{2})\\ &= 18k ×\frac{n(n-1)}{2} \\ &= 9kn^2-9kn \\ &= O(kn^2) \end{aligned} T(n)=k×18×(1+2+3+......+n−1)=18k×(n−1+2(n−1)(n−2))=18k×2n(n−1)=9kn2−9kn=O(kn2)





















 2836
2836











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








