图的深度优先遍历和计算连通分量

最新推荐文章于 2023-03-29 23:52:47 发布
VIP文章 最新推荐文章于 2023-03-29 23:52:47 发布
阅读量4.1k 收藏 25
点赞数 4
分类专栏： 图论 文章标签： 数据结构 图论
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_31965925/article/details/106295335
版权

1.深度优先遍历过程

深度优先遍历适用于有向图和无向图

复杂度：邻接表：O（V+E） 邻接矩阵:O(V^2)

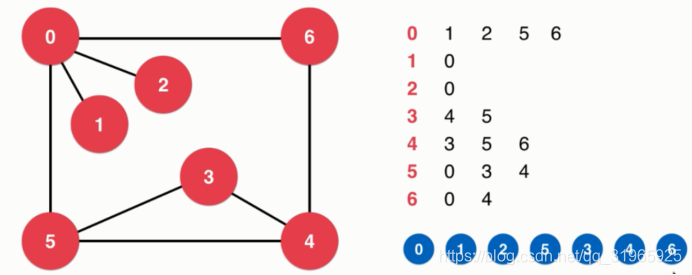
过程：

访问0: 访问0的第一个相邻结点1

访问1:1的相邻结点为0，访问过了，结点1的全部相邻结点访问完毕，退回0

接着访问0的下一个相邻结点2

访问2：2的相邻结点为0，访问过了，结点2的全部相邻结点访问完毕，退回0

接着访问0的下一个相邻结点5

访问5：5的第一个相邻结点为0，访问过了，访问下一个结点3

最低0.47元/天 解锁文章
Susceptible0506
关注
  • 4
    点赞
  • 踩
  • 25
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
图之邻接矩阵，深度遍历，广度遍历，连通分量个数
forTiffanyY的博客
11-04 4702
  1.深度遍历 DFS 类似于树的先根遍历 如图，上述图的深度遍历输出为ADCBE 给出一个图的邻接矩阵，对图进行深度优先搜索，从顶点0开始   class Graph { private: int flag[N];//状态数组 int Vexnum;//图的顶点数量 int Matrix[N][N]; //邻接矩阵 void DFS(...
图论基础（邻接矩阵，邻接表，深度优先遍历，连通分量）的实现
weixin_42226134的博客
02-14 1042
DenseGraph.h.表示邻接矩阵实现的图，一般邻接矩阵用于较为稠密的图 #ifndef DenseGraph_h #define DenseGraph_h #include <iostream> #include <vector> #include <cassert> using namespace std; //稠密图 --邻接矩阵 class De...
图的深度优先遍历和联通分量
扬俊的小屋
09-10 3511
目录 图的深度优先遍历和联通分量 深度优先遍历算法 具体的搜索思路 联通分量的计算 关键代码实现 完整代码获取 博客文章版权说明 图的深度优先遍历和联通分量 前面已经探讨了图的两种表示方法:邻接表表示法和邻接矩阵表示法。这两种表示法分别用在不同的场景上。邻接矩阵表示法主要用在稠密图中，邻...
数据结构与算法--图论之寻找连通分量、强连通分量
weixin_30628077的博客
11-11 736
数据结构与算法--图论之寻找连通分量、强连通分量 寻找无向图的连通分量 使用深度优先搜索可以很简单地找出一幅图的所有连通分量，回忆连通图的概念：如果从任意顶点都存在一条路径达到任意一个顶点，则称这幅图是连通图。而连通分量指的是一幅图中所有极大连通子图。将整幅图比喻成串了珠子的绳子的话，将任意顶点提起，连通图将是一个整体；非连通图散成若干条较小的整体，这每一条整体就是一个整幅图的一个连通分量。易知连...
2023-03-30 图的深度优先遍历的应用
lsgwr的博客
03-29 377
顶点可以分成不相交的两部分图的每条边的两个端点隶属于划分出地两部分中的一部分下面图里左边的二分图实际等效于右边的图，只是我们把连线调整了下下面是二分图的定义记录更多信息递归函数dfs()返回值联通分量ccid无路径问题(单源路径)pre有，是否遍历到了target点环检测hasCycle有，是否找到环二分图检测有，是否是二分图。
Python：利用邻接矩阵判断有向图的连通性
weixin_52365731的博客
05-20 9535
Python求解：利用邻接矩阵判断有向图的连通性 WoW，让我们先来看看我们要解决的小问题: 将任意一个有向图G采用矩阵输入，图形化输出图G，利用可达矩阵判定图G是否连通： （PS：判断图的连通性至少可以有[1].并查集 [2].DFS [3].BFS 三种方法，关于其他求解方法，详见：https://blog.csdn.net/weixin_44646116/article/details/95523884） 当然，今天我们...
学习笔记-数据结构-图的基础知识及邻接矩阵和邻接表的实现（Python）
热门推荐
Bebr的博客
06-11 1万+
一、基本概念图是一个二元组G=(V,E）。V是非空有穷的顶点集合。E是图G中边的集合。有向图：图中的每条边都有方向（即带有箭头）。无向图：图中的每条边都没有方向。有向边：用尖括号来表示为&lt;a,b&gt;。a是始点，b是终点。也被称为弧，a是弧尾，b是弧头。无向边：用圆括号表示为(a,b)。完全图：任意两个顶点之间都有边的图（有向图或无向图）。            n个顶点的无向完全图有n*...
图神经网络基础 Graph 图以及python实现
刘文凯的博客
02-22 2351
本文将介绍图的基本知识、无向图、有向图、邻接矩阵 python实现：度、连通分量、强连通图、弱连通图、图直径、度中心性、特征向量中心性、中介中心性、连接中心性等基本概念。
Python使用邻接矩阵实现图及Dijkstra算法
Joker_Lord的博客
12-05 3195
Python使用邻接矩阵实现图及Dijkstra算法 # 邻接矩阵实现无向图 Dijkstra算法 inf = float("inf") class Graph(): def __init__(self, n): self.vertexn = n self.gType = 0 self.vertexes = [inf]*n ...
Java编程实现深度优先遍历与连通分量代码示例
08-28
主要介绍了Java编程实现深度优先遍历与连通分量代码示例，
图的遍历——计算连通分量个数
05-11
要求采用邻接矩阵作为无向图的存储结构，邻接表作为有向图的存储结构，完成无向图和有向图的建立，并对建立好的图进行深度和广度优先遍历。具体实现要求： 1. 通过键盘输入图的顶点和边信息，分别构造一个无向图的...
图的遍历和生成树求解实现.cpp
01-28
功能描述：实现图的深度、广度优先遍历及两种算法下的生成树。 设计要求： 1)先任意创建一个图； 2)对图进行DFS,BFS的递归和非递归算法的实现； 3)最小生成树（两个算法）的实现，求连通分量的实现； 4)设计...
强连通分量（Strongly Connected Components）查找 原理熟悉，深度搜索，小白入手无压力
最新发布
12-13
findSCCs()函数使用深度优先搜索和Tarjan算法来进行递归遍历，并在找到一个强连通分量时将其添加到结果中。 这段代码中使用的示例图包含8个节点。你可以根据自己的需求修改图的大小和结构部分。运行该代码，你将会...
（有向）图的深度优先遍历算法模板算法(java源码)
01-21
* （有向）图的深度优先遍历算法模板 */ package dsa; public abstract class DFS extends GraphTraverse { //变量 protected static int clock = 0;//遍历过程中使用的计时钟 //构造方法 public DFS(Graph g...
图的广度优先遍历和最短路径
与
05-23 1991
1.广度优先遍历的过程 思想：先遍历当前结点的全部邻接结点，然后依次遍历相邻结点的全部相邻结点 做法：使用队列 将0结点加入到队列中，将0从队列取出 将0结点还未遍历到的相邻结点入队 将1结点从队列取出，将1结点还未遍历到的相邻结点入队（此时没有） 将2结点从队列取出，将2结点还未遍历到的相邻结点入队（此时没有） 将5结点从队列取出，将5结点还未遍历到的相邻结点入队:3,4 将6结点从队列取出，将6结点还未遍历到的相邻结点入队（此时没有） 将3结点从队列取出，将3结点还未遍历到的相
图论之最小生成树 Prim算法和Kruskal算法
与
05-24 1394
1.最小生成树问题 最小生成树问题：一个图有V个顶点，找到V-1条边连接这V个顶点，使得总权值最小 最小生成树问题通常是针对带权无向图、连通图 如果图不是连通图：分别在每个连通分量上计算最小生成树---最小生成森林 应用：电缆布线设计、网络设计、电路设计 ...
图论之最短路径 Dijkstra算法、超级源点、反向建边
与
05-24 1243
1.最短路径问题 最短路径问题：求一个结点到另一个结点的权值总和最小的路径 对于无向图和有向图均是成立的 比如下图，求从结点0到结点6的最短路径 主要应用于：路径规划和工作任务规划 2.松弛操作 松弛操作是最短路径求解的核心 松弛操作：针对从0->1的最短路径，从0到1的权值是5， 此时我们尝试绕着从0->2->1，看下这样的走法所得到的权值是否小于直接从0->1 3.Dijkstra单源最短路径算法 这个算法的前提是图中不存在负权边（权值为负数） 算法
图的基础和表示
与
05-22 584
1.图的基础 图是由节点和边组成的 图的主要应用：交通运输、社交网络、互联网、工作安排、脑区活动、程序状态执行 图的分类：有向图和无向图；有权图和无权图；连通图和非连通图 图的连通性：如果从图的任意一个结点可以到另外任意一个结点，说明这个图是连通的，下面这个图不是完全连通的 简单图：没有自环边和平行边的（一般题目处理的都是简单图，如果没有说明是简单图，需要处理一下） 自环边：有自己到自己的一条路径 平行边：代表两个节点之前有多条连接路径。比如交通运输：从A点到B点有多条路径
非递归的深度优先遍历求联通分量的代码
04-20
以下是非递归的深度优先遍历求联通分量的代码示例： ``` #include #include #include using namespace std; const int N = 100; int n; int g[N][N]; // 图的邻接矩阵 bool st[N]; // 标记数组，记录每个点...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值