【LeetCode】100. 相同的树

原创 于 2025-11-05 22:06:13 发布 · 739 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#leetcode #算法 #职场和发展 #数据结构 #深度优先

程序员成长：技术、职场与思维模式实战指南 10w+人浏览 1.3k人参与

文章目录

100. 相同的树

题目描述

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

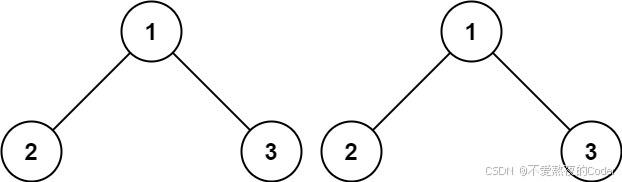
在这里插入图片描述

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

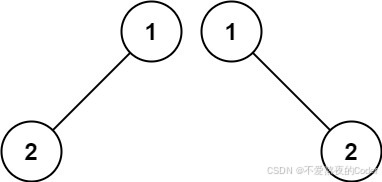
在这里插入图片描述

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

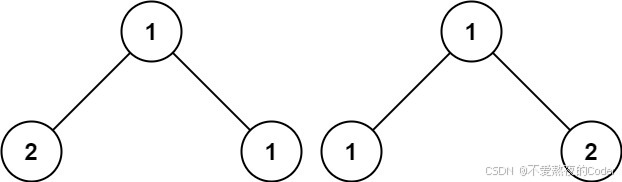
在这里插入图片描述

输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

  • 两棵树上的节点数目都在范围 [0, 100] 内
  • -10^4 <= Node.val <= 10^4

解题思路

问题深度分析

这是经典的树比较问题，也是树遍历的基础应用。核心在于同时遍历两棵树，比较它们的结构和节点值。

问题本质

给定两棵二叉树，判断它们是否完全相同。需要同时满足两个条件：

  1. 结构相同：两棵树的节点位置和连接关系完全一致
  2. 值相同：对应位置的节点值完全相同

这是一个树遍历 + 同步比较问题，需要同时访问两棵树的对应节点并进行比较。

核心思想

同步遍历两棵树：

  1. 递归比较：同时递归访问两棵树的对应节点
  2. 节点比较：
    • 如果两个节点都为nil，返回true
    • 如果只有一个为nil，返回false
    • 如果两个节点值不同，返回false
    • 如果两个节点值相同，继续比较左右子树
  3. 迭代比较：使用队列或栈同时遍历两棵树
  4. 序列化比较：将两棵树序列化为字符串，然后比较字符串

关键技巧：

  • 同时访问两棵树的对应节点
  • 先检查nil情况，避免空指针异常
  • 使用递归或迭代实现同步遍历
  • 利用队列实现BFS，利用栈实现DFS
关键难点分析

难点1：同步遍历

  • 需要同时访问两棵树的对应位置
  • 递归时两个树的递归深度必须同步
  • 迭代时需要同时维护两个队列或栈

难点2：边界条件处理

  • 两棵树都为空：返回true
  • 一棵树为空，另一棵不为空：返回false
  • 节点值不同：立即返回false

难点3：迭代实现

  • BFS需要同时维护两个队列
  • DFS需要同时维护两个栈
  • 需要确保两个队列/栈的操作同步
典型情况分析

情况1：完全相同的树

树p:          树q:
    1             1
   / \           / \
  2   3         2   3

比较过程：
1. 根节点：1 == 1 ✓
2. 左子树：2 == 2 ✓
3. 右子树：3 == 3 ✓
结果：true

情况2：结构不同

树p:          树q:
    1             1
   /               \
  2                 2

比较过程：
1. 根节点：1 == 1 ✓
2. 左子树：p.Left=2, q.Left=nil ✗
结果：false

情况3：值不同

树p:          树q:
    1             1
   / \           / \
  2   3         2   4

比较过程：
1. 根节点：1 == 1 ✓
2. 左子树：2 == 2 ✓
3. 右子树：3 != 4 ✗
结果：false

情况4：一棵树为空

树p:          树q:
    1            (空)

比较过程：
1. p != nil, q == nil ✗
结果：false
算法对比
算法时间复杂度空间复杂度特点
递归比较O(n)O(h)最优解法，代码简洁
BFS迭代O(n)O(n)层次遍历，易于理解
DFS迭代O(n)O(h)深度优先，空间优化
序列化比较O(n)O(n)思路新颖，但效率较低

注：n为节点数，h为树高度

算法流程图

主算法流程（递归比较）
graph TD
    A[isSameTree(p, q)] --> B{p == nil && q == nil?}
    B -->|是| C[return true]
    B -->|否| D{p == nil || q == nil?}
    D -->|是| E[return false]
    D -->|否| F{p.Val == q.Val?}
    F -->|否| E
    F -->|是| G[递归比较左子树]
    G --> H[递归比较右子树]
    H --> I{左右子树都相同?}
    I -->|是| J[return true]
    I -->|否| E
递归比较详细流程
是
否
是
否
否
是
是
否
比较节点p和q
两个都为nil?
返回true
只有一个为nil?
返回false
值相同?
比较p.Left和q.Left
比较p.Right和q.Right
左右子树都相同?
BFS迭代流程
否
是
是
否
是
否
否
是
初始化队列p_queue和q_queue
队列不空?
返回true
同时出队p_node和q_node
两个都为nil?
只有一个为nil?
返回false
值相同?
同时入队左右子节点

复杂度分析

时间复杂度详解

递归比较算法：O(n)

  • 需要访问两棵树的所有节点
  • 每个节点访问一次，进行常数时间比较
  • 最坏情况：需要比较所有节点
  • 总时间：O(n)

BFS迭代算法：O(n)

  • 需要遍历两棵树的所有节点
  • 每个节点入队和出队一次
  • 总时间：O(n)

DFS迭代算法：O(n)

  • 需要遍历两棵树的所有节点
  • 每个节点入栈和出栈一次
  • 总时间：O(n)
空间复杂度详解

递归比较算法：O(h)

  • 递归调用栈深度为树高度
  • 最坏情况（链状树）：O(n)
  • 最好情况（平衡树）：O(log n)

BFS迭代算法：O(n)

  • 需要队列存储节点
  • 最坏情况（完全二叉树）：队列大小为叶子节点数，约为n/2
  • 总空间：O(n)

DFS迭代算法：O(h)

  • 需要栈存储节点
  • 最坏情况（链状树）：O(n)
  • 最好情况（平衡树）：O(log n)

关键优化技巧

技巧1：递归比较（最优解法）
func isSameTree(p *TreeNode, q *TreeNode) bool {
    // 两棵树都为空
    if p == nil && q == nil {
        return true
    }
    
    // 一棵树为空，另一棵不为空
    if p == nil || q == nil {
        return false
    }
    
    // 节点值不同
    if p.Val != q.Val {
        return false
    }
    
    // 递归比较左右子树
    return isSameTree(p.Left, q.Left) && 
           isSameTree(p.Right, q.Right)
}

优势：

  • 时间复杂度：O(n)
  • 空间复杂度：O(h)
  • 代码简洁，逻辑清晰
  • 易于理解和实现
技巧2：BFS迭代比较
func isSameTree(p *TreeNode, q *TreeNode) bool {
    pQueue := []*TreeNode{p}
    qQueue := []*TreeNode{q}
    
    for len(pQueue) > 0 {
        // 同时出队
        pNode := pQueue[0]
        qNode := qQueue[0]
        pQueue = pQueue[1:]
        qQueue = qQueue[1:]
        
        // 检查nil
        if pNode == nil && qNode == nil {
            continue
        }
        if pNode == nil || qNode == nil {
            return false
        }
        if pNode.Val != qNode.Val {
            return false
        }
        
        // 同时入队左右子节点
        pQueue = append(pQueue, pNode.Left, pNode.Right)
        qQueue = append(qQueue, qNode.Left, qNode.Right)
    }
    
    return true
}

特点：层次遍历，适合需要逐层比较的场景

技巧3：DFS迭代比较
func isSameTree(p *TreeNode, q *TreeNode) bool {
    pStack := []*TreeNode{p}
    qStack := []*TreeNode{q}
    
    for len(pStack) > 0 {
        // 同时出栈
        n1 := len(pStack) - 1
        pNode := pStack[n1]
        qNode := qStack[n1]
        pStack = pStack[:n1]
        qStack = qStack[:n1]
        
        // 检查nil
        if pNode == nil && qNode == nil {
            continue
        }
        if pNode == nil || qNode == nil {
            return false
        }
        if pNode.Val != qNode.Val {
            return false
        }
        
        // 同时入栈左右子节点（注意顺序：先右后左）
        pStack = append(pStack, pNode.Right, pNode.Left)
        qStack = append(qStack, qNode.Right, qNode.Left)
    }
    
    return true
}

特点：深度优先遍历，空间复杂度O(h)

技巧4：序列化比较
func isSameTree(p *TreeNode, q *TreeNode) bool {
    return serialize(p) == serialize(q)
}

func serialize(root *TreeNode) string {
    if root == nil {
        return "#"
    }
    return fmt.Sprintf("%d,%s,%s", 
        root.Val, 
        serialize(root.Left), 
        serialize(root.Right))
}

特点：思路新颖，但效率较低（字符串拼接开销大）

边界条件处理

边界情况1：两棵树都为空
  • 处理：返回true
  • 验证：空树和空树相同
边界情况2：一棵树为空
  • 处理：返回false
  • 验证：空树和非空树不同
边界情况3：单节点树
  • 处理：比较根节点值
  • 验证：值相同返回true，值不同返回false
边界情况4：完全相同的树
  • 处理：递归比较所有节点
  • 验证：所有节点值相同，结构相同，返回true
边界情况5：结构相同但值不同
  • 处理：比较到第一个不同值时立即返回false
  • 验证：不需要比较所有节点，提前终止
边界情况6：结构不同
  • 处理：比较到第一个结构不一致时立即返回false
  • 验证：一个节点有子节点，另一个没有，立即返回false

测试用例设计

基础测试用例
  1. 完全相同：[1,2,3] vs [1,2,3] → true
  2. 结构不同：[1,2] vs [1,null,2] → false
  3. 值不同：[1,2,1] vs [1,1,2] → false
  4. 都为空：[] vs [] → true
进阶测试用例
  1. 单节点相同：[1] vs [1] → true
  2. 单节点不同：[1] vs [2] → false
  3. 一棵为空：[1] vs [] → false
  4. 完全二叉树相同：[4,2,6,1,3,5,7] vs [4,2,6,1,3,5,7] → true
  5. 链状树相同：[1,null,2,null,3] vs [1,null,2,null,3] → true
  6. 深度不同：[1,2] vs [1,2,null] → false

常见错误和陷阱

错误1：忘记检查nil
// 错误写法
if p.Val != q.Val {
    return false
}

// 正确写法
if p == nil && q == nil {
    return true
}
if p == nil || q == nil {
    return false
}
if p.Val != q.Val {
    return false
}

原因：直接访问p.Val或q.Val可能导致空指针异常

错误2：使用||而不是&&
// 错误写法
return isSameTree(p.Left, q.Left) || 
       isSameTree(p.Right, q.Right)

// 正确写法
return isSameTree(p.Left, q.Left) && 
       isSameTree(p.Right, q.Right)

原因：左右子树都必须相同，树才相同

错误3：BFS时队列不同步
// 错误写法
pQueue = append(pQueue, pNode.Left)
qQueue = append(qQueue, qNode.Left)
// 忘记入队右子节点

// 正确写法
pQueue = append(pQueue, pNode.Left, pNode.Right)
qQueue = append(qQueue, qNode.Left, qNode.Right)

原因：必须同时入队左右子节点，保持队列同步

错误4：DFS时栈顺序错误
// 错误写法：先左后右
pStack = append(pStack, pNode.Left, pNode.Right)

// 正确写法：先右后左（因为栈是后进先出）
pStack = append(pStack, pNode.Right, pNode.Left)

原因：栈是后进先出，需要先压右后压左才能先访问左

实用技巧

  1. 优先使用递归方法：代码简洁，逻辑清晰，易于理解和调试
  2. 提前终止：发现不同立即返回false，不需要继续比较
  3. nil检查放在前面：先处理nil情况，避免空指针异常
  4. BFS适合层次比较：如果需要逐层比较，使用BFS
  5. DFS适合深度比较：如果需要深度优先比较，使用DFS
  6. 迭代方法避免栈溢出：对于深度很大的树，使用迭代方法

进阶扩展

扩展1：判断子树是否相同
  • 判断一棵树是否是另一棵树的子树（需要先找到对应节点）
扩展2：判断树是否对称
  • 判断一棵树是否对称（镜像比较）
扩展3：判断树的结构是否相同
  • 只比较结构，不比较值
扩展4：找出不同的节点
  • 不仅返回true/false，还返回具体哪些节点不同

应用场景

  1. 数据结构验证：验证两个树结构是否相同
  2. 算法测试：测试树操作算法的正确性
  3. 代码审查：检查树构建代码的一致性
  4. 数据同步：检查两个数据源中的树结构是否一致
  5. 版本控制：比较不同版本的树结构

总结

判断两棵树是否相同是一个经典的树遍历 + 同步比较问题，核心在于：

  1. 同步遍历两棵树：同时访问对应位置的节点
  2. 先检查nil：避免空指针异常
  3. 递归比较最直观：代码简洁，易于理解
  4. 提前终止优化：发现不同立即返回，提高效率

完整题解代码

package main

import (
	"fmt"
)

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

// =========================== 方法一：递归比较（最优解法） ===========================
func isSameTree1(p *TreeNode, q *TreeNode) bool {
	// 两棵树都为空
	if p == nil && q == nil {
		return true
	}

	// 一棵树为空，另一棵不为空
	if p == nil || q == nil {
		return false
	}

	// 节点值不同
	if p.Val != q.Val {
		return false
	}

	// 递归比较左右子树
	return isSameTree1(p.Left, q.Left) && isSameTree1(p.Right, q.Right)
}

// =========================== 方法二：BFS迭代比较 ===========================
func isSameTree2(p *TreeNode, q *TreeNode) bool {
	pQueue := []*TreeNode{p}
	qQueue := []*TreeNode{q}

	for len(pQueue) > 0 {
		// 同时出队
		pNode := pQueue[0]
		qNode := qQueue[0]
		pQueue = pQueue[1:]
		qQueue = qQueue[1:]

		// 检查nil
		if pNode == nil && qNode == nil {
			continue
		}
		if pNode == nil || qNode == nil {
			return false
		}
		if pNode.Val != qNode.Val {
			return false
		}

		// 同时入队左右子节点
		pQueue = append(pQueue, pNode.Left, pNode.Right)
		qQueue = append(qQueue, qNode.Left, qNode.Right)
	}

	return true
}

// =========================== 方法三：DFS迭代比较 ===========================
func isSameTree3(p *TreeNode, q *TreeNode) bool {
	pStack := []*TreeNode{p}
	qStack := []*TreeNode{q}

	for len(pStack) > 0 {
		// 同时出栈
		n1 := len(pStack) - 1
		pNode := pStack[n1]
		qNode := qStack[n1]
		pStack = pStack[:n1]
		qStack = qStack[:n1]

		// 检查nil
		if pNode == nil && qNode == nil {
			continue
		}
		if pNode == nil || qNode == nil {
			return false
		}
		if pNode.Val != qNode.Val {
			return false
		}

		// 同时入栈左右子节点（注意顺序：先右后左，因为栈是后进先出）
		pStack = append(pStack, pNode.Right, pNode.Left)
		qStack = append(qStack, qNode.Right, qNode.Left)
	}

	return true
}

// =========================== 方法四：序列化比较 ===========================
func isSameTree4(p *TreeNode, q *TreeNode) bool {
	return serialize4(p) == serialize4(q)
}

func serialize4(root *TreeNode) string {
	if root == nil {
		return "#"
	}
	return fmt.Sprintf("%d,%s,%s",
		root.Val,
		serialize4(root.Left),
		serialize4(root.Right))
}

// =========================== 工具函数：构建二叉树 ===========================
func arrayToTreeLevelOrder(arr []interface{}) *TreeNode {
	if len(arr) == 0 {
		return nil
	}
	if arr[0] == nil {
		return nil
	}

	root := &TreeNode{Val: arr[0].(int)}
	queue := []*TreeNode{root}
	i := 1

	for i < len(arr) && len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]

		// 左子节点
		if i < len(arr) && arr[i] != nil {
			left := &TreeNode{Val: arr[i].(int)}
			node.Left = left
			queue = append(queue, left)
		}
		i++

		// 右子节点
		if i < len(arr) && arr[i] != nil {
			right := &TreeNode{Val: arr[i].(int)}
			node.Right = right
			queue = append(queue, right)
		}
		i++
	}

	return root
}

// =========================== 测试 ===========================
func main() {
	fmt.Println("=== LeetCode 100: 相同的树 ===\n")

	testCases := []struct {
		name     string
		p        *TreeNode
		q        *TreeNode
		expected bool
	}{
		{
			name:     "例1: [1,2,3] vs [1,2,3] - 完全相同",
			p:        arrayToTreeLevelOrder([]interface{}{1, 2, 3}),
			q:        arrayToTreeLevelOrder([]interface{}{1, 2, 3}),
			expected: true,
		},
		{
			name:     "例2: [1,2] vs [1,null,2] - 结构不同",
			p:        arrayToTreeLevelOrder([]interface{}{1, 2}),
			q:        arrayToTreeLevelOrder([]interface{}{1, nil, 2}),
			expected: false,
		},
		{
			name:     "例3: [1,2,1] vs [1,1,2] - 值不同",
			p:        arrayToTreeLevelOrder([]interface{}{1, 2, 1}),
			q:        arrayToTreeLevelOrder([]interface{}{1, 1, 2}),
			expected: false,
		},
		{
			name:     "都为空 - 相同",
			p:        arrayToTreeLevelOrder([]interface{}{}),
			q:        arrayToTreeLevelOrder([]interface{}{}),
			expected: true,
		},
		{
			name:     "单节点相同: [1] vs [1]",
			p:        arrayToTreeLevelOrder([]interface{}{1}),
			q:        arrayToTreeLevelOrder([]interface{}{1}),
			expected: true,
		},
		{
			name:     "单节点不同: [1] vs [2]",
			p:        arrayToTreeLevelOrder([]interface{}{1}),
			q:        arrayToTreeLevelOrder([]interface{}{2}),
			expected: false,
		},
		{
			name:     "一棵为空: [1] vs []",
			p:        arrayToTreeLevelOrder([]interface{}{1}),
			q:        arrayToTreeLevelOrder([]interface{}{}),
			expected: false,
		},
		{
			name:     "完全二叉树相同: [4,2,6,1,3,5,7] vs [4,2,6,1,3,5,7]",
			p:        arrayToTreeLevelOrder([]interface{}{4, 2, 6, 1, 3, 5, 7}),
			q:        arrayToTreeLevelOrder([]interface{}{4, 2, 6, 1, 3, 5, 7}),
			expected: true,
		},
		{
			name:     "链状树相同: [1,null,2,null,3] vs [1,null,2,null,3]",
			p:        arrayToTreeLevelOrder([]interface{}{1, nil, 2, nil, nil, nil, 3}),
			q:        arrayToTreeLevelOrder([]interface{}{1, nil, 2, nil, nil, nil, 3}),
			expected: true,
		},
		{
			name:     "结构细微不同: [1,2,3] vs [1,2,3,null]",
			p:        arrayToTreeLevelOrder([]interface{}{1, 2, 3}),
			q:        arrayToTreeLevelOrder([]interface{}{1, 2, 3, nil}),
			expected: true, // 层序遍历中，末尾的nil不影响树结构
		},
	}

	methods := map[string]func(*TreeNode, *TreeNode) bool{
		"递归比较":   isSameTree1,
		"BFS迭代":  isSameTree2,
		"DFS迭代":  isSameTree3,
		"序列化比较": isSameTree4,
	}

	for methodName, methodFunc := range methods {
		fmt.Printf("方法：%s\n", methodName)
		pass := 0
		for i, tc := range testCases {
			got := methodFunc(tc.p, tc.q)
			ok := got == tc.expected
			status := "✅"
			if !ok {
				status = "❌"
			}
			fmt.Printf("  测试%d(%s): %s\n", i+1, tc.name, status)
			if !ok {
				fmt.Printf("    输出: %v\n    期望: %v\n", got, tc.expected)
			} else {
				pass++
			}
		}
		fmt.Printf("  通过: %d/%d\n\n", pass, len(testCases))
	}
}
博客
使用Go语言实现线程安全的Map
11-25 876
自定义线程安全的SyncMap泛型支持：灵活适配不同类型的键值。线程安全：支持高并发场景的安全访问。可扩展性：易于添加更多功能，如合并操作、条件更新等。通过本文的实现与示例，希望您能更好地理解和应用线程安全Map，构建健壮的并发应用。
博客
使用 Go 语言封装 MinIO 相关操作
11-24 1105
MinIO 是一个高性能的对象存储服务，兼容 Amazon S3 API，广泛用于存储和管理海量数据。在实际开发中，封装一个便于使用的 MinIO 操作包，可以帮助我们简化操作逻辑，提高代码的可读性和复用性。初始化 MinIO 客户端上传文件下载文件列出文件删除文件获取文件的预签名 URL通过封装 MinIO 的常用操作，我们可以极大简化代码逻辑，提高开发效率。在实际项目中，可以根据需求进一步扩展功能，例如支持更多的操作、增加日志功能或通过配置文件动态加载参数等。
博客
Go语言开发的源代码行数统计工具
11-21 1331
是一个开源工具，用于统计各种编程语言的源代码文件数量和代码行数。它支持多种语言，易于扩展以包括自定义语言。简单易用，可以帮助开发者快速了解代码库并跟踪变化。页面下载预编译的二进制文件。
博客
使用gRPC基于Protobuf传输大文件或数据流
05-10 2738
在gRPC中，服务和消息的定义是通过.proto文件进行的。例如，定义一个文件传输服务，可以在这里定义了一个服务，包含了一个Upload方法，该方法接受一个FileChunk类型的流，并返回一个状态。
博客
极光推送Go语言服务端SDK
12-31 1241
jpush-api-golang-client项目地址：https://github.com/Scorpio69t/jpush-api-golang-client概述JPush’s Golang client library for accessing JPush APIs. 极光推送的 Golang 版本服务器端 SDK。该项目参考ylywyn结合极光推送官方文档而来。(原项目年久失修，有很多新特性都没有提供，本项目旨在将其完善，方便大家使用，后续会持续更新，不足之处欢迎大家指正，谢谢~)参考R
博客
HackRF-AIS信号的采集与解调
10-25 2291
目录AIS信号采集与解调1、硬件设备2、系统准备3、软件准备4、进行实验（需要去有船只经过的江边才能采集到信号，本次实验于重庆嘉陵江边进行）5、AIS信息解译AIS解调后数据源可去一下连接获取AIS信号采集与解调1、硬件设备​ 硬件设备采用HackRF One，HackRF是一款全开源的硬件项目，其目的主要是为了提供廉价的SDR(软件定义无线电)方案，作者Mike Ossmann在第一版HackRF Jawbreaker时通过Kickstart融资成功，之后Mike Ossmann开始进行了第二版Ha
博客
c/c++ 实现三角函数（不使用库函数） sin/cos/tan/cot
03-23 4923
在许多嵌入式系统或计算平台中，可能不方便使用标准数学库函数。在本篇博客中，我们将使用 泰勒展开 来实现常见的三角函数：sin(x)、cos(x)、tan(x) 和 cot(x)，而不依赖任何库函数。通过手动实现这些数学公式，我们可以更好地理解三角函数的计算原理，同时为那些受限的环境提供一种实现方案。泰勒展开是数学中一个非常重要的公式，它能够将任何在某点可导的函数展开为一个无限级数。对于三角函数，我们可以利用其在0点的泰勒级数展开来近似计算函数值。sinxx−x33!x55!−。
博客
【LeetCode】101. 对称二叉树
11-05 533
文章摘要： 本题要求判断二叉树是否轴对称。核心思路是递归或迭代比较左右子树的镜像位置：左子树的左节点对应右子树的右节点，左子树的右节点对应右子树的左节点。递归法代码简洁，时间复杂度O(n)，空间复杂度O(h)；迭代法（BFS/DFS）虽然空间复杂度可能达到O(n)，但更直观易懂。关键点在于处理边界条件（空节点比较）和同步遍历镜像节点。典型测试用例包括完全对称树、结构不对称树和单节点树等情况。最优解推荐递归实现，既高效又易于理解。
博客
【LeetCode】99. 恢复二叉搜索树
11-04 409
二叉搜索树恢复问题要求交换两个错误节点的值来修复BST。通过中序遍历的递增性质，可以高效检测出错误节点：当出现前节点值大于当前节点值时记录逆序对。相邻交换只需交换单个逆序对，非相邻交换则需交换第一个逆序对的前节点和最后一个逆序对的后节点。最优解法采用O(1)空间的Morris遍历，在遍历过程中动态修改树结构并记录错误节点，最后进行值交换。时间复杂度O(n)，空间复杂度O(1)。
博客
【LeetCode】98. 验证二叉搜索树
11-04 638
本文介绍了验证二叉搜索树(BST)的方法。BST需满足节点左子树严格小于当前节点，右子树严格大于当前节点，且左右子树也是BST。解题核心在于验证三个约束条件：节点值在正确范围内、子树符合BST定义、中序遍历结果严格递增。提供了三种算法：1）递归传递上下界（最优解，O(n)时间，O(h)空间）；2）中序遍历递归验证（利用BST中序递增性质）；3）中序遍历迭代实现（避免递归栈溢出）。关键难点在于处理节点值的严格大小关系和整数边界问题。通过维护每个节点的合理范围，可以高效判断是否为有效BST。
博客
【LeetCode】97. 交错字符串
11-02 1132
本文探讨了交错字符串问题，即判断字符串s3是否能由s1和s2交替组合而成。通过动态规划方法解决该问题，其中状态dp[i][j]表示s1前i个字符和s2前j个字符能否组成s3前i+j个字符。状态转移方程考虑字符匹配情况，并可通过滚动数组优化空间至O(n)。此外，还介绍了记忆化递归和BFS搜索两种替代解法。关键点包括：长度验证、保持字符相对顺序、以及多种路径选择的处理方式。时间复杂度为O(mn)，其中m和n分别为s1和s2的长度。
博客
【LeetCode】95. 不同的二叉搜索树 II
11-02 801
本文讨论了生成所有由n个不同节点构成的二叉搜索树的问题。核心思路是通过递归分治，枚举每个数字作为根节点，并递归构造左右子树的所有可能组合，最后将左右子树进行笛卡尔积组合。文章详细分析了二叉搜索树的性质、递归构造过程（附流程图解）、记忆化优化策略以及复杂度比较。特别强调了当n=3时的5种可能构造示例，并提供了递归终止条件、根节点选择、子树组合等关键实现要点。该问题时间复杂度与卡塔兰数相关，记忆化优化可将时间复杂度降至O(Cn)。
博客
【LeetCode】94. 二叉树的中序遍历
10-30 747
二叉树的中序遍历要求按照左子树-根节点-右子树的顺序访问节点，输出节点值序列。题目给出了四种实现方法：递归法（最简单直观）、迭代法（显式栈模拟递归）、颜色标记法（统一遍历模板）和Morris遍历法（O(1)空间复杂度）。其中递归法代码最简洁，时间复杂度均为O(n)，空间复杂度递归和显式栈为O(h)（树高），Morris遍历最优为O(1)。关键点包括处理空树、单节点等边界情况，Morris遍历需注意维护线索指针。
博客
【LeetCode】92. 反转链表 II
10-30 1105
摘要 题目要求在单链表中反转指定区间[left, right]的节点。主要方法包括：头插法（最优，O(n)时间O(1)空间）、常规反转子链后接回、递归解法（reverseN + 偏移）和栈辅助法。关键点在于精确定位边界节点，处理指针连接顺序。使用哑节点简化头部操作，注意边界条件如left=1或right为链表尾部等情况。各种方法时间复杂度均为O(n)，但空间复杂度不同，头插法和常规反转最优。
博客
【LeetCode】91. 解码方法
10-28 1018
本文介绍了解决"解码方法"问题的动态规划解法。题目要求将数字字符串解码为字母组合（1-26对应A-Z），计算所有可能的解码方式。核心思路是使用动态规划，状态转移考虑单字符和双字符两种解码方式，并处理前导零等边界情况。时间复杂度O(n)，空间复杂度可优化至O(1)。示例展示了不同字符串的解码过程，如"226"有3种解码方式，而"06"因前导零无法解码。
博客
【LeetCode】90. 子集 II
10-28 979
题目要求返回包含重复元素的整数数组的所有可能子集，且解集中不能有重复子集。解题关键在于回溯算法结合去重策略：先对数组排序使相同元素相邻，然后在回溯过程中跳过重复元素。时间复杂度为O(2^n)，空间复杂度为O(n)。最优解法是回溯+去重，通过排序预处理和剪枝优化来避免生成重复子集。典型示例如输入[1,2,2]应输出[[],[1],[1,2],[1,2,2],[2],[2,2]]。
博客
【LeetCode】89. 格雷编码
10-27 1110
本文介绍了n位格雷码的生成问题。格雷码要求相邻整数二进制表示仅一位不同，首尾也需满足这一条件。关键解法包括对称反射法和位运算公式法，时间复杂度均为O(2^n)。对称反射法通过递归构造n-1位格雷码并镜像反射，添加最高位实现；位运算公式则利用i^(i>>1)快速生成。文章详细分析了算法流程、复杂度、边界条件及常见错误，并提供了多种实现方式（递归/迭代）。典型示例展示了n=1时返回[0,1]，n=2时返回[0,1,3,2]等有效序列。
博客
【LeetCode】88. 合并两个有序数组
10-27 564
摘要 合并两个有序数组问题要求将nums2合并到nums1中，并保持非递减顺序。最优解法采用双指针逆序遍历策略：初始化三个指针分别指向nums1、nums2的有效元素末尾和合并后的末尾位置；从后往前比较元素，较大者放入nums1末尾；最终处理剩余元素。该方法时间复杂度O(m+n)，空间复杂度O(1)，完美满足原地合并需求。关键点在于逆序处理避免元素覆盖，并妥善处理边界条件和剩余元素。相比正序遍历需要额外空间或排序算法效率低的问题，这种解法在时间和空间复杂度上均为最优。
博客
【LeetCode】87. 扰乱字符串
10-22 711
摘要 本文探讨了判断字符串是否为扰乱字符串的问题。扰乱字符串是通过递归分割和交换操作生成的，要求判断给定字符串s2是否可由s1通过该算法得到。核心解法采用动态规划，定义三维状态dp[i][j][k]表示子串匹配状态，时间复杂度O(n^4)，空间复杂度O(n^3)。文章详细分析了算法思路、关键难点和优化技巧，并对比了递归、记忆化等不同解法。典型示例展示了字符串分割与交换的转换过程，帮助理解扰乱字符串的生成机制。
博客
【LeetCode】86. 分隔链表
10-22 336
这篇题解介绍了如何将链表按给定值x进行分隔，要求小于x的节点出现在大于等于x的节点之前，并保持相对位置。主要采用双链表法，通过创建两个虚拟链表分别存储两个分区，最后连接两个分区。该方法时间复杂度O(n)，空间复杂度O(1)，是最优解法。文章还分析了其他解法（数组法、递归法）的优缺点，并提供了详细的算法流程图和代码实现。关键点在于使用双指针维护两个分区，确保相对位置不变。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值