【转载】EEG中常用的功能连接指标汇总

EEG中常用的功能连接指标汇总

功能连接（Functional connectivity, FC）可以说是EEG研究中的一个非常重要的方法。对于正常的大脑高级认知功能来说，往往并不仅仅是单独的某个脑区在起作用，而是更加依赖于不同脑区之间的相互协同工作，因此研究不同脑区的功能连接对我们理解大脑的大脑高级认知功能机制来说非常重要。那么究竟什么是功能连接，如何定量测量不同脑区之间的功能连接呢？所谓的功能连接其实就是用某种方法来测量两种信号之间的依赖或相关程度。在EEG领域中，研究者提出了非常丰富的算法来测定两种信号之间的相关程度，即所谓的功能连接指标。不同的功能连接指标具有各自的特点，因此研究者需要根据各自数据或者欲解决的问题来选择合适的功能连接指标。笔者在这里会陆续分几篇文章对EEG中常用的功能连接指标的计算方法、优缺点进行系统梳理，希望对大家有帮助。

1.皮尔森相关系数（Pearson correlation coefficient）
皮尔森相关系数r应该是最简单的功能连接指标，对于信号x、y，两者的皮尔森相关系数r计算公式如下：

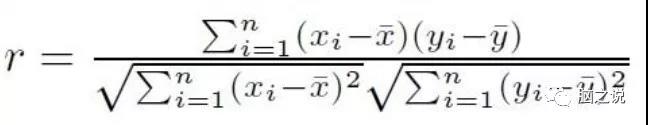
r的取值范围[-1 1],因此皮尔森相关系数可以测量出两个信号是正相关还是负相关，并且绝对值越大，相关性越强。但是，皮尔森相关系数只能测量两个信号的线性相关性。

2.波谱相干（Spectral coherence）
相干，有时也被称为magnitude-squared coherence，其测量的是两个信号在频域内的相关程度，计算公式如下：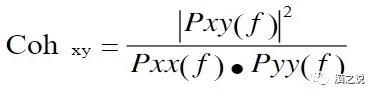

其中Pxy表示信号x、y的互谱密度（cross-spectral density），Pxx和Pyy分别表示x、y的自谱密度，即功率谱密度。Cohxy的取值范围[0 1]，值越大说明两个信号在频率f处的相关程度越大。但是，与皮尔森相关系数类似，相干也只能测量两个信号的线性相关性。

3.互信息（Mutual information, MI）
互信息MI是一种基于信息论的功能连接方法，它测定的是一种信号中包含的关于另一个信号量的信息量，MI的计算方法如下：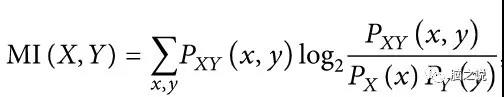

其中Pxy表示信号x、y的联合概率分布，Px、Py分别表示信号x、y的概率分布。上述公式计算出来的MI的取值范围为大于等于0的实数，因此，有时我们需要对MI进行归一化，使得其取值范围在[0 1]之间，归一化的MI计算公式如下：

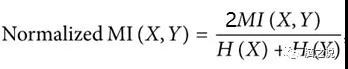
其中H（X）和H（Y）分别表示信号x、y的熵。
与皮尔森相关系数和相干分析不同，MI最大的优点是可以同时检测两个信号的线性和非线性相关性，但是MI计算准确度容易受到信号中噪声以及信号长度的影响。

4.相锁值（Phase Locking Value, PLV）
相锁值PLV是基于相位的功能连接方法，其实际测量的是两个通道信号的相位差，计算方法如下：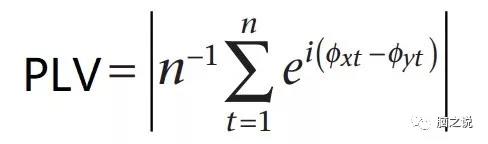

其中n表示时间点，φxt、φyt分别表示信号x、y在时间点t处的相角。
PLV的取值范围为[0 1]，值越大表示两个信号之间的相位同步程度越强。但是PLV对体积传导效应（volume conduction effect）比较敏感。

5.相滞指数（Phase lag index，PLI）
与PLV相似，PLI也是基于相位的功能连接方法，可以用来测量两个通道信号的相同步程度，其计算方法如下：
其中，N表示时间点，φrel表示两个通道信号在时间tn处的相位差，sign是一个符号函数，当自变量为正值时其输出为1，当自变量为负值时其结果为-1，对于0其结果也是0.
PLI的取值范围为[0 1]，值越大表示两个信号之间的相位同步程度越强。PLI最主要的优点是对体积传导效应（volume conduction effect）不敏感，但是其对噪声似乎比较敏感。

6.部分有向相干（Partial directed coherence, PDC）
PDC是一种基于格兰杰因果关系的多变量有效连接测量方法，与前面介绍的其他功能连接方法不同，PDC是测量通道信号之间的因果影响，因此是有方向性的。对于一个N通道的EEG信号X(n)=[x1(n),x2(n), x3(n), …, xN(n)]T，其可以用一个多变量的自回归模型MVAR来描述：

其中p是MVAR的order，Ar表示系数矩阵，W(n)表示高斯白噪声。
p可以通过Akaike information criterion (AIC)来求解，而通过Yule-Walker方程，可以把Ar求解出来。当求得Ar之后，那么就可以得到A(f):

其中I表示identity matrix。
那么，频率f处从通道j到通道i的有向信息流即PDC值可以用以下公式来求解：

其中Aij(f)表示A(f)矩阵的元素，*表示矩阵转置和复共轭。
PDC值的范围[0 1]，值越大表示从通道j到i的信息流动越强

7.有向传递函数（Direct Transfer Function, DTF）
与PDC类似，DTF也是一种基于格兰杰因果关系的多变量有效连接测量方法，DTF的计算过程也与PDC类似，唯一区别在于DTF的计算用到了上述A(f)的逆矩阵，我们这里记为H(f)，那么DTF定义为：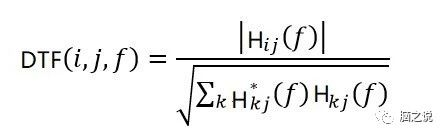

同样，DTF取值范围在[0 1]。与PDC相比，DTF主要问题可能是会检测到通道之间的间接因果连接，因此会产生虚假连接，而PDC只检测通道之间的直接连接。

8.其他功能连接指标
除了在《系列1》和本文上述介绍的这些功能连接指标，还有很多其他的功能连接的指标，如同步似然指数（Synchronization Likelihood, SL）、转移熵（Transfer Entropy, TE）、部分转移熵（Partial Transfer Entropy, PTE）、相位斜率指数(Phase Slope Index, PSI)、加权PLI（Weighted Phase-Lag Index, WPLI）、部分MI(Partial Mutual Information, PMI)等。而有些功能连接指标的计算原理笔者也并不是十分了解，在这里就不展开介绍，以免误人子弟。如果想对各种各样的功能连接指标有一个系统的了解，笔者推荐HERMES工具包。HERMES是由西班牙马德里技术大学（Technical University of Madrid）的Centre for Biomedical Technology团队研发的基于Matlab的开源EEG工具包，其主要的功能和特点是计算基于各种方法的功能连接，HERMES官方网址：http://hermes.ctb.upm.es/