【机器学习】无监督学习系列-python实战

最新推荐文章于 2025-03-06 15:04:29 发布

AI蜗牛车

最新推荐文章于 2025-03-06 15:04:29 发布

阅读量894

点赞数 1

文章标签：聚类人工智能机器学习数据挖掘深度学习

转自：ChallengeHub

A.监督学习

1.EDA（Exploratory Data Analysis）
2.K-Nearest Neighbors（KNN）
3.线性回归
4.交叉验证（CV）
5.正则化回归
6.ROC曲线与逻辑回归
7.超参数调优
8.SVM

B.无监督学习

1.Kmeans聚类
2.聚类效果评价
3.标准化
4.层次分析法
5.T-分布随机近邻嵌入(T-SNE)
6.主成分分析（PCA）

监督学习

可以查看机器学习全面教程-有监督学习篇

无监督学习

无监督学习: 它使用无标记的数据，并从无标记的数据中发现隐藏的模式信息。例如，有些骨科病人数据没有标签，你不知道哪个骨科病人是正常的，哪个是不正常的。

1.Kmeans聚类

让我们尝试我们的第一个无监督的方法，即KMeans Cluster
KMeans聚类:该算法基于所提供的特征迭代地将每个数据点分配给K组中的一个。基于特征相似性对数据点进行聚类
KMeans(n_clusters = 2): n_clusters = 2表示创建2个簇群

先看数据的分布

# As you can see there is no labels in data
data = pd.read_csv('column_2C_weka.csv')
plt.scatter(data['pelvic_radius'],data['degree_spondylolisthesis'])
plt.xlabel('pelvic_radius')
plt.ylabel('degree_spondylolisthesis')
plt.show()

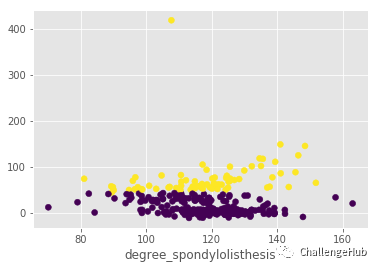
再看通过Kmeans聚类分类效果

# KMeans Clustering
data2 = data.loc[:,['degree_spondylolisthesis','pelvic_radius']]
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 2)
kmeans.fit(data2)
labels = kmeans.predict(data2)
plt.scatter(data['pelvic_radius'],data['degree_spondylolisthesis'],c = labels)
plt.xlabel('pelvic_radius')
plt.xlabel('degree_spondylolisthesis')
plt.show()

2.聚类效果评价

我们把数据分成两组。这是正确的聚类吗? 为了评估聚类效果，我们将使用交叉表。

有两个集群，分别是0和1
标签0包括138例异常患者和100例正常患者
标签1包括72例异常患者和0例正常患者
两个簇群中大多数为异常患者。

# cross tabulation table
df = pd.DataFrame({'labels':labels,"class":data['class']})
ct = pd.crosstab(df['labels'],df['class'])
print(ct)

上面存在一个问题是，我们事先知道了数据中是几分类问题，但是如果不知道呢? 那这有点像KNN或回归中的超参数问题了。

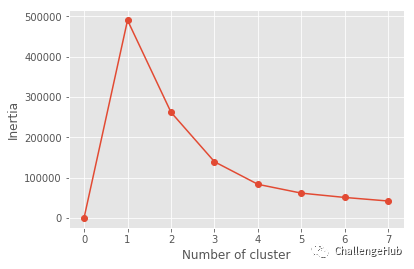
inertia:簇群与每个样本之间的距离
更小的inertia意味着更多的簇
簇群的最佳数量是多少?
更小的inertia，没有太多的簇群平衡，所以我们可以选择elbow

# inertia
inertia_list = np.empty(8)
for i in range(1,8):
    kmeans = KMeans(n_clusters=i)
    kmeans.fit(data2)
    inertia_list[i] = kmeans.inertia_
plt.plot(range(0,8),inertia_list,'-o')
plt.xlabel('Number of cluster')
plt.ylabel('Inertia')
plt.show()

3.标准化

标准化对于监督学习和非监督学习都很重要，可以消除量纲影响

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
scalar = StandardScaler()
kmeans = KMeans(n_clusters = 2)
pipe = make_pipeline(scalar,kmeans)
pipe.fit(data3)
labels = pipe.predict(data3)
df = pd.DataFrame({'labels':labels,"class":data['class']})
ct = pd.crosstab(df['labels'],df['class'])
print(ct)

4.层次分析法

竖线是簇
树状图高度: 归并簇之间的距离
方法= 'single': 表示簇的最近点

from scipy.cluster.hierarchy import linkage,dendrogram

merg = linkage(data3.iloc[200:220,:],method = 'single')
dendrogram(merg, leaf_rotation = 90, leaf_font_size = 6)
plt.show()

5.T-SNE

学习率:正常情况下50-200
T-sne只有fit_transform

from sklearn.manifold import TSNE
model = TSNE(learning_rate=100)
transformed = model.fit_transform(data2)
x = transformed[:,0]
y = transformed[:,1]
plt.scatter(x,y,c = color_list )
plt.xlabel('pelvic_radius')
plt.xlabel('degree_spondylolisthesis')
plt.show()

6.PCA

基本的降维技术
第一步是去相关:
- 旋转数据样本以使其与轴对齐
- 移动数据样本，使其均值为零
- 没有信息丢失
- Fit():学习如何移动样本
- Transform():应用学到的转换。也可以应用测试集
由此产生的PCA特征不是线性相关的
主成分:是方差方向

# PCA
from sklearn.decomposition import PCA
model = PCA()
model.fit(data3)
transformed = model.transform(data3)
print('Principle components: ',model.components_)

# PCA variance
scaler = StandardScaler()
pca = PCA()
pipeline = make_pipeline(scaler,pca)
pipeline.fit(data3)

plt.bar(range(pca.n_components_), pca.explained_variance_)
plt.xlabel('PCA feature')
plt.ylabel('variance')
plt.show()

第二步:内在维度: 需要特征数量来近似数据背后的基本思想
当样本具有任意数量的特征时，主成分分析识别内在维数
内在维度 = 具有显著方差的PCA特征的数量
为了选择内在维度，尝试所有的方法并找到最佳的精度

# apply PCA
pca = PCA(n_components = 2)
pca.fit(data3)
transformed = pca.transform(data3)
x = transformed[:,0]
y = transformed[:,1]
plt.scatter(x,y,c = color_list)
plt.show()

建议阅读：

高考失利之后，属于我的大学本科四年

【资源分享】对于时间序列，你所能做的一切.

【时空序列预测第一篇】什么是时空序列问题？这类问题主要应用了哪些模型？主要应用在哪些领域？

【AI蜗牛车出品】手把手AI项目、时空序列、时间序列、白话机器学习、pytorch修炼

公众号：AI蜗牛车

保持谦逊、保持自律、保持进步



个人微信
备注：昵称+学校/公司+方向
如果没有备注不拉群！
拉你进AI蜗牛车交流群