矩阵分析重点归纳

最新推荐文章于 2023-09-11 10:14:33 发布

Hillbox

最新推荐文章于 2023-09-11 10:14:33 发布

阅读量5.8k

点赞数 25

分类专栏：矩阵分析

本文链接：https://blog.csdn.net/qq_33514421/article/details/112549822

版权

矩阵分析专栏收录该内容

3 篇文章 7 订阅

订阅专栏

免责声明

本文仅个人学习笔记，请谨慎参考，如有错误欢迎批评指正。

重点概括

不仅包括今年的期末重点，还有往年期末卷子的考点。

1、线性空间的判断。书P1

1、加法封闭性

2、乘法封闭性

3、满足8条运算规则： $(1) \alpha +\beta = \beta +\alpha$ ； $(2) (\alpha +\beta)+\gamma = \alpha +(\beta+\gamma )$ ； $(3) \alpha +0=\alpha$ ； $(4) \alpha +\beta =0, \beta =-\alpha$ ； $(5) 1\alpha =\alpha$ ； $(6) k(l\alpha )=(kl)\alpha$ ； $(7) (k+l)\alpha =k\alpha +l\alpha$ ； $(8) k(\alpha +\beta)=k\alpha +k\beta$ ；

2、维数。书P3

基中向量的个数。

dim(V1+V2) = dimV1 + dimV2 - dim(V1交V2)

3、正规矩阵。书P36

满足 $A^{H}A=AA^{H}$ 的矩阵A。

4、向量范数。书P88

1范数： $||\alpha ||_{1}=\sum_{i=1}^{n}|x_{i}|$ = 所有元素的模和

2范数： $||\alpha ||_{2}=\sqrt{\sum_{i=1}^{n}|x_{i}|^{2}}$ = 所有元素的模的平方和开根号

无限范数： $||\alpha ||_{\infty }= \underset{1\leq i\leq n}{max}\left | x_{i} \right |$ = 所有元素的模的最大者

5、矩阵范数。书P91、93

1范数： $||A||_{1}=$ 列模和最大者

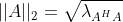
2范数： $||A||_{2}=\sqrt{\lambda _{A^{H}A}}$ $= \sqrt{\lambda _{AA^{H}}}$ （ $\lambda _{A^{H}A}$ 是 $A^{H}A$ 或 $AA^{H}$ 的最大特征值）

无限范数： $||A||_{\infty }=$ 行模和最大者

F范数： $||\alpha ||_{F}=\sqrt{\sum_{i,j=1}^{n}|a_{ij}|^{2}}=\sqrt{tr(A^{H}A)}$ = 所有元素的模的平方和开根号= $A^{H}A$ 的迹开根号

6、奇异值。书P84

$A^{H}A的特征值$ 或 $AA^{H}$ 的所有特征值开根号

7、谱半径。书P130

矩阵特征值的模的最大数。

$\rho (A^{2}) = \rho (A)*\rho (A)$

$\rho (A) \leq \left \| A \right \|$ 谱半径小于任何A的范数

8、广义矩阵。书P137 习题五 7

给定矩阵A，

若A为行满秩，则 $A^{+}=A^{H}(AA^{H})^{-1}$

若A为列满秩，则 $A^{+}=(A^{H}A)^{-1}A^{H}$

9、圆盘定理。书P129

矩阵有多少行，就算多少个圆盘。

对于每一行，在对角线上的数 x+yi 的 (x,y) 作为圆盘的圆心，在这一行中，除去对角线上的数的其他数的模相加作为圆盘的半径。

算出所有行的圆盘后，矩阵的特征值的范围就在圆盘的并集里面。

10、行列式因子、不变因子、初级因子。书P52-53

给定矩阵A，算出它的特征矩阵 $(\lambda E-A)$

1、行列式因子：n阶矩阵有n阶行列式因子，用 $D_{i}(\lambda)$ 表示。

$D_{1}(\lambda)$ 是特征矩阵 $(\lambda E-A)$ 的所有1阶行列式的公因子；

$D_{2}(\lambda)$ 是特征矩阵 $(\lambda E-A)$ 的所有2阶行列式的公因子......；

$D_{n}(\lambda)$ 是特征矩阵 $(\lambda E-A)$ 的n阶行列式的公因子（直接就是特征多项式）。

2、不变因子：用 $d_{i}(\lambda)$ 表示。

$d_{1}(\lambda)=D_{1}(\lambda)$ ，

$d_{2}(\lambda)=\frac{D_{2}(\lambda)}{D_{1}(\lambda)}$

......

$d_{n}(\lambda)=\frac{D_{n}(\lambda)}{D_{n-1}(\lambda)}$

3、初级因子：找出非常数的不变因子，把因式分解开，有次方的就不用分解开了。P53的例子讲的很清楚。

11、史密斯标准型

Smith标准型是对角矩阵，要求矩阵经过一系列初等行变换或列变换，使对角线上元素前一行是后一行的因子。

12、约当标准型。书P55

任何矩阵都相似于一个约当标准型。

写出特征矩阵，求出行列式因子、不变因子、初级因子。对于每个初级因子，求 $m = n-r(\lambda E-A)$ ，m等于多少，该初级因子就有多少个约当块。

13、最小多项式。书P59

A的特征多项式是A的零化多项式，而在A的零化多项式中，次数最低的首一多项式称为A的最小多项式。

求法是，先算特征多项式，如果它没有次方，那最小多项式就是特征多项式。如果有次方那么就一个一个把A和E带入验算是不是零。

比如特征多项式= $\lambda (\lambda -1)^{3}$ ，则要按顺序从 $\lambda (\lambda -1)$ 、 $\lambda (\lambda -1)^{2}$ 、 $\lambda (\lambda -1)^{3}$ ，把 $\lambda$ 换成A，1变成E，带入计算是否等于零，首次等于零的那个就是最小多项式。

14、矩阵函数 f(A)和f(At)。书P111-113

1、求特征多项式

2、求最小多项式

3、根据最小多项式的次数设等式

4、特征值分别带入方程式，联立方程组

5、求得的解带入等式

15、最小二乘法。书P32

AX=B，两边同时乘 $A^{T}$ ，即 $A^{T}AX=A^{T}B$ ，求出解。

16、QR分解

A=QR，Q是A的正交单位化向量，求出Q即可得到R。

正交化：

$\beta _{1}=\alpha _{1}$

$\beta _{2} = \alpha _{2} - \frac{<\alpha _{2},\beta _{1}>}{<\beta 1, \beta _{1}>}\beta _{1}$

$\beta _{3} = \alpha _{3} - \frac{<\alpha _{3},\beta _{2}>}{<\beta 2, \beta _{2}>}\beta _{2} - \frac{<\alpha _{3},\beta _{1}>}{<\beta 1, \beta _{1}>}\beta _{1}$

单位化：

$e_{i}=\frac{1}{\left \| \beta_{i} \right \|}\beta_{i}$

17、奇异值分解

给定矩阵A，

1、Q= $AA^{T}$ 的特征向量正交单位化

2、P= $A^{T}A$ 的特征向量单位化

3、奇异值=特征值开根号，按照特征向量的顺序放D的对角线上

4、 $A=Q\begin{bmatrix} D & 0\\ 0 & 0 \end{bmatrix}P^{T}$

Hillbox

关注

25
点赞
踩
119

收藏

觉得还不错? 一键收藏
5
评论
矩阵分析重点归纳

免责声明本文仅个人学习笔记，请谨慎参考，如有错误欢迎批评指正。重点概括不仅包括今年的期末重点，还有往年期末卷子的考点。1、线性空间的判断。书P11、加法封闭性2、乘法封闭性3、满足8条运算规则：；；；；；；；；2、维数。书P3基中向量的个数。dim(V1+V2) = dimV1 + dimV2 - dim(V1交V2)3、正规矩阵。书P36满足的矩阵A。4、向量范数。书P881范数：= 所有元素的模和2范数：= 所有元素的模的平方..
复制链接

扫一扫