Linear Algebra
1、矩阵的值域(Range)以及零空间(nullspace)
矩阵的值域,表示成
R
(
A
)
R(A)
R(A),是所有
R
m
R^{m}
Rm空间中的可以由矩阵
A
A
A列向量线性组合的向量组成的集合,即:
R
(
A
)
=
{
A
x
∣
x
∈
R
n
}
R(A)=\{Ax|x\in \R^{n}\}
R(A)={Ax∣x∈Rn}
矩阵的值域构成了一个
R
m
R^{m}
Rm的子空间。它的空间维度是矩阵
A
A
A的秩,表示成
r
a
n
k
A
rank\ A
rank A。
矩阵
A
A
A的零空间(有些地方叫解空间),表示成
N
(
A
)
N(A)
N(A),是所有的满足
A
x
=
0
Ax=0
Ax=0的
x
x
x向量的集合,即:
N
(
A
)
=
{
x
∣
A
x
=
0
}
N(A)=\{x|Ax=0\}
N(A)={x∣Ax=0}
也因此
N
(
A
)
∈
R
n
N(A)\in \R^{n}
N(A)∈Rn,它的空间维度是
m
−
R
a
n
k
(
A
)
m-Rank(A)
m−Rank(A)。
大体我是这么尝试去理解的:
矩阵A引起的正交分解
如果
V
V
V是
R
n
R^{n}
Rn的子空间,那么它的正交补(orthogonal complement),表示成
V
⊥
=
{
x
∣
z
T
x
=
0
f
o
r
a
l
l
z
∈
V
}
V^{\bot}=\{x|z^{T}x=0\ for\ all\ z\in V\}
V⊥={x∣zTx=0 for all z∈V}(
V
⊥
⊥
=
V
V^{\bot\bot}=V
V⊥⊥=V)
关于正交,一个基本的结论是:
N
(
A
)
=
R
(
A
T
)
⊥
,
R
(
A
)
=
N
(
A
T
)
⊥
N(A)=R(A^{T})^{\bot},R(A)=N(A^{T})^{\bot}
N(A)=R(AT)⊥,R(A)=N(AT)⊥
这个结论也可以描述成:
N
(
A
)
⊕
⊥
R
(
A
T
)
=
R
n
N(A)\overset{\bot}{\oplus} R(A^{T})=R^{n}
N(A)⊕⊥R(AT)=Rn
这里的符号
⊕
⊥
\overset{\bot}{\oplus}
⊕⊥叫做正交直和,上述式子描述的是对A进行正交分解。
直和:
若
W
1
⋂
W
2
=
0
,
那
么
W
1
+
W
2
就
是
直
和
,
记
作
W
1
⊕
W
2
若W_{1}\bigcap W_{2}={0},那么W_{1}+W_{2}就是直和,记作W_{1}\oplus W_{2}
若W1⋂W2=0,那么W1+W2就是直和,记作W1⊕W2
2、对称矩阵的特征值分解
若
A
∈
S
n
A\in S^{n}
A∈Sn,即
A
A
A是一个对称
n
×
n
n\times n
n×n的方阵,则
A
A
A可以被分解成:
A
=
Q
Λ
Q
T
A=Q\Lambda Q^{T}
A=QΛQT
其中
Q
Q
Q是正交矩阵,即
Q
Q
T
=
E
QQ^{T}=E
QQT=E,
Λ
\Lambda
Λ是对角矩阵,其中的每一个元素都是矩阵
A
A
A的特征值
λ
i
\lambda_{i}
λi,而
Q
Q
Q中的每一个列向量都是对应的特征值所对应的特征向量。
上述式子就是对称矩阵的特征值分解。我们一般将特征值从大到小排列在对角矩阵中,即
λ
1
≤
λ
2
≤
.
.
.
≤
λ
n
\lambda_{1}\le \lambda_{2}\le ...\le \lambda_{n}
λ1≤λ2≤...≤λn,所以
λ
1
(
A
)
=
λ
m
a
x
(
A
)
\lambda_{1}(A)=\lambda_{max}(A)
λ1(A)=λmax(A)。
对于特征值,还有些结论:
d
e
t
(
A
)
=
∏
i
=
1
n
λ
i
,
t
r
(
A
)
=
∑
i
=
1
n
λ
i
det(A)=\prod_{i=1}^{n}\lambda_{i},tr(A)=\sum_{i=1}^{n}\lambda_{i}
det(A)=i=1∏nλi,tr(A)=i=1∑nλi
Definiteness and Matrix inequalities
(前提仍然是对称矩阵,及表示成
S
n
S^{n}
Sn)
最大的特征值和最小的特征值分别满足:
λ
m
a
x
=
sup
x
≠
0
(
x
T
A
x
x
T
x
)
,
λ
m
i
n
=
inf
x
≠
0
(
x
T
A
x
x
T
x
)
\lambda_{max}=\underset{x\neq0}{\sup}(\frac{x^{T}Ax}{x^{T}x}),\lambda_{min}=\underset{x\neq0}{\inf}(\frac{x^{T}Ax}{x^{T}x})
λmax=x̸=0sup(xTxxTAx),λmin=x̸=0inf(xTxxTAx).
如果一个矩阵
A
∈
S
n
A\in S^{n}
A∈Sn并且满足
x
T
A
x
>
0
x^{T}Ax>0
xTAx>0,那么这个矩阵是正定的,记作
A
>
0
A>0
A>0(此处应是正定比较符号,但是没敲出来,哈哈哈),当且仅当所有特征值都大于0时成立,也即
λ
m
i
n
>
0
\lambda_{min}>0
λmin>0。反之,即负定。我们用
S
+
+
n
S^{n}_{++}
S++n描述在集合
S
n
S^{n}
Sn中的正定矩阵集合。如果含等号,那就是半正定或半负定。
对称平方根
若矩阵
A
∈
S
+
+
n
A\in S^{n}_{++}
A∈S++n,则
A
=
Q
Λ
Q
T
A=Q\Lambda Q^{T}
A=QΛQT,由于是正定的,所以特征值均大于,因此
A
=
A
1
2
A
1
2
,
A
1
2
=
Q
Λ
1
2
Q
T
A=A^{\frac{1}{2}}A^{\frac{1}{2}},A^{\frac{1}{2}}=Q\Lambda^{\frac{1}{2}}Q^{T}
A=A21A21,A21=QΛ21QT。
3、广义特征值分解


4、奇异值分解

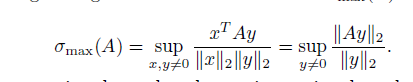
奇异矩阵的伪逆












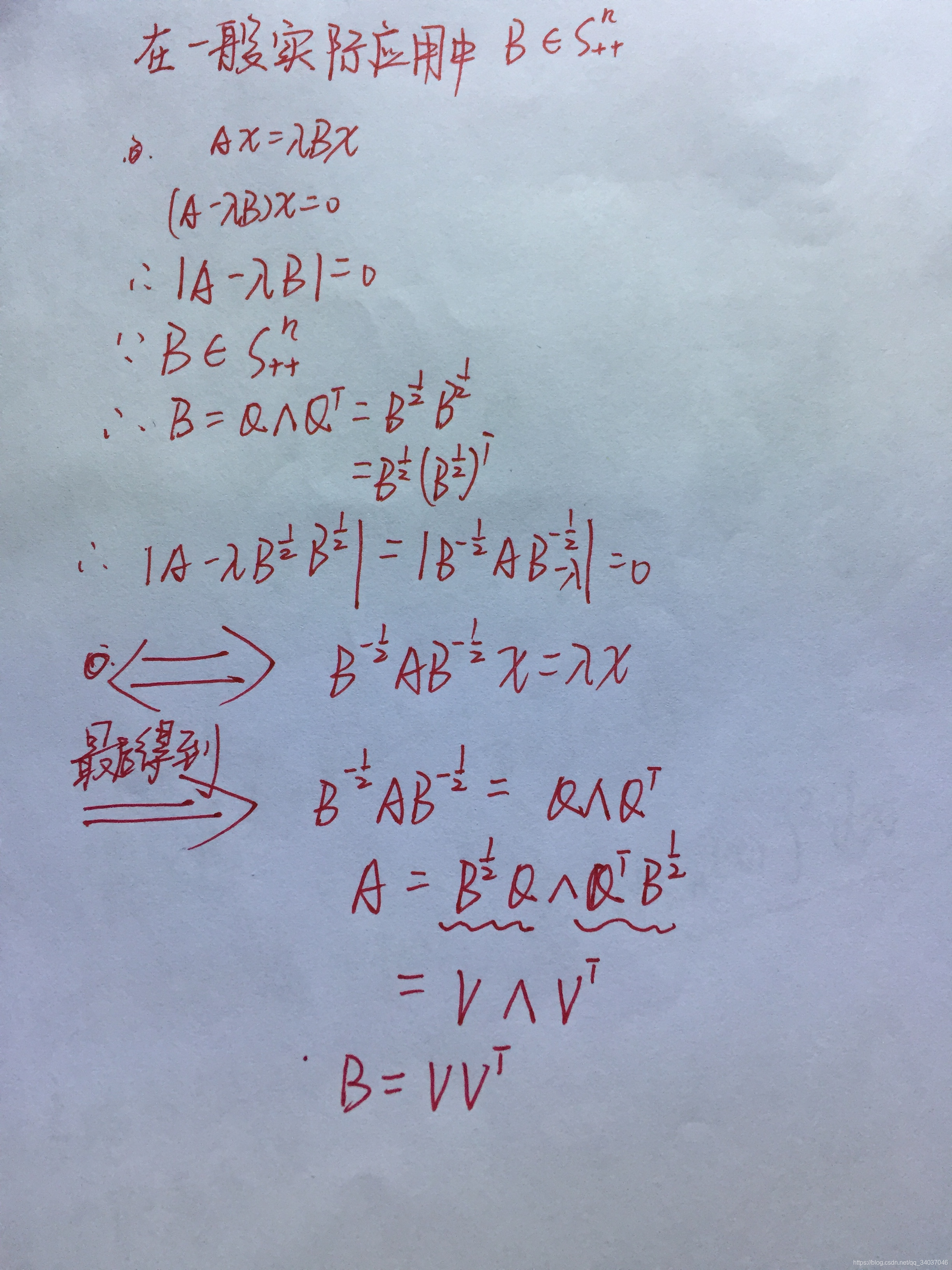














 11万+
11万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








