02 ，向量空间 ：序偶，运算，群，向量，n 维向量，列向量，行向量，向量空间，n 维空间

1 ，序偶 ：

1. 定义 ：有序二元组 ： (x,y)
2. 解释 ： 按照一定规则，计算 x,y
   x:序偶的第一元素
   y:序偶的第二元素

2 ，集合上的运算 ：

1. 定义 ：集合中的的一个序偶 (x,y) 的结果为集合中的第三个元素，成为集合中的运算
2. 集合 ：S = {1,2,3,4,5}
3. 例如 ： 2 + 3 = 5
4. 注意 ： 2,3,5 都属于 S 集合

3 ，群 ： 集合 + 运算

1. 定义 ：
   群 G = ( 集合 G ) + ( G 上的一个运算 )
2. 群需要满足三个条件 ：

0 ，* 代表一种运算，注意，不代表乘法，他现在暂时代表任意运算
1 ，结合性 ： 对于任意的 x,y,z ∈ G ，满足 x*(y*z) = (x*y)*z
2 ，中性元的存在性 ： 有一个 e∈G，满足 e*x = x*e = x
3 ，逆元存在 ： a*b=b*a=e

4 ，向量，n 维向量 ：

1. 定义 ：指具有大小和方向的量
2. n 维向量 ： n 个有次序的数称为 n 维向量

5 ，列向量，行向量 ： 一样的

1. 本质 ： 行向量与列向量没有本质的区别只是表现形式不同
2. 标识 ：列向量
   
3. 标识 ：行向量
   
4. 是否一样 ： 一样

6 ，向量空间 ： 定义

1. n 维向量 ： aT = {a1,a2,a3…an}
2. V 为 n 维向量的集合 ： 一堆的 n 维向量
   V = {aT1,aT2,aT3 … aTn}
3. 两种运算封闭 ：且向量 V 对于向量的加法和数乘两种运算封闭
4. 那么 ： 就称集合 V 为向量空间
5. 注意 ：
   加法封闭 ：
   
   数乘封闭 ：
   

7 ，向量空间 ： 表示

1. 向量空间 ：
   (V,+,R)

8 ，n 维实数空间 ：

(Rn,+,R)

9 ，三维空间 ：

1. (R3,+,R)
2. 手写是这样的 ：
   
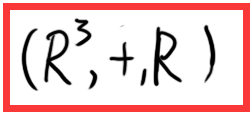
3. 他的运算是这样的 ：
   

10 ，向量空间 ： 个人理解

1. 他是加法空间
2. 无限大的空间
3. 可以按照乘法，无限扩展