Zhu and 772002
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 1800 Accepted Submission(s): 625
But 772002 has a appointment with his girl friend. So 772002 gives this problem to you.
There are n numbers a1,a2,...,an . The value of the prime factors of each number does not exceed 2000 , you can choose at least one number and multiply them, then you can get a number b .
How many different ways of choices can make b is a perfect square number. The answer maybe too large, so you should output the answer modulo by 1000000007 .
For each test case:
First line includes a number n(1≤n≤300) ,next line there are n numbers a1,a2,...,an,(1≤ai≤1018) .
Then output the answer of i-th test case modulo by 1000000007 .
2 3 3 3 4 3 2 2 2
Case #1: 3 Case #2: 3
题意:给你n个数字,它们的质因数不超过2000,问从n个数中至少选取1个数,它们的乘积是完全平方数的情况有多少种,结果对1000000007取模。
思路:
训练指南原题改编,P160。下为书上讲解:
“不含大于2000的素因子”提示我们考虑每个数的唯一分解式,用01向量表示—个数, 再用n个01变量
xi
来表示我们的选择,其中
xi=1
表示要选第i个数,
xi=0
表示不选它,则可对每个素数的幂列出一个模2的方程。
这话听起来比较抽象,让我们分析一下题目中的例子。4个整数4,6,10,15的素因子只 有2, 3, 5这3种,首先把这些整数写成01向量的的形式,即
4=22∗30∗50
,即(2,0,0);
6=21∗31∗50
,即(1,1,0);
10=21∗30∗51
,即(1,0,1);
15=20∗31∗51
,即(0,1,1)。
选出来的数乘积为
22x1+x2+x3∗3x2+x4∗5x3+x4
。如果要让这个数是完全平方数,每个幂都应该是偶数,即
注意,这也是一个线性方程组,只是代数系统变成了 Z2 (模2的剩余系)。可是第一 个方程里的2 x1 不见了。这是因为2 x1 总是偶数,所以没必要写在方程里。同理,3 x1 会变成 x1 ,任意变量的系数非0即1。还可以把这个方程组看成是如下xor方程组
需要求解方程组解的组数。可以求秩,即求到自由变元的个数。xor方程组是很好消元的,因为不需要做乘法和除法,只需要做xor;每次也不需要找 绝对值最大的系数(每个系数不是0就是1),任意一个系数为1即可实现消元。
最后,假设自由变量有f个,则线性方程组的解共有 2f 个,因为每个自由变量可以取0和1。比如,刚才的方程组对应的增广矩阵消元后为
有两个自由变量 x1 和 x4 ,有两个有界变量 x2 和 x3 ,因此—共有 22 =4种选法。注意,本题不允许一个整数都不选,因此最终答案需要减1。
换句话说,我们需要做的就是对给的数做素数分解,因为素数大小不超过2000,2000以内素数有303个,所以开个二维数组,记录每个题给数的素数因子个数,个数偶数记为0,奇数记为1(素数分解时不断异或1就行了)。得到二维数组实际就是系数矩阵。求矩阵的秩就可以。高斯消元的模板。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <stack>
#include <iomanip>
#include <string>
using namespace std;
const int MAXN=305;
const int oo=1000000007;
typedef int Matrix[2107][2107];
typedef long long LL;
Matrix A;
int ra_nk(int m,int n)//A是异或方程组系数矩阵 返回秩
{
int i=0,j=0,k,r,u;
while(i<m&&j<n)
{
r=i;
for(int k=i;k<m;k++)
{
if(A[k][j]) { r=k;break; }
}
if(A[r][j])
{
if(r!=i) for(k=0;k<=n;k++) swap(A[r][k],A[i][k]);
//消元后第i行的第一个非0列是第j列,且第u>i行的第j列均为0
for(u=i+1;u<m;u++) if(A[u][j])
for(k=i;k<=n;k++) A[u][k]^=A[i][k];
i++;
}
j++;
}
return i;
}
int vis[2107];
int prime[2107];
int gen_primes(int m)
{
memset(vis,0,sizeof(vis));
int cnt=0;
for(int i=2; i < m; i++)
{
if(!vis[i])
{
prime[cnt++]=i;
for(int j=i*i; j<m; j+=i)
vis[j]=1;
}
}
return cnt;
}
LL powmod(LL a,LL n)
{
LL mod=1e9+7;
LL res=1;
while(n){
if(n&1) res=res*a%mod;
a=a*a%mod;
n>>=1;
}
return res;
}
int main()
{
int prime_n=gen_primes(2107);
int T;
scanf("%d",&T);
for(int t=1;t<=T;t++)
{
memset(A,0,sizeof(A));
int n;
scanf("%d",&n);
int maxp=0;
for(int i=0;i<n;i++)
{
LL x;
scanf("%lld",&x);
for(int j=0;j<prime_n;j++)
{
while(x%prime[j]==0)
{
maxp=max(maxp,j);
x/=prime[j];
A[j][i]^=1;
}
}
}
int r=ra_nk(maxp+1,n);
printf("Case #%d:\n",t);
printf("%lld\n",powmod(2,(LL)n-r)-1);
}
}转载的一个解释:
首先,我们知道的是,完全平方数的各种质因子必定出现偶数次
不然不可能被开方
例如36=2*2*3*3
质因子2,3均出现两次
所以呢,此题已经可以转化为类似开关问题的高斯消元了
这里,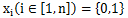
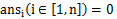
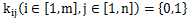
剩下的就是套一下高斯消元的模板,求解出自由变元的个数ans,那此题的结果就是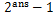
如果还是不明白的话,我们来举例说明
就比如样例3,3,4
方程变元x前的系数k为我们打素数表2,3,5,……,1999中第k个质数出现奇数次还是偶数次
那该样例可得方程组为
第一条方程是质数2的贡献,因为3是不包含质因子2的,故贡献为0,而4虽包含质因子2,但出现了偶数次,故贡献同样为0
第二条方程,两个3都贡献了1,而4不包含质因子3,所以无贡献
显然,方程组只有一条方程,但有3个未知数,所以自由变元有2个,而自由变元的取值为{0,1}
故方程组的解有2^2=4种,除去全为0的一种(因为题目指明至少取一个数),剩3种(1,1,0),(0,0,1),(1,1,1)
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 305;
const int M = 2001;
const int inf = 1000000007;
const int mod = 1000000007;
int prime[M],k;
bool v[M];
//有equ个方程,var个变元。增广矩阵行数为equ,列数为var+1,分别为0到var
int equ,var;
int a[N][N]; //增广矩阵
int x[N]; //解集
int free_x[N];//用来存储自由变元(多解枚举自由变元可以使用)
int free_num;//自由变元的个数
void get_prime()
{
k=0;
for(int i=2;i<M;i++)
if(!v[i])
{
prime[k++]=i;
for(int j=i;j<M;j+=i)
v[j]=true;
}
}
__int64 Quick_Mod(int a,int b)//快速幂
{
__int64 res = 1,term = a % mod;
while(b)
{
if(b & 1) res = (res * term) % mod;
term = (term * term) % mod;
b >>= 1;
}
return res;
}
//返回值为-1表示无解,为0是唯一解,否则返回自由变元个数
int Gauss()
{
int max_r,col,k;
free_num = 0;
for(k = 0, col = 0 ; k < equ && col < var ; k++, col++)
{
max_r = k;
for(int i = k+1;i < equ;i++)
{
if(abs(a[i][col]) > abs(a[max_r][col]))
max_r = i;
}
if(a[max_r][col] == 0)
{
k--;
free_x[free_num++] = col;//这个是自由变元
continue;
}
if(max_r != k)
{
for(int j = col; j < var+1; j++)
swap(a[k][j],a[max_r][j]);
}
for(int i = k+1;i < equ;i++)
{
if(a[i][col] != 0)
{
for(int j = col;j < var+1;j++)
a[i][j] ^= a[k][j];
}
}
}
for(int i = k;i < equ;i++)
if(a[i][col] != 0)
return -1;//无解
if(k < var) return var-k;//自由变元个数
//唯一解,回代
for(int i = var-1; i >= 0;i--)
{
x[i] = a[i][var];
for(int j = i+1;j < var;j++)
x[i] ^= (a[i][j] && x[j]);
}
return 0;
}
int main()
{
get_prime();
int t,i,j,n,p=1,c;
__int64 ans,s;
scanf("%d",&t);
while(t--)
{
ans=0;
memset(a,0,sizeof(a));
scanf("%d",&n);
equ=k;var=n;
for(i=0;i<n;i++)
{
scanf("%I64d",&s);
for(j=0;j<k;j++)
{
c=0;
while(s%prime[j]==0)
{
s/=prime[j];
c++;
}
if(c&1)
a[j][i]=1;
}
}
int r,c;
ans=Gauss();
printf("Case #%d:\n%I64d\n",p++,Quick_Mod(2,ans)-1);
}
return 0;
} 










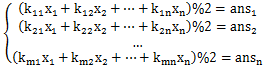
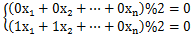















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








