插值操作interp(MATLAB&python版）

插值操作

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其它点处的近似值。
插值可以实现对数据的平滑，或对缺失间断等部分的补偿。
与拟合不同的是，插值要求曲线通过所有的已知数据。计算插值有两种基本的方法：

• 对一个完整的数据集去拟合一个函数；
• 仿样内插法：对数据集的不同部分拟合出不同的函数，而函数之间的曲线平滑对接。

MATLAB插值函数interp1

参考链接：interp1

插值法又称“内插法”，是利用函数f (x)在某区间中已知的若干点的函数值，作出适当的特定函数，在区间的其他点上用这特定函数的值作为函数f (x)的近似值，这种方法称为插值法。如果这特定函数是多项式，就称它为插值多项式。
函数使用基本形式：

yq = interp1(x, y, xq, method, extrapolation)

• x和y为已知输入样本；
• xq为需要预测的自变量序列，yq为相对应预测的变量序列；
• method为插值方法，包括’linear’、‘nearest’、‘next’、‘previous’、‘pchip’、‘cubic’、‘v5cubic’、‘makima’ 或 ‘spline’。默认方法为 ‘linear’；
• extrapolation为外插相关设置。来计算落在 x 域范围外的点。如果希望使用 method 算法进行外插，可将 extrapolation 设置为 ‘extrap’。您也可以指定一个标量值，这种情况下，interp1 将为所有落在 x 域范围外的点返回该标量值。

注意：所有的插值方法都要求x是单调的，并且xi不能够超过x的范围。

举例1：

%{
    例如：在一 天24小时内，从零点开始每间隔2小时测得的环境温度数据分别为
            12，9，9，1，0，18 ，24，28，27，25，20，18，15，13，
    推测中午12点（即13点）时的温度．
%}
x = 0:2:24;
y = [12   9   9   10   18  24   28   27   25   20  18  15  13];
a = 13;
y1 = interp1(x,y,a,'spline')
% 结果为：  27.8725

% 若要得到一天24小时的温度曲线，则：
xi = 0:1/3600:24;
% 插值点可以是向量，则返回的也就是对应的向量
yi = interp1(x,y,xi, 'spline');
plot(x,y,'o' ,xi,yi);

结果：

举例2：基于粗略采样的正弦函数进行插值

clear
clc

x = 0:pi/4:2*pi;%一个正弦函数
y = sin(x);
xq = 0:pi/10:2*pi;%将查询点定义为 x 范围内更精细的采样点。

figure
yq1 = interp1(x,y,xq); % 线性
yq2 = interp1(x,y,xq,'nearest'); % 邻近
yq3 = interp1(x,y,xq,'spline'); % 三次样条

subplot(3,1,1);
plot(x,y,'ro',xq,yq1,'r-*','LineWidth',1);
xlim([0 2*pi]);
subplot(3,1,2);
plot(x,y,'ro',xq,yq2,'r-*','LineWidth',1);
xlim([0 2*pi]);
subplot(3,1,3);
plot(x,y,'ro',xq,yq3,'r-*','LineWidth',1);
xlim([0 2*pi]);

结果：

举例3：在不指定样本点的情况下进行插值

v = [0  1.41  2  1.41  0  -1.41  -2  -1.41 0];%定义一组函数值。
xq = 1.5:8.5;%定义一组介于默认点 1:9 之间的查询点。在这种情况下，默认点为 1:9，因为 v 包含 9 个值。
vq = interp1(v,xq);%计算 xq 处的 v

figure
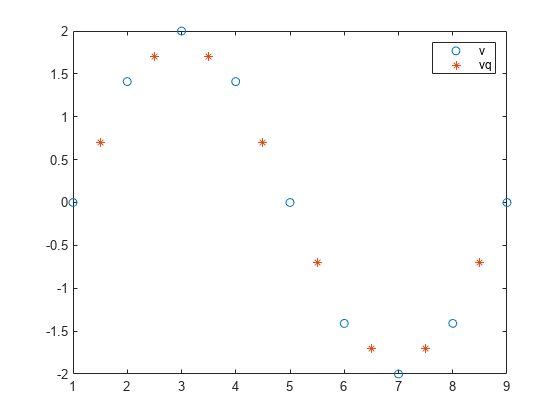
plot((1:9),v,'o',xq,vq,'*');
legend('v','vq');

结果:

举例4：使用两种不同方法进行外插

x = [1 2 3 4 5];
v = [12 16 31 10 6];

xq = [0 0.5 1.5 5.5 6 8 10];%指定查询点 xq，这些查询点延伸到 x 的定义域以外。
vq1 = interp1(x,v,xq,'pchip');
vq2 = interp1(x,v,xq,'linear');
vq3 = interp1(x,v,xq,'linear','extrap');

结果：

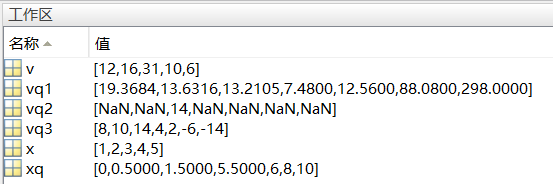
‘pchip’ 默认外插，但 ‘linear’ 不会。

举例5：

x = 0:2*pi;  
y = sin(x);  
xx = 0:0.5:2*pi;  

% interp1对sin函数进行分段线性插值，调用interp1的时候，默认的是分段线性插值  
y1 = interp1(x,y,xx,'linear');  
subplot(2,2,1);
plot(x,y,'o',xx,y1,'r')  
title('分段线性插值')  
  
% 临近插值  
y2 = interp1(x,y,xx,'nearest');  
subplot(2,2,2);
plot(x,y,'o',xx,y2,'r');  
title('临近插值')  
  
%球面线性插值  
y3 = interp1(x,y,xx,'spline');  
subplot(2,2,3);
plot(x,y,'o',xx,y3,'r')  
title('球面插值')  
  
%三次多项式插值法  
y4 = interp1(x,y,xx,'pchip');  
subplot(2,2,4);
plot(x,y,'o',xx,y4,'r');  
title('三次多项式插值')  

结果：

python插值方法

我们一般用scipy库，里面的scipy.interpolate是插值模块。
SciPy的interpolate模块提供了许多对数据进行插值运算的函数，范围涵盖简单的一维插值到复杂多维插值求解。

当样本数据变化归因于一个独立的变量时，就使用一维插值；反之样本数据归因于多个独立变量时，使用多维插值。

这里简单介绍一维数据的插值。

内插值 interp1d()：
一维数据的插值运算可以通过函数interp1d()完成。其调用形式如下，它实际上不是函数而是一个类：

interp1d(x, y, kind='linear', ...)

其中，x和y参数是一系列已知的数据点，kind参数是插值类型，可以是字符串或整数，它给出插值的B样条曲线的阶数，候选值及作用下表所示：

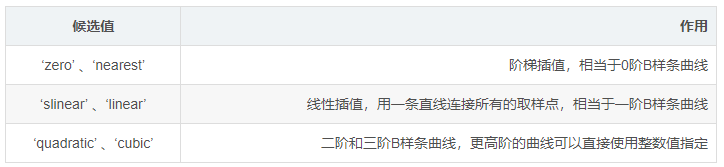
interp1d比Matlab的interp有些优势，因为返回的是函数，不需要在事先设定需要求解的点，而是在需要使用时调用函数。

import numpy as np
from scipy import interpolate
from matplotlib import pyplot as plt

x=np.linspace(0,10,5)
y=np.sin(x)
xnew=np.linspace(0,10,101)
plt.plot(x,y,'ro', label="interpolating point")
list1=['linear','nearest']

for kind in list1:
    f=interpolate.interp1d(x,y,kind=kind)
    #f是一个函数，用这个函数就可以找插值点的函数值了：
    ynew=f(xnew)
    plt.plot(xnew,ynew,label=kind)
plt.plot(xnew,np.sin(xnew),label="real f(x)",linestyle="--")
plt.legend(loc='lower right')
plt.show()

结果：

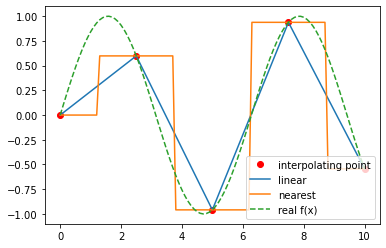
外插值：
可以使用UnivariateSpline进行外插值。
调用方式如下：

UnivariateSpline(x,y,w=None,bbox=[None,None],k=3,s=None)

x,y是X-Y坐标数组
w是每个数据点的权重值
k为样条曲线的阶数
s为平滑参数（s=0，样条曲线强制通过所有插值点）

x1=np.linspace(0,10,20)
y1=np.sin(x1)

sx1=np.linspace(0,15,100)
func1=interpolate.UnivariateSpline(x1,y1,s=0)
sy1=func1(sx1)
plt.plot(x1,y1,'o', label="interpolation points")
plt.plot(sx1,sy1, label="interpolation function")
plt.plot(sx1,np.sin(sx1), label="real function")
plt.legend()
plt.show()

结果：

我们可以发现，在插值区间 [0,10] 之间，interpolation function 和 real function极为接近，但是一旦超出该区间，即外插值，插值的效果就会非常差。