二维随机变量的条件分布:
定义:
在两个随机变量 X,Y的情况下,给定Y 取某些值的情况下, 称: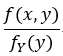 是Y =y 的条件下X的条件概率密度;
是Y =y 的条件下X的条件概率密度;
离散型随机变量的条件分布:
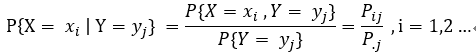 为在 Y =
为在 Y = ![]() 条件下随机变量 f(x,y) 的条件分布律;
条件下随机变量 f(x,y) 的条件分布律;
即 离散型随机变量的条件分布 = 联合分布 概率 / 边缘分布 概率(注意,可能会用到级数);
连续型随机变量的条件分布:
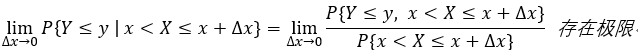 称 它为 极限 X= x的条件下,y的条件分布函数; 记为: P{Y<= y | X = x} 或者:
称 它为 极限 X= x的条件下,y的条件分布函数; 记为: P{Y<= y | X = x} 或者:![]() 且有:
且有: 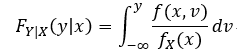 即: 对条件概率密度 积分 可求得 条件分布;
即: 对条件概率密度 积分 可求得 条件分布;
联合分布 可求 边缘分布 以及条件分布; 边缘分布 与 条件分布 也可求 联合分布;
相互独立的随机变量:
判定: 1. 变量间互不影响(离散型);
2. 它们的两个边缘分布 概率的乘积 等于联合分布 概率(连续型);
即 对连续性随机变量,若: ![]() 成立,则 这两个随机变量相互独立;
成立,则 这两个随机变量相互独立;
数学期望:
理解: 即 加权平均, 也即: 随机变量可能取到的值与其概率之积 的累加;
离散型随机变量的数学期望:
设 X 分布律 为: ![]()
若 级数: 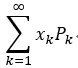 绝对收敛,则 称 级数
绝对收敛,则 称 级数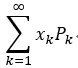 的和 为 随机变量X 的数学期望,记为: E(X);
的和 为 随机变量X 的数学期望,记为: E(X);
E(x) =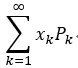
连续型随机变量的数学期望:
设连续型随机变量 X 的概率密度 为 f(x) , 若积分 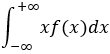 绝对收敛,则称 积分
绝对收敛,则称 积分 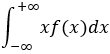 为X 的数学期望,记为:E(X);
为X 的数学期望,记为:E(X);
E(x) =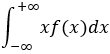
常见随机变量的数学期望:
指数分布: ![]() 方差:
方差:![]() 数学期望:θ;
数学期望:θ;
均匀分布: ![]() 方差:
方差: 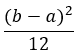 数学期望:
数学期望: ![]()
二项分布: ![]() 方差: np(1-p) 数学期望: np
方差: np(1-p) 数学期望: np
泊松分布: 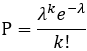 方差: λ 数学期望:λ
方差: λ 数学期望:λ
正态分布: 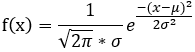 方差: σ^2 数学期望: μ
方差: σ^2 数学期望: μ
数学期望的性质:
1. E(C) =c;
2. E(2C) = 2E(C);
3. E(X+Y) = E(X)+E(Y);
4. 若 X与 Y 相互独立,则E(X*Y) = E(X)E(Y);
二维随机变量的数学期望:
E(XY) =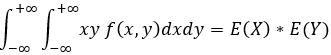
随机变量的函数 的数学期望:
离散型: 概率(权值)不变,相应的随机量变化;
连续型: E( g(x) ) = 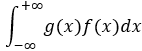 (大写变小写)
(大写变小写)
随机变量的方差:
常用来体现随机变量取值 分散程度的量;
定义:
若X 是 一个随机变量,有: ![]() 存在,称:
存在,称: ![]() 为 X 的方差,记为 D(X);
为 X 的方差,记为 D(X);
D(X) = E(X^2) - E^2(X), 即:方差 等于 随机变量的平方 的期望 - 随机变量的期望 的平方;
![]() 为标准差 或 均方差,记为 :σ(X);
为标准差 或 均方差,记为 :σ(X);
离散型随机变量的方差计算:
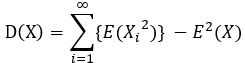
连续型随机变量的方差计算:
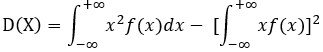
或者: 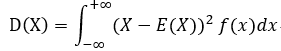
性质:
1. D(C)=0; C 为常数;
2. 若X,Y相互独立, 则: D(X+- Y) = D(X) +- D(Y);
3. D(CX) =C^2 * D(X);
4. D(aX+b) = a^2 * D(X);
5. D(-X) = D(X);
标准化变量: 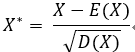 的期望为 0, 方差为 1;
的期望为 0, 方差为 1;
切比雪夫不等式:
若随机变量 X 具有 E(X) = μ, 方差 D(X) = σ^2 , 则 对于任意 ε, 有不等式:
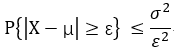
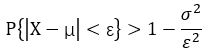
协方差:
定义:
Cov(X,Y) = E[ ( X-E(X) )*(Y-E(Y) ) ] ;
计算公式:
若 X,Y 相互独立, Cov(X,Y) = E[ X-E(X)] * E[Y-E(Y)] =0;
Cov(X,Y) = E(XY) - E(X)E(Y);
D(X+Y) = D(X) + D(Y) + 2 Cov(X,Y);
D(X-Y) = D(X) + D(Y) - 2 Cov(X,Y);
性质:
Cov(X,Y) = Cov(Y,X);
Cov(aX,bY) = ab Cov(X,Y);
Cov(X1+X2,Y) = Cov(X1,Y) + Cov(X2,Y);
若 X,Y相互独立,则 E(X,Y) = E(X)*E(Y);
相关系数:
定义:
设 (X,Y) 为 二维随机变量, D(X),D(Y) Cov(X,Y) 满足: 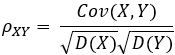 , 称
, 称 ![]() 为相关系数, 它反映了 X与 Y 相关关系的无量纲的关系;
为相关系数, 它反映了 X与 Y 相关关系的无量纲的关系;
当 ![]() =0 时, X 与 Y 不相关;
=0 时, X 与 Y 不相关;
注意: 相互独立 ==> ρ=0; ρ=0 =/=>相互独立;
性质:
-1 <= ![]() <= 1;
<= 1;
| ![]() | =1 的充要条件: 存在 a,b ,使得 P(Y = a+bX) =1,即 X与 Y 几乎处处有线性关系;
| =1 的充要条件: 存在 a,b ,使得 P(Y = a+bX) =1,即 X与 Y 几乎处处有线性关系;
![]() >0 称为 正相关;
>0 称为 正相关; ![]() <0 称为 负相关;
<0 称为 负相关;
当![]() =1时,线性关系最强;
=1时,线性关系最强;
大数定理:
伯努利大数定理: 包含 切比雪夫弱大数定理; 辛钦弱大数定理;
概率是频率的稳定值;
抛硬币实验的数学意义:
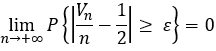
它表示 频率不一定 为 1/2, 但与 1/2 的偏差 >= ε的概率为0;
切比雪夫弱大数定理:
设 x1,x2 ... 为独立随机变量序列,它们具有共同的数学期望μ, 并且 D(xi) <= C, i=1,2 ...
且 对任意的 ε >0 , 有 D(xi):
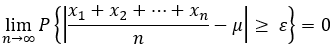
辛钦弱大数定理:
设 x1,x2 ... 相互独立,服从同一分布, 具有数学期望: E(xi) = μ,i=1,2, ... , 且 对任意的 ε >0, 有:
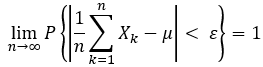
中心极限定理:
作用: 用于研究正态分布; 用于研究 独立的随机变量;
定义:
把 随机变量的和 的分布 收敛于 正态分布 这一类 定理 称为 中心极限定理;
求和的标准化公式: 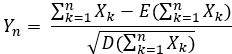
定理一:
随机变量序列 独立 且服从同一分布时, 有:
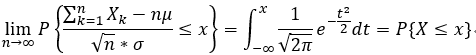
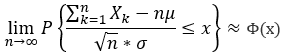 : 求概率的方法
: 求概率的方法
定理二(德莫佛-拉普拉斯方程):
设随机变量 ![]() (n=1,2,...) 服从参数为 n,p的二项分布, 则对于任意x ,恒有:
(n=1,2,...) 服从参数为 n,p的二项分布, 则对于任意x ,恒有:
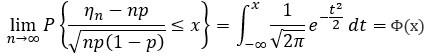
它的修正方程:
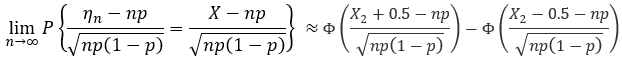





 本文深入探讨了随机变量的概念,包括二维随机变量的条件分布、数学期望、方差、协方差、相关系数等关键统计量的定义及计算方法。同时,介绍了大数定律与中心极限定理在统计学中的应用。
本文深入探讨了随机变量的概念,包括二维随机变量的条件分布、数学期望、方差、协方差、相关系数等关键统计量的定义及计算方法。同时,介绍了大数定律与中心极限定理在统计学中的应用。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








