棋盘覆盖问题

分治法——棋盘覆盖问题

文章是我转载的，源地址为http://blog.csdn.net/q547550831/article/details/51541527

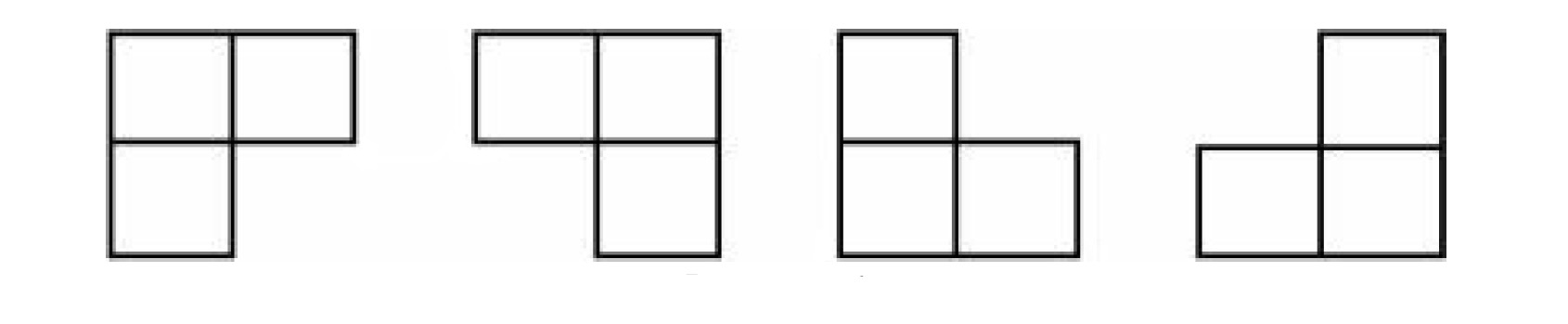
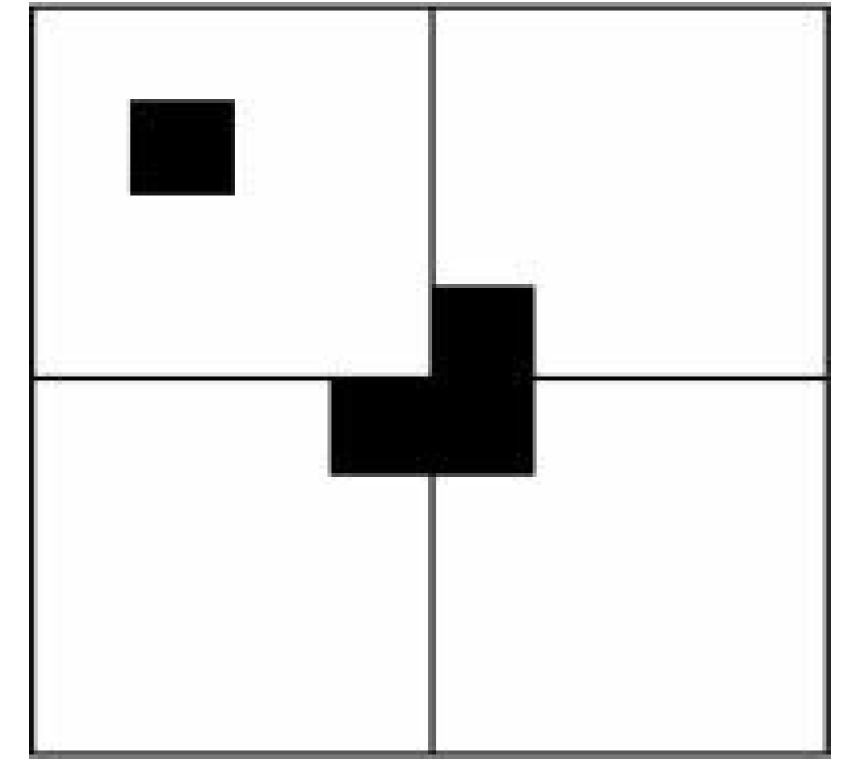
棋盘覆盖问题。有一个 2k∗2k 的方格棋盘，恰有一个方格是黑色的，其他为白色。你的任务是用包含3个方格的L型牌覆盖所有白色方格。黑色方格不能被覆盖，且任意一个白色方格不能同时被两个或更多牌覆盖。如图所示为L型牌的4种旋转方式。

分治三步骤

划分问题：将 2k∗2k 的棋盘划分为 2k−1∗2k−1 这样的子棋盘4块。

递归求解：递归填充各个格子，填充分为四个情况，在下面会有解释，递归出口为 k=0 也就是子棋盘方格数为1。

合并问题：不需要合并子问题。

递归填充的四种情况

如果黑方块在左上子棋盘，则递归填充左上子棋盘；否则填充左上子棋盘的右下角，将右下角看做黑色方块，然后递归填充左上子棋盘。

如果黑方块在右上子棋盘，则递归填充右上子棋盘；否则填充右上子棋盘的左下角，将左下角看做黑色方块，然后递归填充右上子棋盘。

如果黑方块在左下子棋盘，则递归填充左下子棋盘；否则填充左下子棋盘的右上角，将右上角看做黑色方块，然后递归填充左下子棋盘。

如果黑方块在右下子棋盘，则递归填充右下子棋盘；否则填充右下子棋盘的右下角，将左上角看做黑色方块，然后递归填充右下子棋盘。

棋盘覆盖问题分治算法

void chessBoard(int row, int column, int x, int y, int siz) {
    // 递归出口
    if(siz == 1) {
        return;
    }

    // 对半划分成2^(siz - 1) * 2^(siz - 1)的棋盘
    int s = siz / 2;
    // L型牌编号自增
    int t = ++number;
    // 中间点，以此判别(x,y)在哪个子棋盘中
    int centerRow = row + s;
    int centerColumn = column + s;
    // 黑色方格在左上子棋盘
    if(x < centerRow && y < centerColumn) {
        chessBoard(row, column, x, y, s);
    } else {
        // 不在则填充左上子棋盘的右下角
        chess[centerRow - 1][centerColumn - 1] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(row, column, centerRow - 1, centerColumn - 1, s);
    }

    // 黑色方格在右上子棋盘
    if(x < centerRow && y >= centerColumn) {
        chessBoard(row, centerColumn, x, y, s);
    } else {
        // 不在则填充右上子棋盘的左下角
        chess[centerRow - 1][centerColumn] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(row, centerColumn, centerRow - 1, centerColumn, s);
    }

    // 黑色方格在左下子棋盘
    if(x >= centerRow && y < centerColumn) {
        chessBoard(centerRow, column, x, y, s);
    } else {
        // 不在则填充左下子棋盘的右上角
        chess[centerRow][centerColumn - 1] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(centerRow, column, centerRow, centerColumn - 1, s);
    }

    // 黑色方格在右下子棋盘
    if(x >= centerRow && y >= centerColumn) {
        chessBoard(centerRow, centerColumn, x, y, s);
    } else {
        // 不在则填充右下子棋盘的左上角
        chess[centerRow][centerColumn] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(centerRow, centerColumn, centerRow, centerColumn, s);
    }

测试主程序

#include <iostream>

using namespace std;

const int maxNum = 1 << 10;
// 棋盘
int chess[maxNum][maxNum];
// L型牌编号
int number;

void chessBoard(int row, int column, int x, int y, int siz) {
    // 递归出口
    if(siz == 1) {
        return;
    }

    // 对半划分成2^(siz - 1) * 2^(siz - 1)的棋盘
    int s = siz / 2;
    // L型牌编号自增
    int t = ++number;
    // 中间点，以此判别(x,y)在哪个子棋盘中
    int centerRow = row + s;
    int centerColumn = column + s;
    // 黑色方格在左上子棋盘
    if(x < centerRow && y < centerColumn) {
        chessBoard(row, column, x, y, s);
    } else {
        // 不在则填充左上子棋盘的右下角
        chess[centerRow - 1][centerColumn - 1] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(row, column, centerRow - 1, centerColumn - 1, s);
    }

    // 黑色方格在右上子棋盘
    if(x < centerRow && y >= centerColumn) {
        chessBoard(row, centerColumn, x, y, s);
    } else {
        // 不在则填充右上子棋盘的左下角
        chess[centerRow - 1][centerColumn] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(row, centerColumn, centerRow - 1, centerColumn, s);
    }

    // 黑色方格在左下子棋盘
    if(x >= centerRow && y < centerColumn) {
        chessBoard(centerRow, column, x, y, s);
    } else {
        // 不在则填充左下子棋盘的右上角
        chess[centerRow][centerColumn - 1] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(centerRow, column, centerRow, centerColumn - 1, s);
    }

    // 黑色方格在右下子棋盘
    if(x >= centerRow && y >= centerColumn) {
        chessBoard(centerRow, centerColumn, x, y, s);
    } else {
        // 不在则填充右下子棋盘的左上角
        chess[centerRow][centerColumn] = t;
        // 然后覆盖其他格子，注意这时(x,y)要看做已填充位置
        chessBoard(centerRow, centerColumn, centerRow, centerColumn, s);
    }

}

int main() {
    // 大小，黑色方格位置
    int siz, x, y;
    while(true) {
        cout << "(x,y)从(0,0)开始,输入数据为0 0 0即结束程序。" << endl;
        cout << "请输入棋盘大小和黑色方格位置(x,y)：";
        cin >> siz >> x >> y;
        // 退出条件
        if(siz == 0) {
            break;
        }
        // 涂黑(x,y)，初始化L型牌编号
        chess[x][y] = number = 1;

        // 分治法填满棋盘
        chessBoard(0, 0, x, y, siz);

        // 输出该棋盘
        for(int i = 0; i < siz; i++) {
            for(int j = 0; j < siz; j++) {
                cout << chess[i][j] << "\t";
            }
            cout << endl << endl << endl;
        }
    }

    return 0;
}

输出数据

(x,y)从(0,0)开始,输入数据为0 0 0即结束程序。
请输入棋盘大小和黑色方格位置(x,y)：2 0 0
1       2


2       2


(x,y)从(0,0)开始,输入数据为0 0 0即结束程序。
请输入棋盘大小和黑色方格位置(x,y)：4 1 1
3       3       4       4


3       1       2       4


5       2       2       6


5       5       6       6


(x,y)从(0,0)开始,输入数据为0 0 0即结束程序。
请输入棋盘大小和黑色方格位置(x,y)：8 2 2
4       4       5       5       9       9       10      10


4       3       3       5       9       8       8       10


6       3       1       7       11      11      8       12


6       6       7       7       2       11      12      12


14      14      15      2       2       19      20      20


14      13      15      15      19      19      18      20


16      13      13      17      21      18      18      22


16      16      17      17      21      21      22      22



(x,y)从(0,0)开始,输入数据为0 0 0即结束程序。
请输入棋盘大小和黑色方格位置(x,y)：0 0 0

Process returned 0 (0x0)   execution time : 29.988 s
Press any key to continue.