数学小知识（长期更新)

###如果有任何地方写错了，欢迎在评论里指出

#前言
今天开始学习数论，大概就是学一些自己以前不会或者说搞得不是特别懂的东西。
原因
1.感觉以前学数论都是背了结论就跑，一直没有理解，感觉不仅容易忘，想起来还漏洞百出，特地来填一下坑。
2.感觉自己的数论太弱了，之前出了一个扩展欧拉定理都不会了QAQ
其实我就没会过
不管有用的没用的都学了一下,留个印象吧,至少可以装逼。
学习顺序大致是前面是后面的基础

#10.22下午
##整除的定义：
如果$n/m$是一个整数，且$m>0$，那么就是整除，注意要$m>0$

##欧几里得算法：
$\gcd (0,n)=n$
$\gcd (m,n)=\gcd (n\%m,m)$

##扩展欧几里得算法：
$m^{\prime }m+n^{\prime }n=\gcd (n,m)$
求可行的$m^{\prime }$和$n^{\prime }$
当$m=0$时,使得$m^{\prime }=0,n^{\prime }=1$
反之另$r=n\%m$
并用$r,m$递归操作
由于$r=n-\lfloor n/m\rfloor \ast m$，（前面的是下取整)且$r{r}^{\prime }+m{m}^{\prime }=\gcd (m,n)$
然后把$r$代过去就可以了

##算术基本定理
我才不会告诉你我没有认真看证明呢

##一些看似没什么用的定义：
欧几里得数和麦森数，麦森数质数

##阶乘的增长速度
$n^{n/2}<=n!<=\frac{(n+1{)}^n}{2^n}$
证明挺简单的，不写了

##斯特林公式
误差大概是1/(12n)，感觉没什么用。。

##求出n!含有多少个2，（不是2的类推）：
朴素算法大家都会，就是$$\sum _{i=1}^{\infty }\lfloor n/i\rfloor$$
然后log次久之后就都是0了
然后还有另外一种算法，定义$v(n)$为n的二进制中1的个数
然后答案就是$n-v(n)$
这个大家可以化成二进制，然后考虑每一位对答案的贡献，就可以得出那个式子了

##当然还有上面那个问题答案的上界
$ans<\frac{n}{p}+\frac{n}{p^2}+\frac{n}{p^3}+\frac{n}{p^4}+\frac{n}{p^k}$
k趋向与$\infty$
用等比数列可以将该式子化成$ans<\frac{n}{p-1}$
这个似乎也没什么用，但是我学了一下无穷几何级数求和

#10.22晚
（因为很困，所以效率极低）
##逆元
对于正整数$ax\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$
具体有什么用？当要对模数进行除法的时候可以改为乘他的逆元

原因(d为被除数）：
$\frac{d}{a}(modp)=\frac{d}{a}\ast a\ast x(modp)=d\ast x(modp)$

怎么求呢？
解不定方程（用欧几里得即可）：ax+bp=1
正确性显然

快速幂：$a^{(p-2)}$次方即为他的逆元
根据费马小定理:
$a^{(p-1)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$
$a\ast a^{(p-2)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}p)$
要值得除以的是，这个这个定理是当p为质数且a，p互质的时候成立的，所以实用性没那么广

存在条件：a与p互质
因为当且仅当a和q互质的时候，不定方程有解（原因看下一个）
费马小定理成立，且费马小定理还必须当p时质数

##裴蜀定理
内容:ax+by=d有解的条件为d是gcd(x,y)的倍数
设g=gcd(x,y)
ax+by=g的情况一定有解，我有一个不靠谱的想法：既然构造方式都有了，又怎么会无解呢？
又因为x是g的倍数，y是g的倍数，所以ax+by当然也是g的倍数啦
所以当g不为1的时候，ax+by=1是无解的，所以逆元要求a和q互质

##法里级数
定义：阶为N的法里级数，是介于0到1之间分母不超过N的所有最简分数组成的数的集合，且按照递增的次序排列
构造方法：我们可以用插入法，来获得。。不是很想打太多字了。方法叫做Stern-Brocot树。如果N无限大，那么这棵树就无限深。你可以用这个“二分”出一个无理数两端无限接近的分数
做题用处：不怎么知道

##同余的知识
这个烂大街了。。就是炒了一下冷饭
还有就是$ak\equiv bk(\mathrm{m}\mathrm{o}\mathrm{d}pk)$
可以得出$a\equiv b(\mathrm{m}\mathrm{o}\mathrm{d}p)$

##中国剩余定理与扩展中国剩余定理
用处：解同余方程
这个东西我以前没学过，今晚刚刚学的
放一下学习资料吧
中国剩余定理
扩展中国剩余定理
扩展中国剩余定理的板子：

#include<cstdio>
#include<cstring>
typedef long long LL;
LL exgcd (LL a,LL b,LL &x,LL &y)
{
	if (a==0)
	{
		x=0;y=1;
		return b;
	}
	LL tx,ty;
	LL d=exgcd(b%a,a,tx,ty);
	x=ty-(b/a)*tx;
	y=tx;
	return d;
}
int main()
{
	LL n;
	LL b1,m1;//第一个方程的余数和除数
	bool tf=true;
	scanf("%lld",&n);
	scanf("%lld%lld",&b1,&m1);
	for (LL u=2;u<=n;u++)
	{
		LL b2,m2;
		scanf("%lld%lld",&b2,&m2);
		LL A=m1,B=m2,C=b2-b1;
		LL X,Y;
		LL d=exgcd(A,B,X,Y);
		if (C%d!=0) {tf=false;break;}
		X=(X*(C/d)%(B/d)+(B/d))%(B/d);
		b1=m1*X+b1;
		m1=m1/d*m2;
	}
	if (!tf) printf("no solution!\n");
	else printf("%lld\n",b1);
	return 0;
}

#10.23晚
（今晚也没弄什么伟大的东西）
##一个不知道叫什么的定理
$0(modm),n(modm),2n(modm),3n(modm)......(m-1)n(modm)$,
设$d=gcd(n,m)$
这m个数将会按照某种次序恰好组成$m/d$个数的d个复制
我们可以得到
$jn\equiv kn(\mathrm{m}\mathrm{o}\mathrm{d}m)$
$j(n/d)\equiv k(n/d)(\mathrm{m}\mathrm{o}\mathrm{d}m/d)$
当$0\le k\le m/d$的时候，就会出现这d个复制
特别的，当d=1的时候，我们发现这些数刚好就是$0,1,2......m-1$
根据雀巢原理，当$n\perp m$的时候
$jn\equiv kn(\mathrm{m}\mathrm{o}\mathrm{d}m)$
$j\equiv k(\mathrm{m}\mathrm{o}\mathrm{d}m)$
由此可得，每隔m个数才会出现一组循环节

##费马小定理
性质$n^{p-1}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}m)$
p是质数且$n\perp p$

通过上面那个不知道什么东西可以知道：$n(modp),2n(modp)...(p-1)n(modp)$就是一个$1,2,3,4,5,6....p-1$的排列
所以$n\ast (2n)\ast .....\ast (p-1)n$在模p的意义下就是$(p-1)!$
所以$(p-1)!n^{p-1}\equiv (p-1)!(\mathrm{m}\mathrm{o}\mathrm{d}p)$

##费马大定理
对于任意一个n>2，对所有正整数a,b,c,n有
$a^n+b^n\ne c^n$
证明：没有

下面两个由于内容有点多，于是我想偷懒
#欧拉函数
欧拉定理：$n^{\varphi (m)}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d}m)$ 证明

其他的定理:${\sum }_{d|m}\varphi (d)=m$
这个的证明你可以吧m为分母所有的分数都列出来，然后化简分组
发现12的每一个因子都出现在分母上，一起出现的还有$\varphi (d)$个分子

#莫比乌斯函数
反演原理：略
递推式：略

#扩展欧拉定理

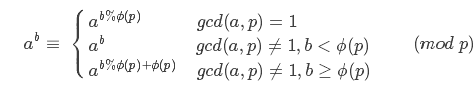
但其实我觉得第一种情况是可以并到第三种里面去的
因为当a,p互质的时候，根据费马小定理，你加上那个$\varphi (p)$是没有任何影响的
资料来源
我来说一下他里面的引理：

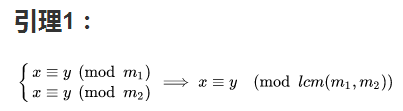
由第一个式子可得$(x-y)|m1$
由第二个式子可得$(x-y)|m2$
所以$(x-y)|lcm(m1,m2)$
知道了推论下面的就很简单了

这个的话，我的方法比较玄学
我们可以吧前面的函数值写出来，其实是$p^q-p^{q-1}$
化简可得$p^{q-1}\ast (p-1)$
由于p是大于1的正整数，p为素数，那么$p^{q-1}$最少就是2，后者的两倍也最少大2，显然比q要大

后面如果你可以牢记这两个推论，下面的路就好走了
盗图：

例题：相逢是问候

#10.24上午
做了很久的相逢是问候
然后求去学扩展Lucas了
感觉效率很低

##Lucas定理
当p是质数的时候，在模p的意义下
我不想写markdown了

C(n,m)=C(n%p,m%p)*C(n/p,m/p)

证明：没有
感觉这个还是蛮实用的

##扩展Lucas
这个的话，不需要p是质数，但是复杂度与p最大的质数的幂有关
学习资料
这里讲得特别好
例题
板子:

#include<cstdio>
#include<cstring>
typedef long long LL;
LL w[10];
LL n,m;
LL MOD;
LL need;//需要多少
LL pow (LL x,LL y,LL mod)
{
	if (y==0) return 1;
	if (y==1) return x;
	LL z=pow(x,y>>1,mod);
	z=z*z%mod;
	if (y&1) z=z*x%mod;
	return z;
}
LL mul (LL n,LL pi,LL pk)
{
	if (n==0) return 1;
	LL ans=1LL;
	for (int u=2;u<=pk;u++)
		if (u%pi!=0)
			ans=ans*u%pk;
	ans=pow(ans,n/pk,pk);
	for (int u=2;u<=n%pk;u++)
		if (u%pi!=0)
			ans=ans*u%pk;
	return ans*mul(n/pi,pi,pk)%pk;
}
void exgcd (LL a,LL b,LL &x,LL &y)
{
	if (a==0)
	{
		x=0;y=1;
		return ;
	}
	LL tx,ty;
	exgcd(b%a,a,tx,ty);
	x=ty-(b/a)*tx;
	y=tx;
	return ;
}
LL inv (LL A,LL mod)
{
	if (A==0) return 0;
	LL a=A,b=mod,x,y;
	exgcd(a,b,x,y);
	x=(x%b+b)%b;
	while (x<=0) x+=b;
	return x;
}
LL C (LL n,LL m,LL pi,LL pk)//从n个里面选m个   然后模数是pi的若干次幂，值为pk 
{
	if (m>n) return 0;
	LL a=mul(n,pi,pk),b=mul(m,pi,pk),c=mul(n-m,pi,pk);
	LL k=0,ans;
	for (int u=n;u>=1;u/=pi) k=k+u/pi;
	for (int u=m;u>=1;u/=pi) k=k-u/pi;
	for (int u=(n-m);u>=1;u/=pi) k=k-u/pi;
	ans=a*inv(b,pk)%pk*inv(c,pk)%pk*pow(pi,k,pk)%pk;	
	return ans*(MOD/pk)%MOD*inv(MOD/pk,pk)%MOD;
}
int main()
{
	scanf("%lld",&MOD);
	scanf("%lld%lld",&n,&m);
	for (LL u=1;u<=m;u++) 
	{
		scanf("%lld",&w[u]);
		need+=w[u];
	}
	if (need>n)
	{
		printf("Impossible\n");
		return 0;
	}
	LL shen=1;
	for (int i=1;i<=m;i++)
	{
		LL P=MOD;
		LL now=0;
		for (LL u=2;u*u<=P;u++)
			if (P%u==0)
			{
				LL pk=1LL;
				while (P%u==0)	pk*=u,P/=u;
				now=(now+C(n,w[i],u,pk))%MOD;
			}
		if (P>1) now=(now+C(n,w[i],P,P))%MOD; 
		shen=shen*now;
		n-=w[i];
	}
	printf("%lld\n",shen%MOD);
	return 0;
}

#高次同余方程
BSGS：师姐的博客
感觉这个方法还是有点暴力，居然是根号的。。
由于有点事，具体的东西就不写了，以后再填吧
板子：

LL bsgs (LL a,LL b,LL p)//a^x%p=b
{
	map<LL,LL> mp;
	mp.clear();
	a%=p;b%=p;
	if (a==0&&b==0) return 1;
	if (a==0) return -1;
	LL m=ceil(sqrt(p));
	LL lalal=1%p;
	for (LL u=0;u<m;u++)
	{
		if (mp.count(lalal)==0)
			mp[lalal]=u;
		lalal=lalal*a%p;
	}
	lalal=inv(lalal,p);
	for (LL u=0;u<m;u++)
	{
		if (mp.count(b))
			return u*m+mp[b];
		b=b*lalal%p;
	}
	return -1;
}

#11.19 下午
在NOIP爆炸之后，沉迷了文化课后，我决定又开坑了。。
反正NOIP爆炸都准备退役了是吧，哪不如学点数学到时候没准可以装逼

##线性求逆元
如果你需要求1~n里面所有数关于p的逆元
如果你一个一个求的话，是$O(nlogn)$的
但是这个很显然会有$O(n)$的方法
我们不妨设$k\ast i+b=p$
把他放进$modp$的意义下
就是$k\ast i+b\equiv 0(\mathrm{m}\mathrm{o}\mathrm{d}p)$
如果我们把两边都乘上$i^{-1}$,$b^{-1}$
你就会得到式子
$k\ast b^{-1}+i^{-1}=0$
$i^{-1}=-k\ast b^{-1}$
于是你就可以线性求逆元了
k是什么大家应该都知道吧。。

A[i] = -(p / i) * A[p % i];

##线性求阶乘的逆元
这个也十分简单了啊

inv[i]=inv[i+1]*(i+1)

这个应该很好理解吧。。
这样的话你先预处理出阶乘
然后求出最后一个的逆元
就可以推回去了

##鸽巢原理
也叫抽屉原理。这个大家都会把，我就不写了。。
##扩展鸽巢原理
如果$q_1,q_2,q_3.....q_n$是正整数，如果将$q_1+q_2+q_3+q_4+....q_n-n+1$个物体放进n个格子里
那么或者第一个格子有至少$q_1$个物体，那么或者第二个格子有至少$q_2$个物体,那么或者第三个格子有至少$q_3$个物体
证明：显然，不写了
##一个由扩展鸽巢原理推出来的结论
你现在有$n^2+1$个正整数组成的一个序列，那么一定存在有一个长度为n+1的递增子序列或者递减子序列
如果我们可以证明出如果没有长度为$n+1$的递增子序列，那么肯定存在有长度为$n+1$的递减子序列，那么结论就成立了
证明：
如果不存在一个n+1的递增子序列
我们设以i开头的递增子序列最长长度为$m_i$
那么$m$的取值范围就是$1到n$
于是可以得到，有$n+1$个$m$是一样的
稍微想一下就知道，这$n+1$个肯定是递减的
然后就没有了

##一些小定义吧
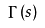=(n-1)!
证明（我也没看）
上升阶乘幂$x^n$(n的上面有一条横线）=(x+n-1)!/(x-1)!
下降阶乘幂$x^n$(n的下面有一条横线）=x!/(x-n)!

#11.20~?
##关于二项式系数的研究
###定义
符号$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$就是二项式系数，其实这个东西就和排列组合差不多，其实我感觉基本上就是一样的。但是似乎这个东西，对于n和k取任意实数都是由意义的。。（虽然我不知道意义是什么）
意义就是从n个东西里面选出k个有多少种方案
###基本恒等式
1.
$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\left(\genfrac{}{}{0ex}{}{n}{n-k}\right)$

$\left(\genfrac{}{}{0ex}{}{r}{k}\right)=\frac{r}{k}\left(\genfrac{}{}{0ex}{}{r-1}{k-1}\right)$
这个的话你大概推一下式子就出来了

$k\left(\genfrac{}{}{0ex}{}{r}{k}\right)=r\left(\genfrac{}{}{0ex}{}{r-1}{k-1}\right)$
这个就是上一个东西的变形而已

$(r-k)\left(\genfrac{}{}{0ex}{}{r}{k}\right)=r\left(\genfrac{}{}{0ex}{}{r-1}{k}\right)$
证明：$(r-k)\left(\genfrac{}{}{0ex}{}{r}{k}\right)=(r-k)\left(\genfrac{}{}{0ex}{}{r}{r-k}\right)=r\left(\genfrac{}{}{0ex}{}{r-1}{r-k-1}\right)=r\left(\genfrac{}{}{0ex}{}{r-1}{k}\right)$

$\left(\genfrac{}{}{0ex}{}{r-1}{k}\right)=\left(\genfrac{}{}{0ex}{}{r-1}{k}\right)+\left(\genfrac{}{}{0ex}{}{r-1}{k-1}\right)$
这个大家用的应该很多了吧，就是排列组合线性的递推式啊
证明有很多，感性地证明，推导式子的证明都可以。我这里写一个通过上面式子推导的证明：
$(r-k)\left(\genfrac{}{}{0ex}{}{r}{k}\right)+k\left(\genfrac{}{}{0ex}{}{r}{k}\right)=r\left(\genfrac{}{}{0ex}{}{r-1}{k}\right)+r\left(\genfrac{}{}{0ex}{}{r-1}{k-1}\right)$
左边的很明显等于$r\left(\genfrac{}{}{0ex}{}{r}{k}\right)$,然后两边同除$r$就可以了

6.如果你对上面这个递推式大力展开，我们还可以得到另外两个有用的东西
${\sum }_{k=0}^n\left(\genfrac{}{}{0ex}{}{r+k}{k}\right)=\left(\genfrac{}{}{0ex}{}{r}{0}\right)+\left(\genfrac{}{}{0ex}{}{r+1}{1}\right)+...+\left(\genfrac{}{}{0ex}{}{r+n}{n}\right)=\left(\genfrac{}{}{0ex}{}{r+n+1}{n}\right)$
${\sum }_{k=0}^n\left(\genfrac{}{}{0ex}{}{k}{m}\right)=\left(\genfrac{}{}{0ex}{}{0}{m}\right)+\left(\genfrac{}{}{0ex}{}{1}{m}\right)+...+\left(\genfrac{}{}{0ex}{}{n}{m}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{m+1}\right)$

7.$\left(\genfrac{}{}{0ex}{}{r}{m}\right)\left(\genfrac{}{}{0ex}{}{m}{k}\right)=\left(\genfrac{}{}{0ex}{}{r}{k}\right)\left(\genfrac{}{}{0ex}{}{r-k}{m-k}\right)$
这个的话，你可以把他化成阶乘相除的形式，然后分子分母同乘$(r-k)!$
如果你知道了这个，$2$就是他$k=1$的一个特殊情况了

然后我自己YY了一道题，大概是这样的

已知r和k
求${\sum }_{m=k}^r\left(\genfrac{}{}{0ex}{}{r}{m}\right)\left(\genfrac{}{}{0ex}{}{m}{k}\right)$
做法也十分简单，你就用第7个恒等式，然后就可以将$\left(\genfrac{}{}{0ex}{}{r}{k}\right)$这个常数项提出来，剩下的就是一个二项式定理了。具体正确性我还没验证，但应该是对的

#快速傅里叶变化
我也不知道这个算不算数学知识，应该，我感觉，算吧。。
具体看黑书——算导，我就不说了其实是我也不是特别懂原根
先贴一个板子(FFT):
题目就是uoj的多项式乘法了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#include<complex>
using namespace std;
const double pi=M_PI;
const int N=1000005;
int n,m;
complex<double> a[N],b[N];
void fft (complex<double> *a,int n,int o)
{
	if (n==1) return ;
	int k=(n>>1);
	complex<double> w=1,wn(cos(2*pi/n),o*sin(2*pi/n)),a0[k],a1[k];
	for (int u=0;u<k;u++)
	{
		int i=u*2;
		a0[u]=a[i];
		a1[u]=a[i+1];
	}
	fft(a0,k,o);fft(a1,k,o);
	for (int u=0;u<k;u++)
	{
		a[u]=a0[u]+w*a1[u];
		a[u+k]=a0[u]-w*a1[u];
		w=w*wn;
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int u=0;u<=n;u++) scanf("%lf",&a[u]);
	for (int u=0;u<=m;u++) scanf("%lf",&b[u]);
	m=m+n;n=1;while (n<=m) n<<=1;
	fft(a,n,1);fft(b,n,1);
	for (int u=0;u<=n;u++) a[u]*=b[u];
	fft(a,n,-1);
	for (int u=0;u<=m;u++)
		printf("%d ",(int)(a[u].real()/n+0.5));
	return 0;
}