斐波那契相关

最新推荐文章于 2023-10-26 10:55:26 发布
最新推荐文章于 2023-10-26 10:55:26 发布
阅读量313 收藏
点赞数
分类专栏： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_37050329/article/details/89174838
版权

 

一、引入

有趣问题：

1，有一段楼梯有10级台阶,规定每一步只能跨一级或两级,要登上第10级台阶有几种不同的走法?

答：这就是一个斐波那契数列：登上第一级台阶有一种登法；登上两级台阶，有两种登法；登上三级台阶，有三种登法；登上四级台阶，有五种方法……所以，1，2，3，5，8，13……登上十级，有89种。

2，数列中相邻两项的前项比后项的极限是多少，就是问，当n趋于无穷大时，F(n)/F(n+1)的极限是多少？

答：这个可由它的通项公式直接得到，极限是(-1+√5)/2，这个就是所谓的黄金分割点，也是代表大自然的和谐的一个数字。

 数学表示：

Fibonacci数列的数学表达式就是：

F(n) = F(n-1) + F(n-2)

F(1) = 1

F(2) = 1

二、解法

1、递归

递归解法（效率非常低）
long long Fibonacci_Solution1(unsigned int n)
{
  if(n <= 0)
     return 0;

  if(n == 1)
     return 1;

  return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);
}

2、非递归

自下而上计算，首先根据f(0) 和f(1)算出f(2)，再根据f(1)和f(2)算出f(3)……依此类推，可以算出第n项

long long Fibonacci(unsigned n)
{
    int result[2] = {0 , 1};
    if(n < 2)
        return result[n];

    long long fibMinusOne = 1;
    long long fibMinusTwo = 0;
    for(unsigned int i = 2 ; i <= n ; ++i)
    {
        fibN = fibMinusOne + fibMinusTwo;

        fibMinusTwo = fibMinusOne;
        fibMinusOne = fibN;
    }

    return fibN;
}

三、例题

1、假如有一只青蛙，一次可以跳上 1 级台阶，也可以跳 2 级台阶，请问青蛙上一个 n 级台阶一共有多少种跳法？

  1. 假如现在台阶只有 1 级，n = 1，那么这只青蛙就在只有 1 种跳法：1（1 代表一次跳 1 级台阶）也就是 f(1) = 1 种跳法
  2. 假如现在台阶只有 2 级，n = 2，那么这只青蛙可以有 2 种跳法：1 1、2（1 代表一次跳 1 级台阶，2 代表一次跳 2 级台阶），也就是 f(2) = 2 种跳法
  3. 假如现在台阶有 3 级，n = 3，青蛙可以有几种跳法呢？
    假如青蛙先跳了 1 级台阶，还剩下 2 级台阶，那它还有几种跳法呢？通过第 2 个情况分析知道有 2 种跳法；假如青蛙先跳了 2 级台阶，根据第 1 个情况分析知道有 1 种跳法，所以这时候得出 f(3) = 2 + 1 种方法
  4. 假如现在台阶有 4 级，n = 4，我们利用上面的规律继续分析可得：f(4) = 3 + 2

综上所述，我们得出其实这个算法就是一个（变形）斐波那契数列问题，公式如下：

  • n = 1, f(1) = 1
  • n = 2, f(2) = 2
  • n > 2, f(n) = f(n -1) + f(n -2)
#include <stdio.h>
/* 优化后的方法 */
long long Fibonacci(unsigned n)
{
    int result[2] = {0, 1, 2};
    if(n <= 2)
        return result[n];
    
    long long  fibNMinusOne = 2;
    long long  fibNMinusTwo = 1;
    long long  fibN = 0;
    for(unsigned int i = 3; i <= n; ++ i)
    {
        fibN = fibNMinusOne + fibNMinusTwo;
        
        fibNMinusTwo = fibNMinusOne;
        fibNMinusOne = fibN;
    }
    
    return fibN;
}

int main(int argc, const char * argv[]) {
    clock_t start, finish;
    double  duration;
    /* 测量一个事件持续的时间*/
    /* 起始 */
    start = clock();
    /* 要执行的代码，放在此处（两个clock方法的调用中间），方便测试出要执行的代码的执行时间 */
    printf("%lld\n", Fibonacci(11));
    /* 结束 */
    finish = clock();
    /* 时间 */
    duration = (double)(finish - start) / CLOCKS_PER_SEC;
    printf( "Use time is %f seconds.\n", duration );
    return 0;
}

2、一仅仅青蛙一次能够跳上1级台阶，也能够跳上2级，也能跳上n级，求其有多少种解法。

用数学归纳法能够证明：f(n)=2^(n-1)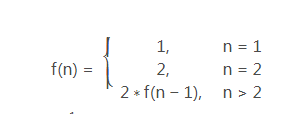

long long FrogJump12nStep(int n)
{
    if (n <= 0)
    {
        std::cerr << "param error" << std::endl;
        return -1;
    }
    else if (n == 1)
        return 1;
    else
    {
        long long  fn1 = 1;
        long long fn = 0;
        for (int i = 2; i <= n;++i)
        {
            fn = 2 * fn1;
            fn1 = fn;
        }
        return fn;
    }
}

3、小矩形覆盖大矩形，用2*1的小矩形横着或竖着去覆盖各大矩形。

思路：设题解为f(n),

第一步：若第一块矩形竖着放，后边还有n-1个2*1矩形，即此种情况下，有f(n-1)种覆盖方法。
第二部：若第一块横着放。后边还有n-2个2*1矩形，此种情况下，有f(n-2)种覆盖方法。

可得 f(n)=f(n-1)+f(n-2)

四、优化

1、矩阵算法求解

uint64_t fibonacci(unsigned int n) {
    uint64_t m[2][2] = { 1,1,1,0 }; // 1次矩阵
    uint64_t result[][2] = { 1,0,0,1 }; // 单位矩阵
    uint64_t temp[2][2];
    // 计算n次矩阵
    for (unsigned int i = 1; i <= n; i++) {
        temp[0][0] = result[0][0] * m[0][0] + result[0][1] * m[1][0];
        temp[0][1] = result[0][0] * m[0][1] + result[0][1] * m[1][1];
        temp[1][0] = result[1][0] * m[0][0] + result[1][1] * m[1][0];
        temp[1][1] = result[1][0] * m[0][1] + result[1][1] * m[1][1];
        memcpy(result, temp, sizeof(uint64_t) * 4);
    }
    // result[1][0] * 1 + result[1][1] * 0;
    return result[1][0] * 1;
}

该算法在时间上也是按线性增长的：O(N)，由于for循环内指令较多，所以可能会比循环迭代算法更耗时。但是该算法有很多可优化的地方。

2、矩阵快速幂优化矩阵算法

在计算整数的乘法时，计算机底层是通过加法和移位运算实现的，举个例子：

十进制：4*13 => 二进制：100b*1101b = 100b*(1000b+100b+00b+1b) = (100b<<3)+(100b<<2)+0+(100b<<1)
快速幂：对于幂运算，我们也可以用类似的方式进行优化。

通常我们进行幂运算会直接循环累积，比如：4^13，会循环13次。

但是如果我们使用乘法的结合律就可以将时间复杂度降到O(log(N))：

4^13 = (4^8) + (4^4) + (4^1) ;
4^8 = 4^4 * 4^4;
4^4 = 4^2 * 4^2;
4^2 = 4*4;

int quick_pow(int base, int exp) {
    int result = 1;
    while (exp) {
        if (exp & 1)
            result *= base;
        exp >>= 1;
        base *= base; // 2,4,8...次幂
    }
    return result;
}

我们可以把快速幂的思想应用到矩阵运算上，从而对上面的矩阵算法进行优化：

uint64_t fibonacci(unsigned int n) {
    uint64_t m[2][2] = { 1,1,1,0 }; // 1次矩阵
    uint64_t result[][2] = { 1,0,0,1 }; // 单位矩阵
    uint64_t temp[2][2];
    while (n) {
        if (n & 1) {
            temp[0][0] = result[0][0] * m[0][0] + result[0][1] * m[1][0];
            temp[0][1] = result[0][0] * m[0][1] + result[0][1] * m[1][1];
            temp[1][0] = result[1][0] * m[0][0] + result[1][1] * m[1][0];
            temp[1][1] = result[1][0] * m[0][1] + result[1][1] * m[1][1];
            memcpy(result, temp, sizeof(uint64_t) * 4);
        }
        // 2、4、8...次幂矩阵
        temp[0][0] = m[0][0] * m[0][0] + m[0][1] * m[1][0];
        temp[0][1] = m[0][0] * m[0][1] + m[0][1] * m[1][1];
        temp[1][0] = m[1][0] * m[0][0] + m[1][1] * m[1][0];
        temp[1][1] = m[1][0] * m[0][1] + m[1][1] * m[1][1];
        memcpy(m, temp, sizeof(uint64_t) * 4);
        n >>= 1;
    }
    // result[1][0] * 1 + result[1][1] * 0;
    return result[1][0] * 1;
}

3、使用常量优化

为了减少计算2、4、8…次幂矩阵所消耗的时间，我们可以提前把这些矩阵幂求出来并存在常量表中，这样可以减少乘法运算的次数。

先写个程序自动生成常量表

void power_matrix(uint64_t m[][2], unsigned int exp) {
    uint64_t result[][2] = { 1,0,0,1 }; // 单位矩阵
    uint64_t temp[2][2];
    // 计算n次矩阵
    for (unsigned int i = 1; i <= exp; i++) {
        temp[0][0] = result[0][0] * m[0][0] + result[0][1] * m[1][0];
        temp[0][1] = result[0][0] * m[0][1] + result[0][1] * m[1][1];
        temp[1][0] = result[1][0] * m[0][0] + result[1][1] * m[1][0];
        temp[1][1] = result[1][0] * m[0][1] + result[1][1] * m[1][1];
        memcpy(result, temp, sizeof(uint64_t) * 4);
    }
    memcpy(m, result, sizeof(uint64_t) * 4);
}
void generate_matrix() {
    uint64_t m[2][2] = { 1,1,1,0 }; // 1次矩阵
    uint64_t temp[2][2];
    for (int i = 0; i < 8; i++) {
        memcpy(temp, m, 4 * sizeof(uint64_t));
        printf("{");
        power_matrix(temp, 1 << i);
        for (int j = 0; j < 2; j++) {
            for (int k = 0; k < 2; k++) {
                printf("%llu, ", temp[j][k]);
            }
        }
        printf("},\n");
    }
}

调用generate_matrix函数生成0~7次矩阵。

把生成的常量表复制粘贴到代码中：

uint64_t fibonacci6(unsigned int n) {
    const static uint64_t cache[][2][2] = {
        { 1, 0, 0, 1 },// 0次幂(无用)
        { 1, 1, 1, 0 },// 1次幂(2^0,1)
        { 2, 1, 1, 1 },// 2次幂(2^1,2)
        { 5, 3, 3, 2 },// 4次幂(2^2,3)
        { 34, 21 ,21, 13 },// 8次幂(2^3,4)
        { 1597, 987, 987 ,610 },// 16次幂(2^4,5)
        { 3524578, 2178309, 2178309, 1346269 },// 32次幂(2^5,4)
        { 17167680177565, 10610209857723, 10610209857723, 6557470319842},//64次幂(2^6,5)
        { 8102862946581596898, 18154666814248790725, 18154666814248790725, 8394940206042357789}//128次幂(2^7,6)
    };
    uint64_t result[][2] = { 1,0,0,1 }; // 单位矩阵
    uint64_t temp[2][2];
    int bit_pos = 1;
    while (n) {
        if (n & 1) {
            temp[0][0] = result[0][0] * cache[bit_pos][0][0] + result[0][1] * cache[bit_pos][1][0];
            temp[0][1] = result[0][0] * cache[bit_pos][0][1] + result[0][1] * cache[bit_pos][1][1];
            temp[1][0] = result[1][0] * cache[bit_pos][0][0] + result[1][1] * cache[bit_pos][1][0];
            temp[1][1] = result[1][0] * cache[bit_pos][0][1] + result[1][1] * cache[bit_pos][1][1];
            memcpy(result, temp, sizeof(uint64_t) * 4);
        }
        n >>= 1;
        bit_pos++;
    }
    // result[1][0] * 1 + result[1][1] * 0;
    return result[1][0] * 1;
}

这种方法的缺点是所能求的斐波那契最大项决定于表的大小，上面代码实现中所能求的最大项是255(八位全1的情况)，不过斐波那契数列的第94项就已经超过64位无符号整形了。

(第93项斐波那契数为1220 0160 4151 2187 6738，而64位无符号整形最大值为2^64-1=1844 6744 0737 0955 1615，第94项为1974 0274 2198 6822 3167溢出就成了129 3530 1461 5867 1551)

如果想要求更大的斐波那契数，则需要自己实现一个类似于Java中的BigInteger类(C++应该会有很多类似的开源库)
4、通向式优化

求斐波那契数列通项有很多种方法，这里用最容易理解的方法进行求解：初等代数进行数列代换。

这种方法只要有高中数学水平就可以解出来(当时高中解出来的时候，还以为是什么天大的发现^_^)。

/* 通项公式直接求解 */
uint64_t fibonacci6(unsigned int n) {
    const double sqrt5 = 2.2360679774997896964091736687313;
    const double a = (sqrt5 + 1) / 2;
    const double b = (1 - sqrt5) / 2;
    const double sqrt1_5 = 1 / sqrt5;

    return (uint64_t)((pow(a, n) - pow(b, n))*sqrt1_5);
}

5、测试

/* 计算时间间隔 */
double duration(struct timespec *end, struct timespec *start) {
    double d_sec = difftime(end->tv_sec, start->tv_sec);
    long d_nsec = end->tv_nsec - start->tv_nsec;
    return (d_sec*10e9 + d_nsec);
}

/* 算法测试 */
void compare_and_test() {
    typedef uint64_t(*PFUNC)(unsigned int n);
    PFUNC pFuncs[] = { fibonacci2 ,fibonacci3, fibonacci4, fibonacci5, fibonacci6 };
    struct timespec start, end;
    for (int j = 0; j < sizeof(pFuncs) / sizeof(PFUNC); j++) {
        timespec_get(&start, TIME_UTC);
        // 93项后会发生溢出，这里测试计算时间，不关心溢出问题
        for (int i = 0; i < 95; i++) {
#           ifdef NDEBUG
            (*pFuncs[j])(i);
#           else
            printf("%llu ", (*pFuncs[j])(i));
#           endif
        }
        timespec_get(&end, TIME_UTC);
        printf("\t duration: %lf nanosecond\n", duration(&end, &start));
    }
}

结论：项数越大，快速幂的效果越明显

兰亭落雪
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
bitset_ex高级版，支持operator[]取值和赋值
拔剑—浆糊的传说
12-29 115
// Example program #include < iostream > #include < string > #include < cstring > #include < cassert > using namespace std; class bitset_ex { public: bitset_ex(const ...
斐波那契数列
weixin_43659449的博客
07-05 321
题目： 写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下： F(0) = 0, F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。 答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。 示例 1： 输入：n = 2 输出：1 示例 2： 输入：n = 5 输出：5 来源：力扣（Le
聊聊Doris向量化执行引擎-过滤操作
帅的数说
05-07 393
聊聊Doris向量化执行引擎-过滤操作Doris是开源的新一代极速MPP数据库，和StarRocks同源，采用全面向量化技术，充分利用CPU单核资源，将单核执行性能做到极致。本文，我们聊聊过滤操作是如何利用SIMD指令进行向量化操作。过滤操作的SIMD向量化函数是_evaluate_vectorization_predicate：和StarRocks实现大致类似，但稍有不同： SegmentIt...
斐波那契数列（C/C++）
热门推荐
m0_71934846的博客
03-20 1万+
斐波那契数列（C/C++）
C语言求Fibonacci斐波那契数列通项问题的解法总结
09-02
斐波那契数列相关问题是考研和ACM中常见的算法题目,这里特地为大家整理了C语言求Fibonacci斐波那契数列通项问题的解法总结,需要的朋友可以参考下
用Python实现斐波那契（Fibonacci）函数
09-21
主要介绍了用Python实现斐波那契（Fibonacci）函数的相关资料,需要的朋友可以参考下
毕业设计有关斐波那契分形曲线的相关分析MATLAB.zip
08-30
毕业设计有关斐波那契分形曲线的相关分析MATLAB.zip毕业设计有关斐波那契分形曲线的相关分析MATLAB.zip毕业设计有关斐波那契分形曲线的相关分析MATLAB.zip毕业设计有关斐波那契分形曲线的相关分析MATLAB.zip毕业设计...
java实现Fibonacci算法实例
09-03
主要介绍了java实现Fibonacci算法的方法,以实例形式较为详细的分析了java实现Fibonacci算法的原理与相关技巧,具有一定参考借鉴价值,需要的朋友可以参考下
毕业设计-基于MATLAB+有关斐波那契分形曲线的相关分析
06-09
毕业设计有关斐波那契分形曲线的相关分析MATLAB 1.阅读参考文献，掌握Fibonacci序列的定义，了解其性质。 2.学习如何利用L系统从序列出发构造分形曲线，并学习利用Matlab、Maple等作图的方法。 3.学习盒维数的定义和...
输出斐波那契数列直到溢出
05-06
write a program tg\ fd
斐波那契
03-09
long fib4 (int n) { Matrix matrix0(1, 1, 1, 0); matrix0 = power(matrix0, n-1); return matrix0.matr[0][0]; }
最优化-斐波那契数列（fibonacci）优化方法 算法原理及代码实现
最新发布
weixin_46668520的博客
10-26 1970
本文介绍了Fibonacci数列优化的原理，并详细的用pytho实现其算法。
【C/C++】斐波那契数列数列系列问题详解
qq_62662919的博客
12-11 1万+
🍉、什么是斐波那契数列？斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N🍉、怎么定义斐波那契数列。
【坚持每日一题9.4】斐波那契数列
kangbin825的专栏
09-04 130
写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下： F(0) = 0,   F(1) = 1 F(N) = F(N - 1) + F(N - 2), 其中 N > 1. 斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。 答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。 示例 1： 输入：n = 2 输出：1 示例 2： 输入
洛谷 P1255 数楼梯(斐波那契数列+高精度加法)
Thy__father的博客
05-28 609
菜鸟生成记(69) P1255 数楼梯 由题意得:求斐波那契数列第n项; 0<=n<=5000;数列的第94项左右就已经超出long long 的数据范围了,所以只能用高精度加法 #include<iostream> #include<cstring> using namespace std; const int N=5e3+100; const int M=1e3+100; struct st{ int a[M];//储存大数(超出long long) int l
Fibonacci python
09-14
在中，我们可以使用SymPy库提供的Fibonacci类来计算斐波那契数列。下面是一个示例代码： ```python from sympy import fibonacci prev10 = [fibonacci(n) for n in range(10)] print(prev10) ``` 运行这段代码将输出前10个斐波那契数列的值：[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]。这段代码使用了SymPy库中的fibonacci函数，通过列表推导式生成了前10个斐波那契数列的值。 斐波那契数列是一种特殊的数列，它的定义是F(1)=1，F(2)=1，而对于n大于等于3的情况，斐波那契数列的第n项等于前两项之和，即F(n)=F(n-1)+F(n-2)。这个数列以兔子繁殖为例子而引入，因此也被称为兔子数列。 如果你对斐波那契数列和相关性质更感兴趣，你可以参考一些关于斐波那契数列的书籍，比如"The Best Books about Fibonacci and the Fibonacci Sequence"。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值