sklearn-1.1.15.鲁棒性回归：异常值模型错误

1.1.15.鲁棒性回归：异常值和模型错误

鲁棒回归适用于数据异常的回归模型：异常值或出现模型错误。

1.1.15.1.不同的场景和有用的概念

x异常还是y异常？

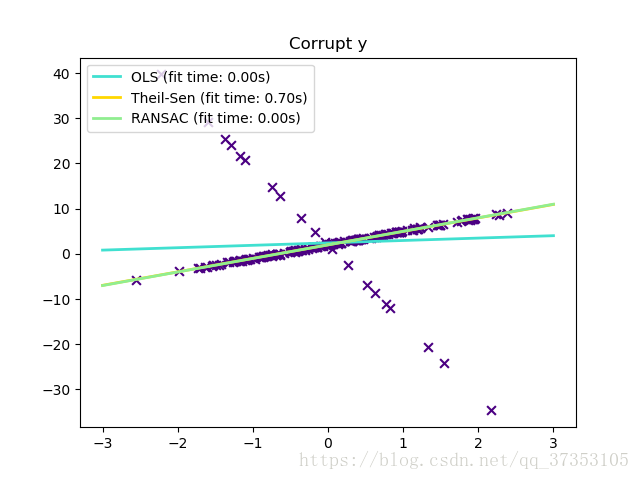
当y是异常值时

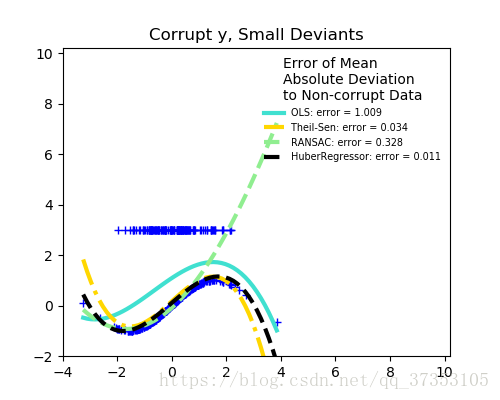
当x异常时

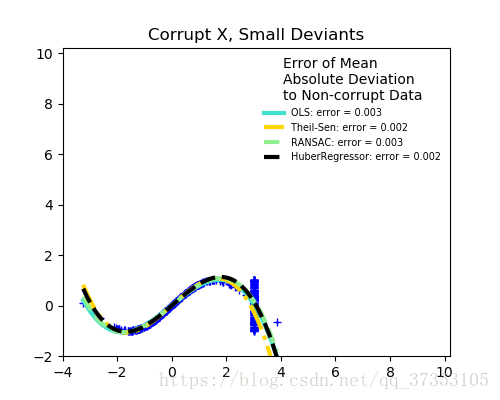
异常值的分数与误差幅度的关系

离群点的数量很重要，但是有多少是离群点。

离群点较少的时候

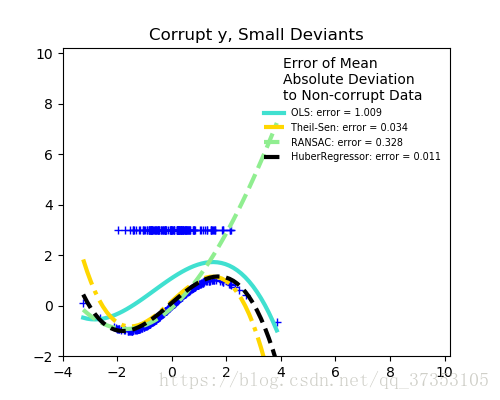
离群点较多的时候

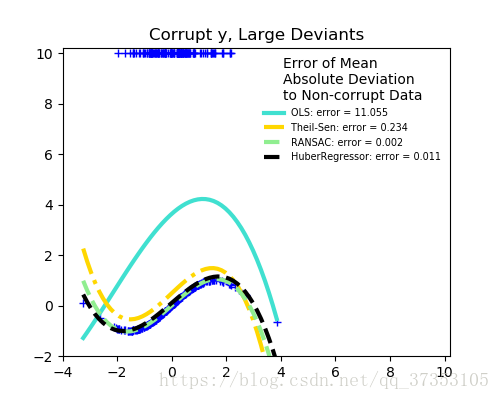
稳健拟合的一个重要的概念就是分解点：可能一小部分的偏离合适的数据，失去依附数据。

注意，一般来说，高维设置的鲁棒性拟合很困难。这里的健壮模型可能不适合这些设置。

权衡：使用什么估计？

        scikit-learn提供了三个强大的回归估计：RANSAC、TheilSen以及HuberRegressor。

            RANSAC比RANSAC和TheilSEN要快当数据集很大的时候，例如样本远大于特征值。这时因为RANSAC和THeilSen适合小的数据集。然而，TheilSen和RanSAC都不像HuberRegressor那样默认提供强大的参数。

            RANSAC比TheilSen快，并且随着样本的增加而增加。

            RANSAC在处理大量的x和y异常表现得更好。

            TheilSen处理中等大小的x异常，但是这种属性会因为特征值的增加而消失。

如果有疑问，请看下面的RANSAC。

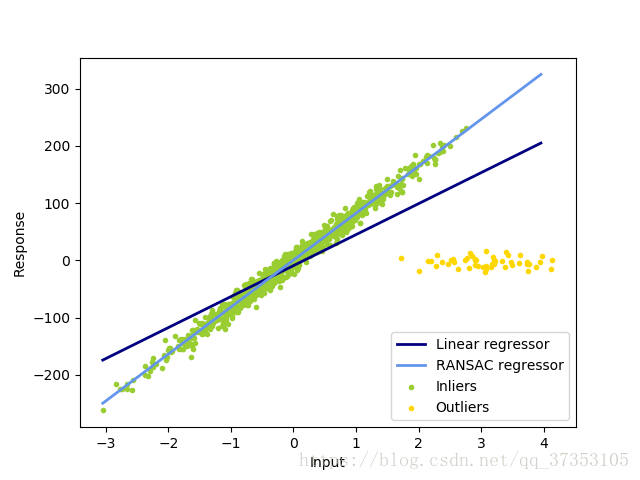
1.1.15.2RANSAC 随机样本共识

RANSAC适用于整个数据集中的子集模型。

RANSAC是一种非确定性算法，只能确定一定的概率下合理的结果，这取决于迭代的次数（阅读max_trials参数）。

它通常被用于线性和非线性回归问题，在摄影测量计算机视觉领域特别受欢迎。

这个算放将整个输入的数据分割为一组内点，可能会收到噪音和异常值的影响，例如错误的估量结果或者对数据的无效假设。只从确定的内部估计中得到模型。

1.1.15.2.1算法的细节

每次迭代都会执行下面5步：

1、选择min_samples随机的最小值并确定是否有效is_data_vaild

2、将模型拟合到随机子集（base_estimator.fit）检查估计模型是否有效is_data_vaild

3、通过计算估计模型的残差（base_estimator.predict（X） - y）将所有数据分类为内点或外点。 - 绝对残差小于residual_threshold的所有数据样本均视为内点。

4、如果内部样本数量最大，则将拟合模型保存为最佳模型。 如果当前估计的模型具有相同数量的内点，则只有它具有较好的分数才被认为是最好的模型。

这些步骤可以执行的最大次数（max_trials）直到满足停止条件（参考stop_N_inliners和stop_score）。使用先前确定的最佳模型的所有的inlner样本来估计最后的最终模型。

is_data_valid和is_model_valid函数允许识别和拒绝随机子样本的退化组合。如果不需要估计模型来识别退化情况，则应该使用is_data_valid，因为它在拟合模型之前被调用，从而能够有更好的计算性能。

例子

RANSAC的鲁棒性模型估计

参考

• https://en.wikipedia.org/wiki/RANSAC
• “Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography” Martin A. Fischler and Robert C. Bolles - SRI International (1981)

• “Performance Evaluation of RANSAC Family” Sunglok Choi, Taemin Kim and Wonpil Yu - BMVC (2009)

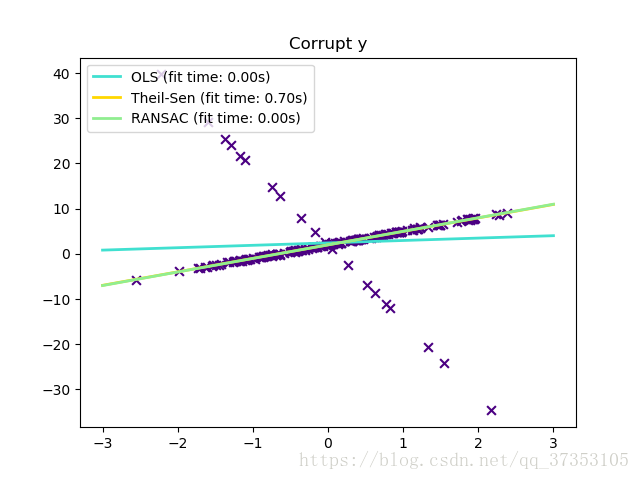
1.1.15.3.Theil-Sen估计：基于广义值的估计量

TheilSenRegressor估计使用多维中值的泛化。因此对于多变量异常值效果很好。注意，估计的鲁棒性随着问题的维数快速下降。它失去了它的鲁棒性，并不会比一个最小二乘的高维效果好。

例子

Theil-Sen回归

鲁棒性估计拟合

参考

• https://en.wikipedia.org/wiki/Theil%E2%80%93Sen_estimator

1.1.15.3.1.理论考虑

TheilSenRegressor在渐进的效率上和无偏估计方面与普通最小二乘法相当。与OLS想法，Theil-Sen是一种非参数方法，这个意味着它不会假设数据的分布。由于Theil-Sen是一个基于中值估计的，它对与破坏性的数据更加的稳健。在单变量设置中，Theil-Sen在简单线性回归分解点约29.3%，这意味着它最高容忍29.3%的容易破坏数据。

在scikit-learn中的TheilSenRegressor中遵循多元线性回归的推广，使用中位数是一个中值到多维的泛化。

在时间和空间的复杂性方面，Theil-Sen按照

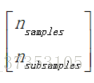
这使得无法应对大量样本的特征问题是不可行的。因此，通过考虑所有组合的随机子集，可以选择子群的大小来限制时间和空间复杂度。

例子

Theil-Sen回归

参考

References:

[8]	Xin Dang, Hanxiang Peng, Xueqin Wang and Heping Zhang: Theil-Sen Estimators in a Multiple Linear Regression Model.

[9]	Kärkkäinen and S. Äyrämö: On Computation of Spatial Median for Robust Data Mining.

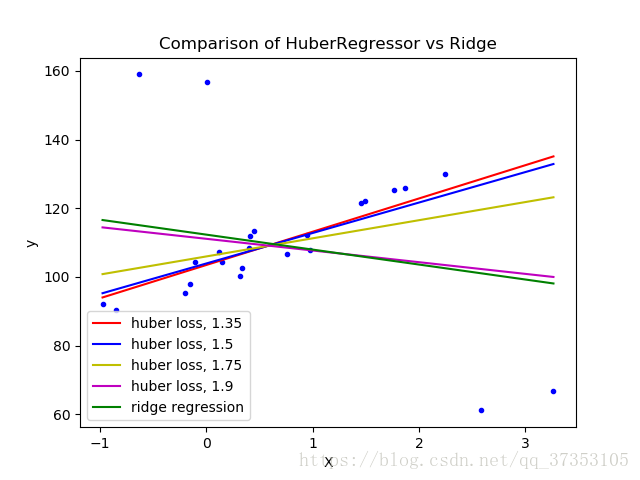
1.1.15.4.Huber回归

HuberRegressor与Ridge不同，因为它将线性损失应用于归类为异常样本。如果样本的绝对误差小于某一个阈值，则样本将会归类为内部样本。它与TheilSenRegressor和RANSACRegressor不同，因为它不会忽略异常值的影响，但对它们的权重较小。

HuberRegressor的损失函数的最小给出为：

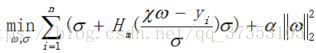
以及

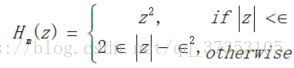
建议将参数epsilon设置为1.35以达到95%的统计效率

1.1.15.5注意

HuberRegressor与使用的SGDRegressor不同之处在于以下损失的设置。

    HuberRegressor的缩放不变，一旦决定了epsilon，将x和y向上或向下缩放不同的值将产生与之前相同的鲁棒性。与SGDREgressor相比，当x和y缩放时，必须再次设置epsilon。

       HuberRegressor应该更有效的用于少量的样本，而SGDRegressor需要多次训练数据传递以产生相同的鲁棒性。

例子

Huber回归vs岭回归在数据集上具有强的差异性

参考

• Peter J. Huber, Elvezio M. Ronchetti: Robust Statistics, Concomitant scale estimates, pg 172

此外，这类估计与Robust回归的R实现不同(http://www.ats.ucla.edu/stat/r/dae/rreg.htm)因为R的实现是基于残差大于特定阈值的多少来给每个样本赋予权重的加权最小二乘实现。