文章目录
专栏博客链接
查阅相关链接
前引
还有两篇就要写完了 这五六篇就在今晚把他全部写出来发了 因为待会回寝室自己还得抄大物实验 大物实验老师坚决不防水 还跟我说 我的实验状态很危险 这学期再不好好写实验报告的话 就挂我课 我真的是无语 - -
算了 就不在这里吐槽了 人各有志 笔者继续往下写了
从零开始自制实现正则引擎(四)
1、Hopcroft 算法
这部分其实就是简化DFA状态的 我们不难看出 其实之前DFA还是有地方可以简化的 简化的话 不仅可以使我们后面的转移表内存消耗少一些 还会使整个子串匹配的时间匹配少一些 但是需要多做的工作就是 我们需要花时间去切割 - -
个人认为视频里面讲的已经足够好了 下面会带着伪代码 还有讲一些最后实现的细节 有些地方算法没有说但必须要注意的
1、Hopcroft 算法介绍
先把伪代码放上来了
这个算法我不会仔细讲 视频我也反复看了两遍 最后才自己实现出来的 我就用大白话来总览的说一下吧 我们需要做的 刚开始需要按照 是否为接受态 或者非接受态化为两个set
然后对每个set里面的节点 进行ascii码的遍历 看是否每个节点在ascii码的驱动下还是能够维持在相同的状态 这里的状态指的是 比如q0、q1都为非接受态q0在a的驱动下指向了q2(接受态)q1也能在a的驱动下指向任意接受态 例如指向q5或者q6但因为q5、q6都是接受态 所以在a的驱动下q0、q1状态行为是一致的
但是如果q0(非接受态)的b指向了q5(接受态)而q1(非接受态)的b指向了q0或者q3(都是非接受态)或者q1没有指向此时q0与q1的行为不一致 则不能化为同一集合 则划分开来 然后再对每一个集合进行ascii驱动划分直到没有一个集合能被划开 则到最后的最小化DFA就生成了
这个算法的核心就是看 把一些有着相同状态的节点划分在一起 看是否行为一致 如果行为一致的话 则可以把多个节点融合
2、Hopcroft 特殊情况说明
因为一个情况 我没有搞清楚 而导致本来可以三天多就完成的引擎 我做了五天
大家注意一个情况 例如q0没有找到情况指向外部 则q0此时先不属于任何集合 它只属于它自己 必须要划分开来
注意 笔者再写一次q0如果没有找到情况指向外部 则q0此时先不属于任何集合 它只属于它自己
这个特殊情况 是在我花了大概7个小时调试 发现的问题 我一直以为没有任何指针 则说明 它就属于原本被划分的集合 结果发现 原先没有被优化的DFA生成正确 最小化的DFA经常出现错误 找了很久 才发现是这个问题 而且改了半天都不知道哪里错了 到最后各种调试方法都用尽了才发现是这个问题
2、代码实现
我的hopcroft算法实现 归并到DFA类里面去了 我不想再单独写一个hopcroft头文件了 而且这样的话 也方便访问private成员 省了很多麻烦
1、DFA_node.h
#ifndef __DFA_NODE_H__
#define __DFA_NODE_H__
#include <vector>
#include "global.h"
class DFA_node
{
private:
vector<char> next_values;
vector<DFA_node*> next_work_edges;
int id;
bool state;
friend class DFA;
friend class ReTree;
public:
DFA_node(int n,bool init_state = UNACCEPTABLE):next_values(),next_work_edges(),id(n),state(init_state){}
void print_DFA(unordered_set<DFA_node*>& set);
};
#endif // DFA_NODE_H
2、DFA.h
这部分我先删掉了 后面的Hopcroft简化DFA算法 以免大家对这部分产生疑惑 总体来说 确实是不好实现的 但是最关键的判断子集部分我在上面也已经介绍过了 所以已经降低了一部分实现难度了 这部分是最关键的部分 想要自己实现的hxd 自己可以再去好好琢磨琢磨代码是怎么实现的
#ifndef __DFA_H__
#define __DFA_H__
#include <deque>
#include <unordered_set>
#include "dfa_node.h"
#include "nfa.h"
class DFA
{
private:
DFA_node* root;
vector<bool> visit;
int node_cnt;
public:
DFA():root(nullptr),visit(),node_cnt(0) {}
DFA(NFA* NFA):root(nullptr),visit(vector<bool> ((1 << NFA->total_nodes),false)),node_cnt(0) { build_DFA(NFA); }
~DFA() {delete_all_nodes();}
void build_DFA(NFA* NFA);
void print_DFA_routes() const;
void build(NFA_node* node,NFA_node* end);
bool get_e_closure_set(unordered_set<NFA_node*>& set,deque<NFA_node*>& work_list,NFA_node* node,NFA_node* end,int& pos);
void simplify_DFA();
DFA_node* find_next_edge(DFA_node* node,char chr);
void get_all_DFA_nodes(DFA_node* node,unordered_set<DFA_node*>& set,vector<DFA_node*>& total_nodes);
void hopcraft();
bool split(vector<vector<DFA_node*>>& sets,vector<DFA_node*>& set,unordered_map<DFA_node*,int>& map,int pos);
void delete_all_nodes();
friend class ReTree;
};
#endif
3、DFA_node.cpp
#include "dfa_node.h"
#include <unordered_set>
inline void DFA_node::print_DFA(unordered_set<DFA_node*>& set)
{
if(!this || set.find(this) != set.end()) return;
cout << "now_DFA_id: " << id;
//注释部分是 判断是否正确划分到一个子集中
/*cout << ",now_NFA_ids: ";
for(const auto& node: work_list)
cout << node->id << " ";*/
cout << ",state: " << (state == ACCEPTABLE ? "ACCEPTABLE" : "UNACCEPTABLE") << endl;
set.emplace(this);
int size = next_work_edges.size();
cout << "next_DFA_id & cost_chr: ";
for(int i=0;i<size;++i)
cout << next_values[i] << "->" << next_work_edges[i]->id << " ";
cout << "\n" << endl;
for(int i=0;i<size;++i)
next_work_edges[i]->print_DFA(set);
}
4、DFA.cpp
#include "dfa.h"
#include "dfa_node.h"
#include <unordered_set>
inline void DFA::print_DFA_routes() const
{
unordered_set<DFA_node*> set;
cout << "DFA_Print: " <<endl;
cout << "Node_cnt: " << node_cnt << endl;
root->print_DFA(set);
}
inline void DFA::build_DFA(NFA* NFA)
{
build(NFA->start,NFA->end);
simplify_DFA();
}
inline void DFA::build(NFA_node* start,NFA_node* end)
{
deque<DFA_node*> work_lists{};
deque<NFA_node*> work_list{},tmp{};
deque<deque<NFA_node*>> next_work_lists{};
unordered_set<NFA_node*> set;
unordered_map<int,DFA_node*> cnt;
int pos = 0,nodes = 0,id_max = 0;
bool state = get_e_closure_set(set,tmp,start,end,pos);
if(!tmp.empty())
{
auto node = new DFA_node(id_max++,state);
work_lists.emplace_back(node);
next_work_lists.emplace_back(tmp);
root = node;
visit[pos] = true;
cnt[pos] = node;
++nodes;
}
while(!work_lists.empty())
{
auto now_node = work_lists.front();
work_lists.pop_front();
work_list = next_work_lists.front();
next_work_lists.pop_front();
tmp.clear();
set.clear();
for(int i=1;i<256;++i) // epsilon的情况不考虑进去 因为此时加入epsilon 全为此时工作集的
{
pos = 0;
state = false;
for(const auto& ptr:work_list)
{
if(ptr->value != i) continue;
if(ptr->edge1) state |= get_e_closure_set(set,tmp,ptr->edge1,end,pos);
if(ptr->edge2) state |= get_e_closure_set(set,tmp,ptr->edge2,end,pos);
}
if(!tmp.empty())
{
DFA_node* node = nullptr;
if(visit[pos]) node = cnt[pos];
else
{
node = new DFA_node(id_max++,state);
visit[pos] = true;
cnt[pos] = node;
work_lists.emplace_back(node);
next_work_lists.emplace_back(tmp);
++nodes;
}
now_node->next_values.emplace_back(static_cast<char>(i));
now_node->next_work_edges.emplace_back(node);
tmp.erase(tmp.begin(),tmp.end());
set.clear();
}
}
}
node_cnt = id_max;
}
inline bool DFA::get_e_closure_set(unordered_set<NFA_node*>& set,deque<NFA_node*>& work_list,NFA_node* node,NFA_node* end,int& pos)
{
if(!node) return false;
bool acceptable_state = false;
deque<NFA_node*> tmp{node};
while(!tmp.empty())
{
auto ptr = tmp.front();
tmp.pop_front();
if(set.find(ptr) != set.end()) continue;
if(!ptr->value)
{
if(ptr->edge1) tmp.emplace_back(ptr->edge1);
if(ptr->edge2) tmp.emplace_back(ptr->edge2);
}
work_list.emplace_back(ptr);
pos |= (1 << ptr->id);
set.emplace(ptr);
if(ptr == end)
acceptable_state = true;
}
return acceptable_state;
}
inline void DFA::simplify_DFA()
{
hopcraft();
}
inline DFA_node* DFA::find_next_edge(DFA_node* node,char chr)
{
if(node->next_values.empty()) return nullptr;
int size = node->next_values.size();
for(int i=0;i<size;++i)
{
auto tmp = node->next_values[i];
if(tmp == chr)
return node->next_work_edges[i];
}
return nullptr;
}
inline bool DFA::split(vector<vector<DFA_node*>>& sets,vector<DFA_node*>& set,unordered_map<DFA_node*,int>& map,int pos)
{
if(set.size() <= 1) return false;
unordered_map<int,vector<DFA_node*>> DFA_map;
unordered_set<int> id_set;
int id_first = 0,new_id = -256;
for(int i=1;i<256;++i)
{
auto chr = static_cast<char>(i);
for(const auto& node:set)
{
auto next_ptr = find_next_edge(node,chr);
int tmp_pos = (next_ptr ? map[next_ptr] : map[node]);
if(node->next_values.empty()) //因为没有边链接 所以属于单独的状态
{
tmp_pos = new_id;
map[node] = new_id;
++new_id;
}
id_set.emplace(tmp_pos);
}
if(id_set.size() != 1)
{
id_set.clear();
for(const auto& node:set)
{
auto next_ptr = find_next_edge(node,chr);
int pos = (next_ptr ? map[next_ptr] : map[node]);
id_set.emplace(pos);
DFA_map[pos].emplace_back(node);
}
for(const auto& num:id_set)
{
if(id_first == 0)
{
sets[pos] = DFA_map[num];
id_first = 1;
for(const auto& node:DFA_map[num])
map[node] = pos;
}
else
{
sets.emplace_back(DFA_map[num]);
int now_size = sets.size() - 1;
for(const auto& node:DFA_map[num])
map[node] = now_size;
}
}
return true;
}
id_set.clear();
}
return false;
}
inline void DFA::get_all_DFA_nodes(DFA_node* node,unordered_set<DFA_node*>& set,vector<DFA_node*>& total_nodes)
{
if(!node || set.find(node) != set.end())
return;
set.emplace(node);
total_nodes.emplace_back(node);
for(const auto& ptr:node->next_work_edges)
{
if(set.find(ptr) == set.end())
get_all_DFA_nodes(ptr,set,total_nodes);
}
return;
}
inline void DFA::hopcraft()
{
if(!root) return;
bool can_be_split = true;
vector<vector<DFA_node*>> sets(2,vector<DFA_node*>());
vector<DFA_node*> total_nodes;
unordered_set<DFA_node*> set;
unordered_map<DFA_node*,int> map;
get_all_DFA_nodes(root,set,total_nodes);
for(const auto& node:total_nodes)
{
int num = (node->state == ACCEPTABLE);
sets[num].emplace_back(node);
map[node] = num;
}
while(can_be_split)
{
can_be_split = false;
int size = sets.size();
for(int i=0;i<size;++i)
{
if(sets[i].empty()) continue;
can_be_split = split(sets,sets[i],map,i);
if(can_be_split) break;
}
}
int root_id = map[root];
/*for(const auto& set:sets)
{
cout << "id: " ;
for(const auto& node:set)
{
cout << node->id << ' ';
}
cout << endl;
}*/
unordered_set<char> chr_set;
unordered_set<int> work_id_set;
unordered_map<int,DFA_node*> node_map;
deque<DFA_node*> work_list;
deque<int> work_id;
int id_max = 0;
if(map.find(root) != map.end())
{
auto node = new DFA_node(id_max++);
root = node;
work_list.emplace_back(node);
work_id.emplace_back(root_id);
}
while(!work_list.empty())
{
chr_set.clear();
auto now_node = work_list.front();
work_list.pop_front();
int id = work_id.front();
work_id.pop_front();
for(auto& node:sets[id])
{
if(node->state == ACCEPTABLE) now_node->state = ACCEPTABLE;
int size = node->next_values.size();
for(int i=0;i<size;++i)
{
char chr = node->next_values[i];
if(chr_set.find(chr) == chr_set.end())
{
chr_set.emplace(chr);
int node_id = map[node->next_work_edges[i]];
DFA_node* ptr = nullptr;
if(node_map.find(node_id) != node_map.end()) ptr = node_map[node_id];
else
{
ptr = new DFA_node(id_max++);
node_map[node_id] = ptr;
}
now_node->next_values.emplace_back(chr);
now_node->next_work_edges.emplace_back(ptr);
if(work_id_set.find(node_id) == work_id_set.end())
{
work_list.emplace_back(ptr);
work_id.emplace_back(node_id);
work_id_set.emplace(node_id);
}
}
}
}
}
for(auto& node:total_nodes)
free(node);
node_cnt = id_max;
}
inline void DFA::delete_all_nodes()
{
if(!root) return;
unordered_set<DFA_node*> set;
vector<DFA_node*> total_nodes;
get_all_DFA_nodes(root,set,total_nodes);
for(const auto& node:set)
delete(node);
}
3、验证DFA最小化生成正确
做这个之前一定要多次验证自己的DFA是否生成正确 如果基本的DFA都没有生成正确 那你如何把后背交给一个没有生成正确的DFA 在此之上 头朝着天空 坠落到基础DFA用手连起来的保护网上呢
所以在此之前一定要多次验证DFA生成的正确性
1、验证结果1(生成正确)
表达式用的和上篇博客的一样
表达式ac*|aa|bb|cc无法作优化 已经是最优解了

2、验证结果2(验证正确)
表达式|a 还是没法优化 - - 优化了反而是错的

3、验证结果3(验证正确)
表达式ac(b*)|(a)(bb*)cc
这个相较于之前的 优化了两个节点 验证了一下 确实是对的
后面再验证一个吧 其实私底下我已经验证过很多个了 不验证的话 我自己也不会跑出来写博客了 哈哈

4、验证结果4(验证正确)
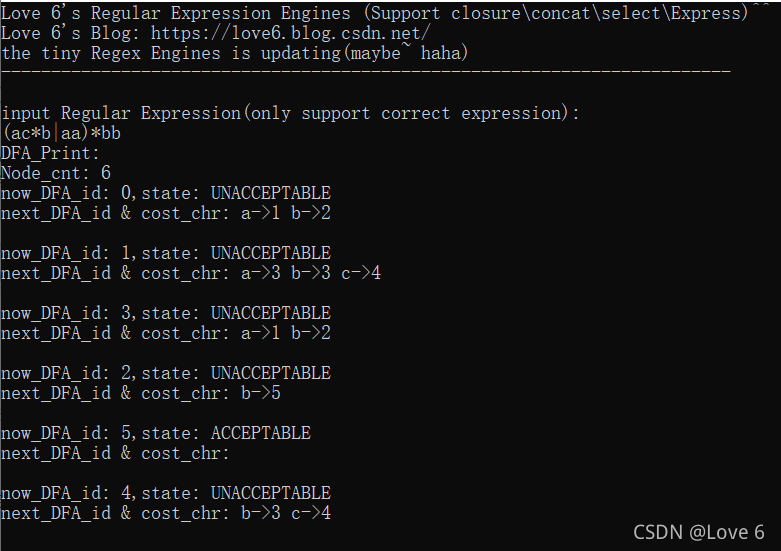
表达式(ac*b|aa)*bb
自己动手画了一下 比较复杂 但是是对的 哈哈 之前放很少的图就是因为后面的最终结果是对的 那么之前的结果那也肯定是对的 只是因为人懒 就没放了 但不代表我没认真的调试过哈 哈哈 最后一篇再见啦~




























 265
265

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










