堆排序优化

此篇是在上一篇文章堆排序进行展开讨论的。

一，概要

在上一遍中，在向一个完全二叉堆中添加数据时，是将数组的每一个元素一一插入，插入堆的元素还需要判断其位置是否合理，通过下列方法可以只对插入的元素的一半进行判断操作。

二，方法

找到第后一个有孩子的结点，判断此结点的位置的值对于它的孩子来说，是不是合理的，然后从此结点开始，向前依次判断每一个结点，直到根结点。

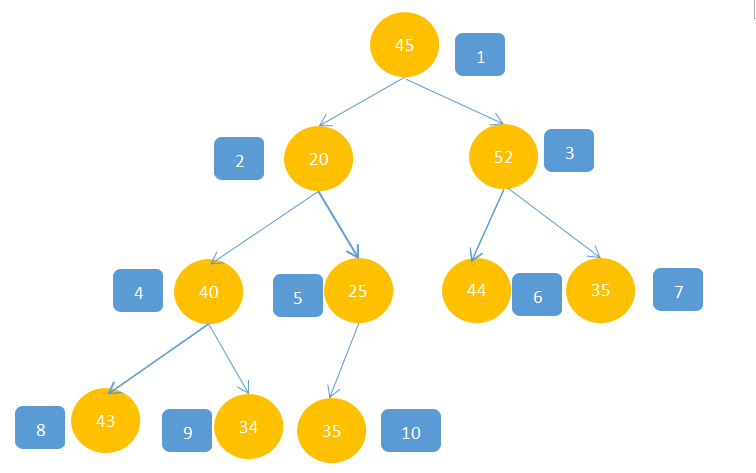
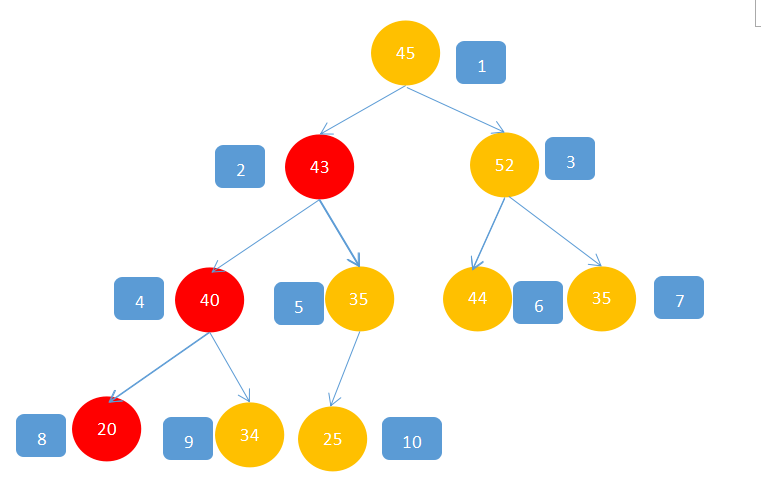
对于如图：堆，显然不满足最大堆的性质；

方法步骤：

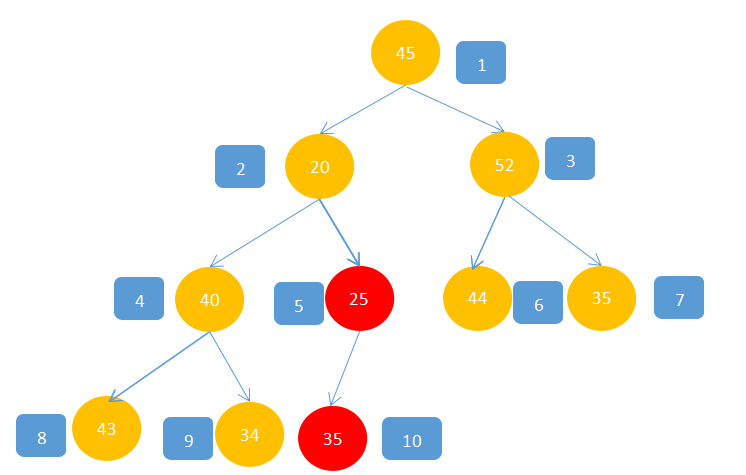
1，找到第后一个有孩子的结点，观察图会发现，只需用最后一个结点除以2，就可以找到，如图中：10/2=5；找到5这个结点，接下来就是要判断5这个位置的值合不合理，显然35>25,不满足最大堆，所以35与25交换：

2,此时5这个结点相对于它孩子已经满足了最大堆性质，接下来，移动到5的上一个结点4，显然4，这个位置的值不满足，所以要对其进行操作，40>34,40<43,所以40与43交换。

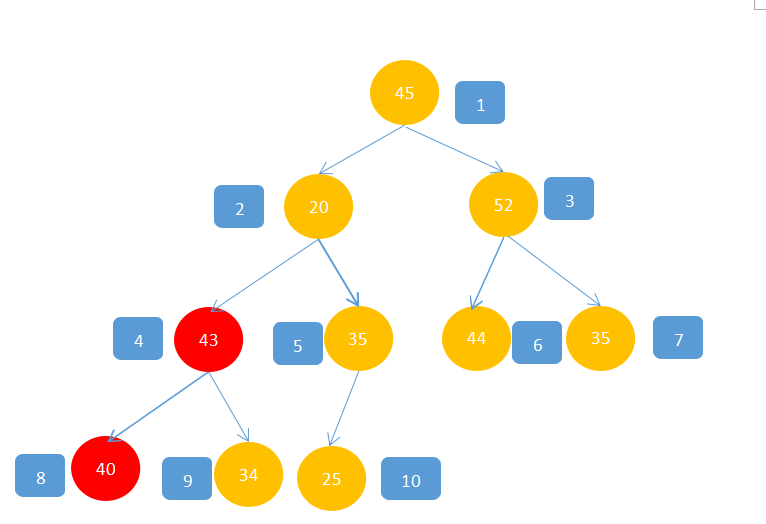
3，此时在移动到下一个结点3，已经满足，不做操作；

4，移动到2，不满足，20<43,20<35,所以43与20交换。

5，此时发现20所在的位置还不满足，所以继续判断，20<40,20<34,所以20与40交换。

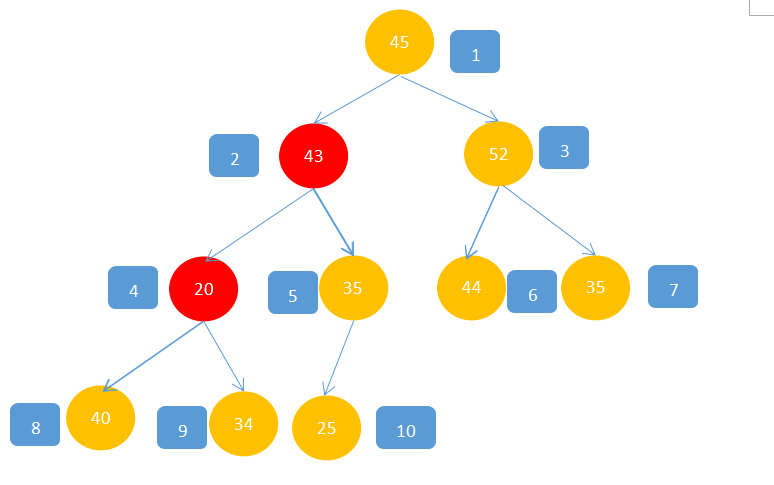
6，最后移动到最后一个结点，45<52,45>43,所以52与45交换。

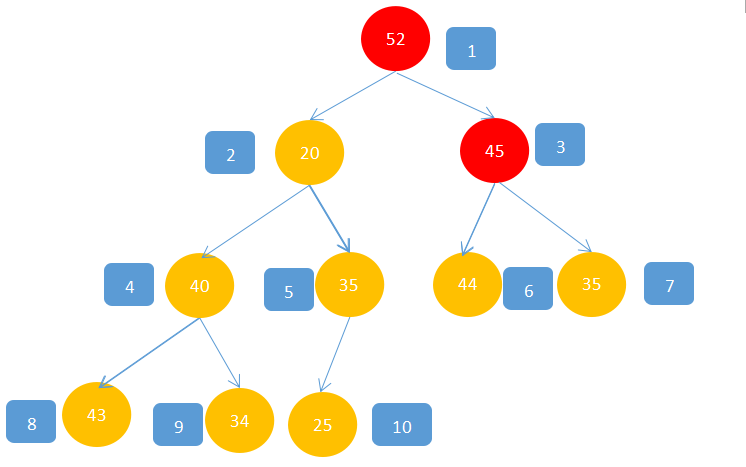
这样就完成将一个数组构建成二叉对的过程。

代码实现：

在之前的代码基础上加上一个构造函数：

//传入一个数组arr，数组个数n,以及堆容量 capacity
MaxHeap::MaxHeap(int arr[],int n,int capacity)
{
	data = new int[capacity];
	for (int i = 1; i <=n; i++)
		data[i] = arr[i];
	this->capacity = capacity;
	count = n;

	for (int j = n / 2; j > 0; j--) {
		shiftDown(j);//其实就是对每个节点进行shiftdown
	}

}

三，对比：

通过上述步骤可以发现，我们并没有对5结点之后的，6,7,8,9,10，进行判断，相比于普通的方法，此方法明显提高了一定的效率。（插入几个数，不会用什么影响，但是单数据量大的时候，比如1000000，通过优化只要对前500000进行判断操作，效率肯定能大大提升），小面通过代码来对比。

代码：

#include<iostream>
#include"HeapSort.h"
#include<ctime>
#include<string>
using namespace std;


//生成n个的随机数组，，每个元素的范围{RangeL，RangeR}
int * generateRandromArray(int n, int rangel, int rangeR) {
	int *arr = new int[n];
	srand(time(0));
	for (int i = 0; i < n; i++) {
		arr[i] = rand() % (rangeR - rangel + 1) + rangel + 1;
	}

	return arr;
}

//数组赋值
int * copyArray(int arr[], int n) {
	int * temp = new int[n];
	for (int i = 0; i < n; i++)
		temp[i] = arr[i];
	return temp;
}

//用于测试排序所用时间
void testSort(string sortName, void(*sort)(int[], int n), int arr[], int n) {
	clock_t startTime = clock();
	sort(arr, n);
	clock_t endTime = clock();
	cout << sortName << ":" << double(endTime - startTime) / CLOCKS_PER_SEC << " s" << endl;
}

//普通构建堆方法
void sort1(int arr[], int n) {
	MaxHeap maxheap= MaxHeap(n+1);//创建堆
	for (int i = 0; i <n; i++)
	{
		maxheap.insert(arr[i]);
	}

}
//第二种方法
void sort2(int arr[], int n) {
	MaxHeap maxheap1 = MaxHeap(arr, n, n+1);//创建堆
}

int main() {
	int n = 1000000;
	int *arr = generateRandromArray(n, 0, n);//生成随机数组
	int *arr1;
	//复制数组
	arr1 = copyArray(arr, n);

	testSort("sort1 :", sort1, arr, n);
	testSort("sort2 :", sort2, arr1, n);

	return 0;
}

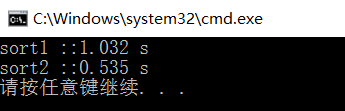
运行结果：

可以发现第二种方法比普通方法快一倍！

总结：认真领悟：