线性方程组的SOR迭代法

写在前面

• 1 SOR简介
• 2 SOR算法推导
• 3 SOR算法收敛性
• 4 实例分析
• 5 代码实现
• 6 参考文献与链接

迭代法收敛定理

定理1(充要条件)：
矩阵$\mathbf{M}$的谱半径
ρ ( M ) = max ⁡ i { λ i ∣ i = 1 , 2 , ⋯ n } < 1 ( ∥ M ∥ 2 < 1 )    (1) \rho \left( \mathbf{M} \right) =\mathop {\max} \limits_i\left\{ \lambda _i\left| i=1,2,\cdots n \right. \right\} <1\left( \lVert \mathbf{M} \rVert _2<1 \right) \,\, \tag{1} ρ(M)=imax​{λi​∣i=1,2,⋯n}<1(∥M∥2​<1)(1)

定理2(充分条件)：
矩阵$\mathbf{M}$的某个算子范数
$$\Vert \mathbf{M}\Vert <1\text{\hspace{1em}(2)}$$

1 SOR简介

SOR是Successive Over Relaxation（逐次超松弛）的缩写。该方法是求解大型稀疏矩阵方程组的有效方法之一，也可看作为Gauss-Seidel迭代法的加速，Gauss-Seidel是SOR迭代的一种特殊形式。

2 SOR算法推导

将方程组$\mathbf{A}\mathbf{X}=b$写成
$$a_{i1}{x}_1+a_{i2}{x}_2+\cdots +a_{i,i-1}{x}_{i-1}+a_{ii}{x}_i\cdots +a_{in}{x}_n=b_i,(i=1,2,\cdots ,n)\text{\hspace{1em}(2.1)}$$
则
$$\begin{array}{rl}& \Rightarrow a_{ii}{x}_i=b_i-\left(a_{i1}{x}_1+a_{i2}{x}_2+\cdots +a_{i,i-1}{x}_{i-1}\right)-\left(a_{i,i+1}{x}_{i+1}+\cdots +a_{in}{x}_n\right)\\ & \Rightarrow a_{ii}{x}_i=a_{ii}{x}_i+\left(b_i-a_{i1}{x}_1-a_{i2}{x}_2-\cdots -a_{i,i-1}{x}_{i-1}-a_{ii}{x}_i-a_{i,i+1}{x}_{i+1}-\cdots -a_{in}{x}_n\right)\\ & \Rightarrow x_i=x_i+\frac{1}{a_{ii}}\left(b_i-a_{i1}{x}_1-a_{i2}{x}_2-\cdots -a_{i,i-1}{x}_{i-1}-a_{it}{x}_i-a_{i,i+1}{x}_{i+1}-\cdots -a_{in}{x}_n\right)\end{array}$$
于是Gauss-Seidel迭代法可写成（$a_{i,i}\ne 0$）
$$\begin{array}{c}{x}_i^{(k+1)}=x_i^{(k)}+\frac{1}{a_{ii}}\left(b_i-a_{i1}{x}_1^{(k+1)}-\cdots -a_{i,i-1}{x}_{i-1}^{(k+1)}-a_{in}{x}_i^{(k)}-\cdots -a_{in}{x}_n^{(k)}\right)\\ =x_i^{(k)}+\frac{1}{a_{ii}}\left(b_i-{\sum }_{j=1}^{i-1}{a}_{ij}{x}_j^{(k+1)}-{\sum }_{j=i}^n{a}_{ij}{x}_j^{(k)}\right)\\ r_i^{(k)}=\left(b_i-{\sum }_{j=1}^{i-1}{a}_{ij}{x}_j^{(k+1)}-{\sum }_{j=i}^n{a}_{ij}{x}_j^{(k)}\right),i=1,2,\cdots ,n\end{array}\text{\hspace{1em}(2.2)}$$
记
$$r_i^{(k)}=\left(b_i-\sum _{j=1}^{i-1}{a}_{ij}{x}_j^{(k+1)}-\sum _{j=i}^n{a}_{ij}{x}_j^{(k)}\right),i=1,2,\cdots ,n$$
则(2.2)式可写成
$$x_i^{(k+1)}=x_i^{(k)}+\frac{1}{a_{ii}}{r}_i^{(k)}\text{\hspace{1em}(2.3)}$$
由(2.3)式可看出，Gauss-Seidel迭代法的第$k+1$步的基础上每个分量上加上$\frac{1}{a_{ii}}{r}_i^{(k)}$。为了获得更快的收敛效果，在修正项的前面乘以一个参数$\omega$，于是得到逐次超松弛算法
$$x_i^{(k+1)}=x_i^{(k)}+\frac{\omega }{a_{ii}}{r}_i^{(k)},i=1,2,\cdots ,n\text{\hspace{1em}(2.4)}$$
即
$$x_i^{(k+1)}=(1-\omega )x_i^{(k)}+\frac{\omega }{a_{ii}}\left(b_i-\sum _{j=1}^{i-1}{a}_{ij}{x}_j^{(k+1)}-\sum _{j=i+1}^n{a}_{ij}{x}_j^{(k)}\right),i=1,2,\cdots ,n\text{\hspace{1em}(2.5)}$$
其矩阵形式为
$${\mathbf{X}}^{(k+1)}=(1-\omega ){\mathbf{X}}^{(k)}+\omega {\mathbf{D}}^{-1}\left(b+\mathbf{L}{\mathbf{X}}^{(k)}+\mathbf{U}{\mathbf{X}}^{(k)}\right)\text{\hspace{1em}(2.6)}$$
其中，$\mathbf{A}=\mathbf{D}-\mathbf{L}-\mathbf{U}$
$$\mathbf{D}=\left(\begin{array}{cccc}{a}_{11}& & & \\ & a_{22}& & \\ & & \ddots & \\ & & & a_{nn}\end{array}\right),\mathbf{L}=\left(\begin{array}{cccc}0& & & \\ a_{21}& 0& & \\ ⋮& \ddots & \ddots & \\ a_{n1}& a_{n2}& \cdots & 0\end{array}\right),\mathbf{U}=\left(\begin{array}{cccc}0& a_{12}& \cdots & a_{1n}\\ & 0& \ddots & a_{2n}\\ & & \ddots & ⋮\\ & & & 0\end{array}\right)$$

3 SOR算法收敛性

由(2.6)式有
$${\mathbf{D}\mathbf{X}}^{\left(k+1\right)}=\left(1-\omega \right){\mathbf{D}\mathbf{X}}^{\left(k\right)}+\omega \left(b+{\mathbf{L}\mathbf{X}}^{\left(k+1\right)}+{\mathbf{U}\mathbf{X}}^{\left(k\right)}\right)$$
即
$$\mathbf{D}{\mathbf{X}}^{(k+1)}-\omega \mathbf{L}{\mathbf{X}}^{(k+1)}=(1-\omega )\mathbf{D}{\mathbf{X}}^{(k)}+\omega \mathbf{U}{\mathbf{X}}^{(k)}+\omega b$$
于是有
$$\begin{array}{l}(\mathbf{D}-\omega \mathbf{L}){\mathbf{X}}^{(k+1)}=[(1-\omega )\mathbf{D}+\omega \mathbf{U}]{\mathbf{X}}^{(k)}+\omega b\\ \Rightarrow {\mathbf{X}}^{(k+1)}=(\mathbf{D}-\omega \mathbf{L}{)}^{-1}[(1-\omega )\mathbf{D}+\omega \mathbf{U}]{\mathbf{X}}^{(k)}+\omega (\mathbf{D}-\omega \mathbf{L}{)}^{-1}b\end{array}$$
记
$$\{\begin{array}{c}{\mathbf{B}}_{\omega }=(\mathbf{D}-\omega \mathbf{L}{)}^{-1}[(1-\omega )\mathbf{D}+\omega \mathbf{U}]\\ {\mathbf{F}}_{\omega }=\omega (\mathbf{D}-\omega \mathbf{L}{)}^{-1}b\end{array}\text{\hspace{1em}(3.1)}$$
则有
$${\mathbf{X}}^{(k+1)}={\mathbf{B}}_{\omega }(X{)}^{(k)}+{\mathbf{F}}_{\omega }\text{\hspace{1em}(3.2)}$$
其中，${\mathbf{B}}_{\omega }$为SOR迭代矩阵。
由收敛定理的定理1和定理2可知，SOR收敛的充要条件是$\rho ({\mathbf{B}}_{\omega })<1$或者$\Vert {\mathbf{B}}_{\omega }{\Vert }_2<1$，可以看出SOR迭代法收敛与否或收敛的快慢都与松弛因子$\omega$有关，因此SOR迭代算法存在如下定理.
定理3: SOR迭代法收敛的充要条件是松弛因子$0<\omega <2$ .
证：由于SOR收敛，则$\rho ({\mathbf{B}}_{\omega })<1$。记${\mathbf{B}}_{\omega }$的特征值为${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$,而$n$阶矩阵的$n$个特征值之积等于其行列式之值，即
$$\left|\det {\mathbf{B}}_{\omega }\right|=\left|{\lambda }_1{\lambda }_2\cdots {\lambda }_n\right|$$
而
$$\left|{\lambda }_i\right|\le \left|\rho \left({\mathbf{B}}_{\omega }\right)\right|$$
故
$$\left|\det {\mathbf{B}}_{\omega }\right|=\left|{\lambda }_1{\lambda }_2\cdots {\lambda }_n\right|\le {\left[\rho \left({\mathbf{B}}_{\omega }\right)\right]}^n<1$$
另一方面，由
$${\mathbf{B}}_{\omega }=(\mathbf{D}-\omega \mathbf{L}{)}^{-1}[(1-\omega )\mathbf{D}+\omega \mathbf{U}]$$
有
$$\left|\det {\mathbf{B}}_{\omega }\right|=\left|\det (\mathbf{D}-\omega \mathbf{L}{)}^{-1}\right|\cdot |\det [(1-\omega )\mathbf{D}+\omega \mathbf{U}]$$
即
$$\left|\det {\mathbf{B}}_{\omega }\right|=\frac{|\det [(1-\omega )\mathbf{D}+\omega \mathbf{U}]|}{|\det (\mathbf{D}-\omega \mathbf{L})|}=|1-\omega {|}^n$$
因此有$|1-\omega {|}^n<1$或者$|1-\omega |<1$,也即$0<\omega <2$.　　　　　　　　　　　$\square$

定理4：如果矩阵$\mathbf{A}$是对称正定的，则SOR法对于$0<\omega <2$是收敛的。

4 实例分析

用逐次超松弛（SOR）迭代法求解方程组$\mathbf{A}\mathbf{X}=b$，其中矩阵$\mathbf{A}$为
$$\mathbf{A}=\left[\begin{array}{ccccccc}12& -2& 1& & & & \\ -2& 12& -2& 1& & & \\ 1& -2& 12& -2& 1& & \\ & \ddots & \ddots & \ddots & \ddots & \ddots & \\ & & 1& -2& 12& -2& 1\\ & & & 1& -2& 12& -2\\ & & & & 1& -2& 12\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ ⋮\\ x_{18}\\ x_{19}\\ x_{20}\end{array}\right]=\left[\begin{array}{c}5\\ 5\\ 5\\ ⋮\\ 5\\ 5\\ 5\end{array}\right]\text{\hspace{1em}(4.1)}$$
利用Matlab2016a软件求解(4.1)式（具体程序见第五节），讨论不同的松弛因子$\omega$对迭代速度的影响。其中参数设置为：最大迭代值为500。

由于(4.1)式是一个对称正定阵，且本文规定松弛因子$0<\omega <2$，因此由定理4可知，式(4.1)一定收敛，也即有解。求解的结果如下表。

表1　不同 $\omega$值对方程收敛速度的影响

w	迭代次数
0.3	120
0.6	50
0.9	25
1.2	30
1.5	50
1.8	150

.

图1 不同$\omega$值时的SOR迭代曲线值
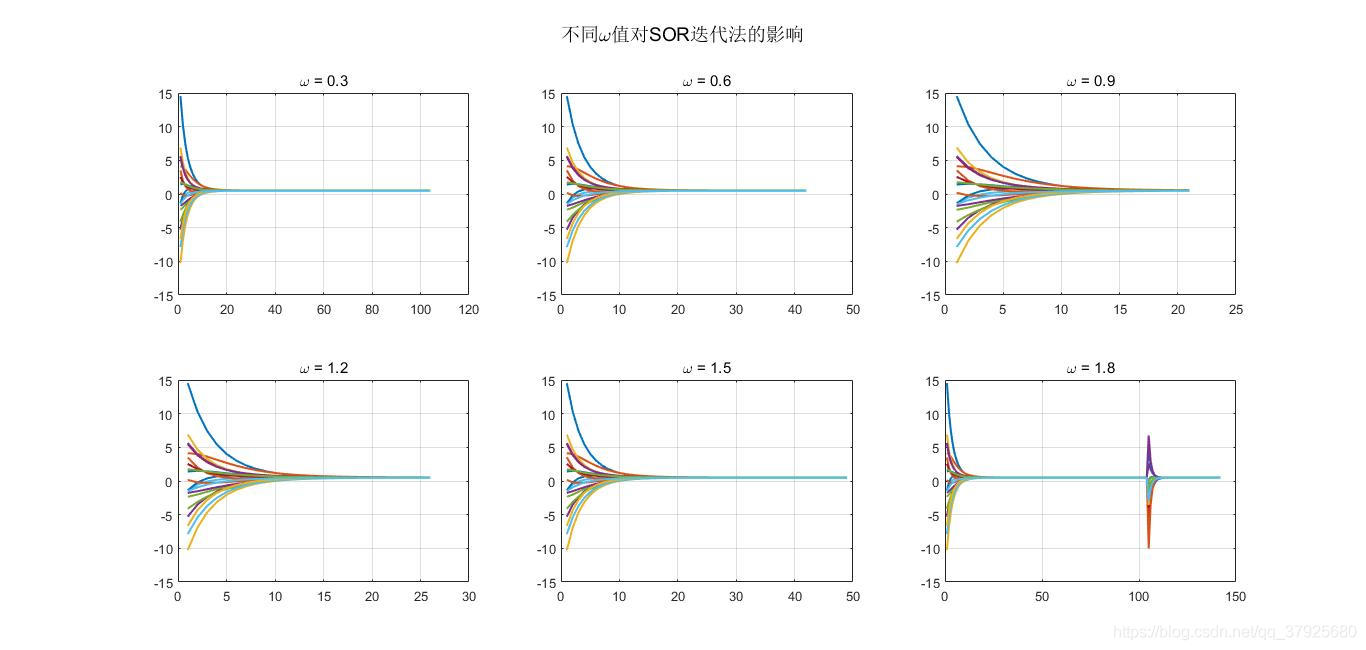
由表1或图1可知，（1）当SOR迭代法松弛因子 $\omega >1$时， $\omega$值越大，迭代的次数就越多，收敛速度就越慢， $\omega$越接近1时，迭代的次数越少，收敛速度越快；（2）当SOR迭代法松弛因子 $\omega <1$时， $\omega$越小，迭代的次数就越多，收敛速度就越慢， $\omega$越接近1时，迭代的次数越少，收敛速度越快；（3）SOR迭代法松弛因子不在范围内时，系数矩阵的谱半径大于1，不收敛。

小结

1. 在SOR迭代算法中，松弛因子$\omega$越接近1时，迭代的次数越小，收敛速度越快，故$\omega$最优值应选择$\omega =1$。
2. 在SOR迭代算法中，松弛因子$\omega$距离1越远时，迭代次数越多，收敛速度越慢。
3. 在SOR迭代算法中，松弛因子应选择$0<\omega <2$，当$\omega$超过这个范围时，不满足收敛定理，即谱半径不小于1，此时方程无解。

5 代码实现

close all;clear;clc;%清空环境变量
load('A.mat');%导入矩阵A
b=5*ones(20,1);%导入矩阵b
D=diag(diag(A));%求解对角阵
LA=tril(A);%抽取下三角矩阵
U=LA-A;%得到去除对角线元素的上三角阵
L=D-LA;%得到去除对角线元素的下三角阵
XXX=[];%存储不同松弛因子的迭代值
I=[];%记录迭代终止次数
for w=0.3:0.3:2;%设置松弛因子大小0<w<2
    XX=[];
    %% SOR迭代公式
    M=(D-w*L)\((1-w)*D+w*U);
    f=w*((D-w*L)\b);
    MaxEigM = max(abs(eig(M)));%求谱半径
    x=[];
    x(:,1)=5.*randn(size(b));%给出任意的迭代初始值
    N=500;%最大迭代次数
    %% 如果谱半径小于1则说明收敛，否则不收敛    
    if MaxEigM<1
        i=1;        
        while i<N
            if norm(A*x(:,i)-b)>=1e-10;
                x(:,i+1)=M*x(:,i)+f;
                z=x(:,i+1);
                i=i+1;                              
            else
                n=i;
                z=x(:,i);
                i=N;
            end
        end
        XX=[XX,x];
        I=[I length(XX)];
        XXX=[XXX XX];
        e=norm(A*z-b);       
    else
        out='谱半径大于等于1，该方程不能用SOR方法求解'
    end
end
%% 绘图
subplot(2,3,1)
plot(1:I(1,1),XXX(:,1:I(1,1)),'linewidth',1.5)
grid on
title('\omega = 0.3')
subplot(2,3,2)
plot(1:I(1,2),XXX(:,1:I(1,2)),'linewidth',1.5)
grid on
title('\omega = 0.6')
subplot(2,3,3)
plot(1:I(1,3),XXX(:,1:I(1,3)),'linewidth',1.5)
grid on
title('\omega = 0.9')
subplot(2,3,4)
plot(1:I(1,4),XXX(:,1:I(1,4)),'linewidth',1.5)
grid on
title('\omega = 1.2')
subplot(2,3,5)
plot(1:I(1,5),XXX(:,1:I(1,5)),'linewidth',1.5)
grid on
title('\omega = 1.5')
subplot(2,3,6)
plot(1:I(1,6),XXX(:,1:I(1,6)),'linewidth',1.5)
grid on
title('\omega = 1.8')
suptitle('不同\omega值对SOR迭代法的影响')

数据下载地址
可关注微信公众号用数学看世界回复“SOR密码”获取数据下载地址及密码

6 参考文献与链接

[1] 数值分析 曾繁慧
[2] 科学计算与应用软件讲义_迭代思想 胡行华
[3] https://mdnice.com/
[4] Markdown Nice插件下载
[5] Markdown三线表制作方法
为了能够敲公式，第一次使用Markdown写文章，有很多不足之处请谅解
Markdown真香，更多内容请关注公众号获取