深度学习：神经网络-BP算法原理及利用python从零实现

摘要：给出反向传播算法的具体推导，并通过一个例子对反向传播的计算流程进行介绍。最后利用python从零实现一个神经网络。代码仅作为公式的理解，不具备重复使用能力。

目录

1. BP算法原理
2. 简单实例
3. python从零实现
4. 各资料中的BP算法公式

参考

【1】“Neural Networks and Deep Learning”. Michael A. Nielsen.

【2】“Pattern Classification”.

【3】“Neural Networks and Deep Learning”. 邱锡鹏.

1. BP算法原理

有关多层感知器、神经网络的具体内容在各参考文献中均有详细介绍。

对于前馈网络，前向传播接收输入数据$x$，计算输出$\hat{y}$。在训练时通过输出$\hat{y}$计算损失$J(\theta )$。反向传播算法通过计算$J(\theta )$的梯度，允许信息从输出层反向传输，如图1。下面开始介绍反向传播的具体过程，并通过一个例子加深理解。

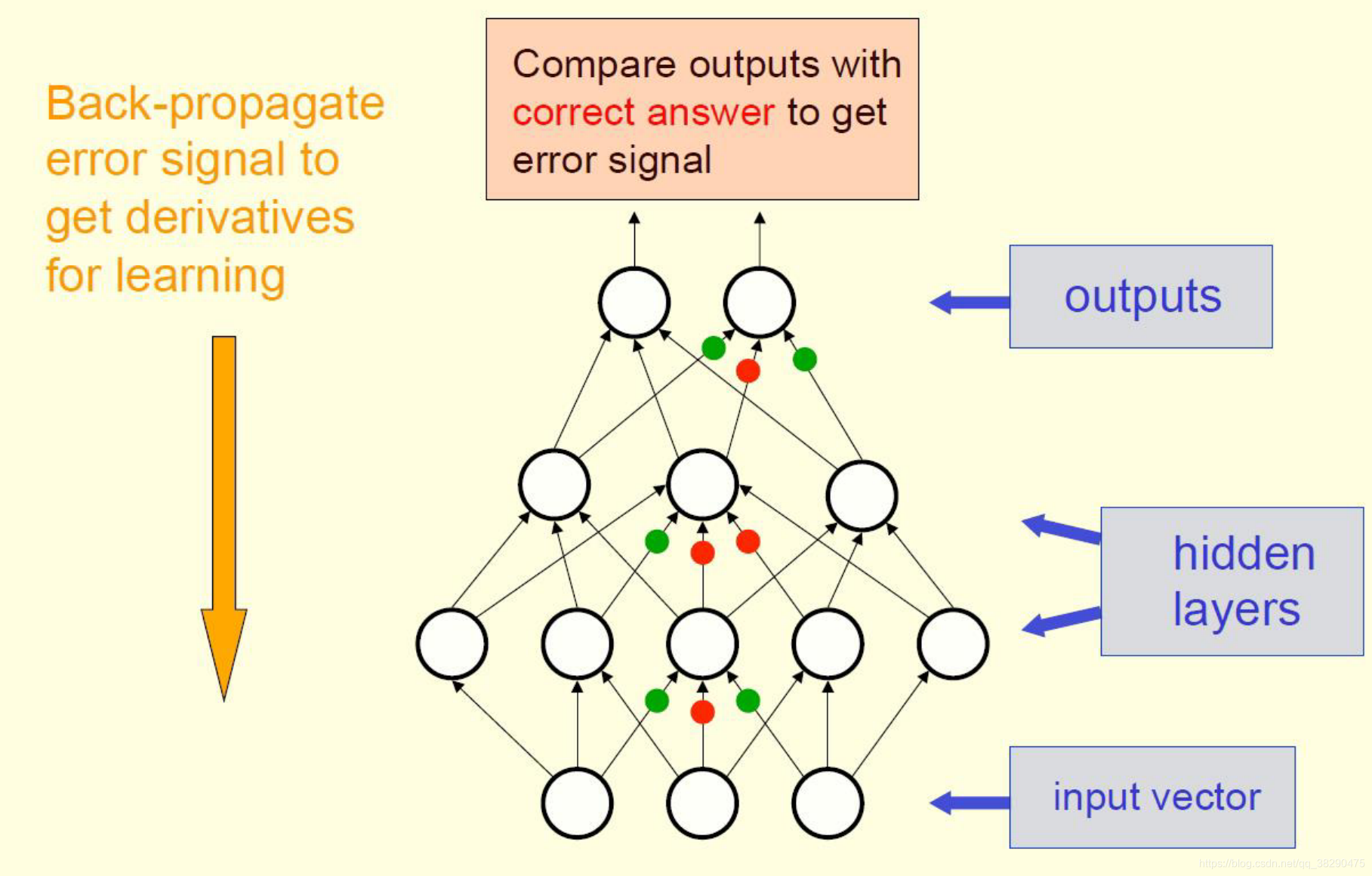
首先给出Hinton报告中的几点说明：

1. 从输入数据，我们并不知道隐层单元时如何工作的；
2. 但我们能知道当隐层激活改变时，损失减少的快慢程度(通过梯度)；
3. 每一个隐层单元能影响多个输出节点，并且对误差有不同的影响；
4. 通过微分链式法则，损失函数每个权重的梯度很容易计算。

接下去就重点分析一下这个很容易计算的过程。

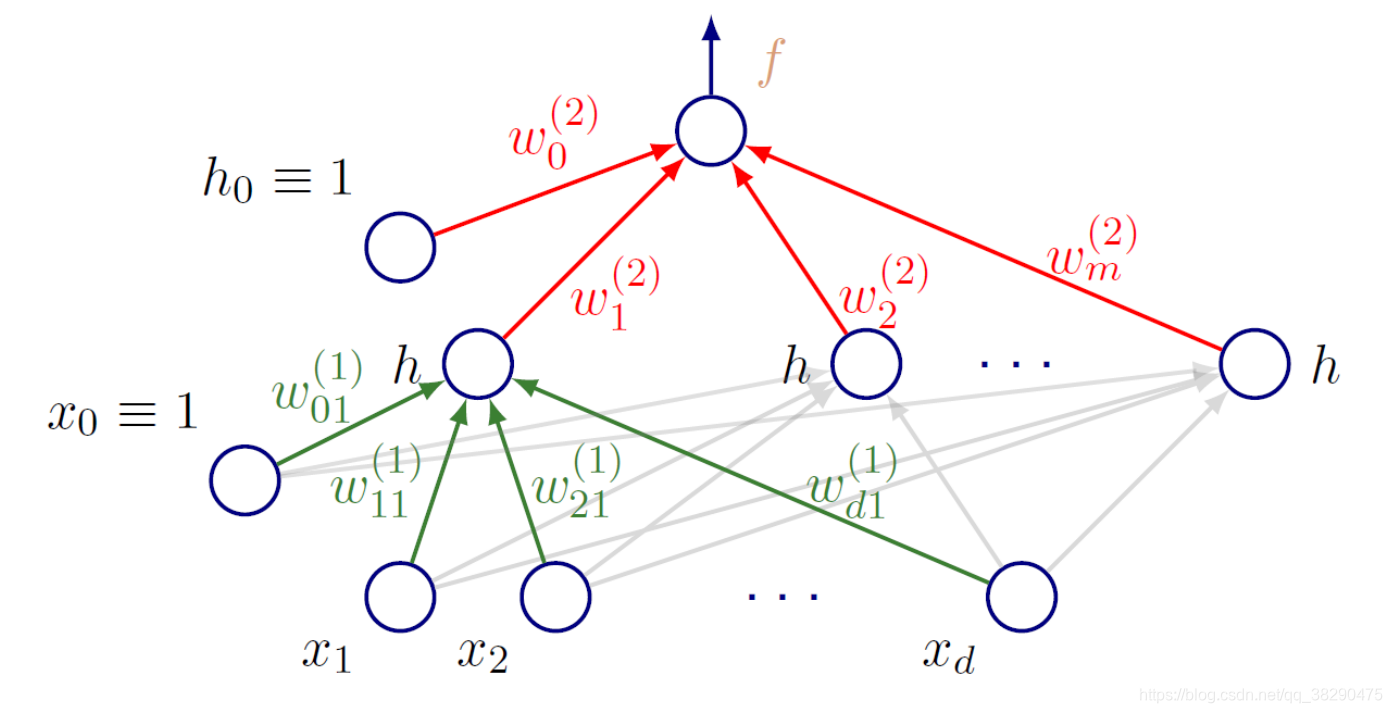
上图即一个常见的全连接网络结构，输入向量$x$有$d$个维度，单隐层有$m个单元$，单输出模型，并且包括下标为$0$的偏置项。

根据前向操作，从输入$x$到输出$\hat{y}$，我们有如下公式：

$$\hat{y}(x;w)=f\left(\sum _{j=1}^m{w}_j^{(2)}h\left(\sum _{i=1}^d{w}_{ij}^{(1)}{x}_i+w_{0j}^{(1)}\right)+w_0^{(2)}\right)$$

公式即简单的线性操作加非线性激活，再进行线性操作和非线性激活，就得到估计的输出。

网络的误差同样很容易得到：

$$L(X;w)=\sum _{i=1}^M\frac{1}{2}{\left(y_i-\hat{y}(x;w)\right)}^2$$

这里用的就是常见的平方损失。

通常，由于非线性激活的存在，最小化上述误差都是没有闭式解的，因此需要用到梯度下降等优化算法。并且对每个样本，我们都要计算其梯度。

这里给出一个简单的线性模型：$\hat{y}={\sum }_j{w}_j{x}_{ij}$，作为例子，观察梯度的特点。梯度计算如下：
$$\frac{\partial L(x_i)}{\partial w_j}=({\hat{y}}_i-y)x_{ij}$$
即，梯度为误差乘输入。

对于如下图所示的多层神经网络的特定单元，其有$s$个输入单元，我们分析它所连的第$t$个输出单元。

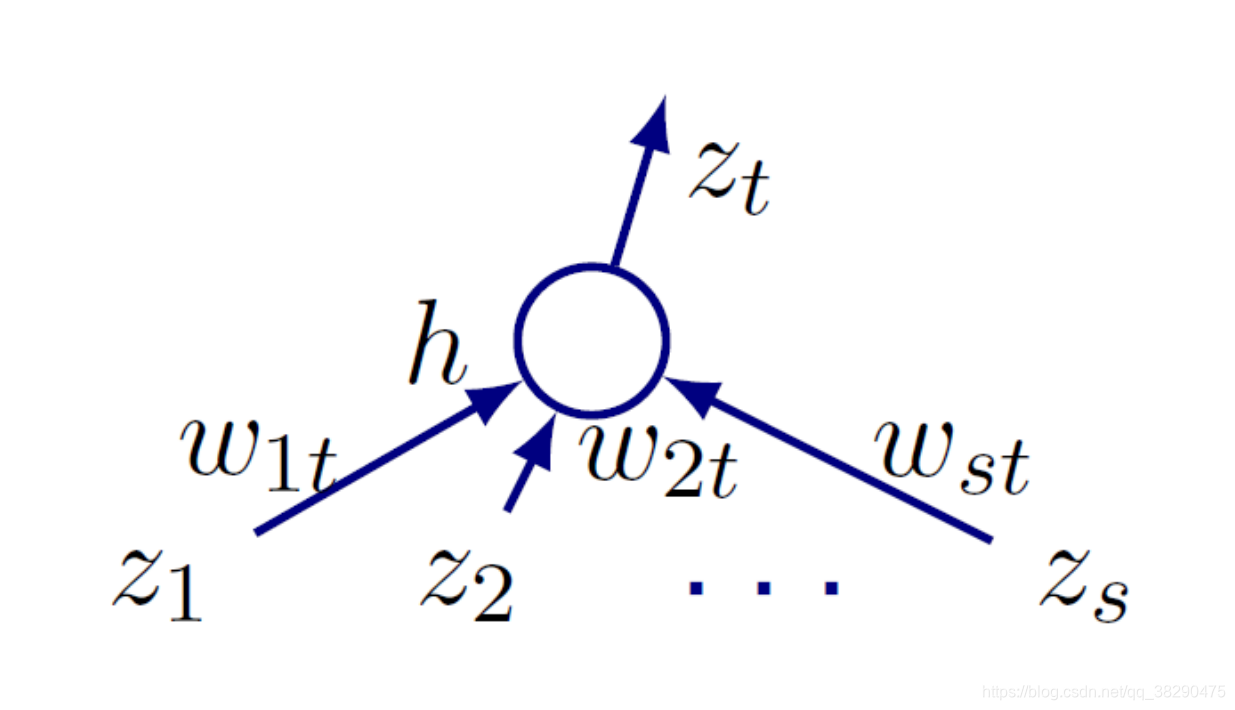
其输出$z_t$可以表示为

$$z_t=h\left(\sum _j{w}_{jt}{z}_j\right)$$

其中，记住我们的$j$是上一层的神经元号，$t$是当前层的神经元号。令线性组合${\sum }_j{w}_{jt}{z}_j=a_t$，则$z_t=h(a_t)$，$z_t$为激活值，$a_t$为线性组合值。

因此可以发现损失函数$L$对$w_{jt}$的依赖性全部都在$a_t$中，如下所示：

$$\frac{\partial L}{\partial w_{jt}}=\frac{\partial L}{\partial a_t}\frac{\partial a_t}{\partial w_{jt}}=\frac{\partial L}{\partial a_t}{z}_j$$

类比前面线性模型的例子，$z_j$就是上一层第$j$个输出即当前层的第$j$个输入。

然后定义

$$\frac{\partial L}{\partial a_t}={\delta }_t$$

${\delta }_t$可以理解为误差对神经元$t$的敏感程度，反向传播过程就是该敏感程度沿着网络反向传播的过程。

对于当前神经元$t$，我们已经分析了它的输入，接下去分析它的输出。

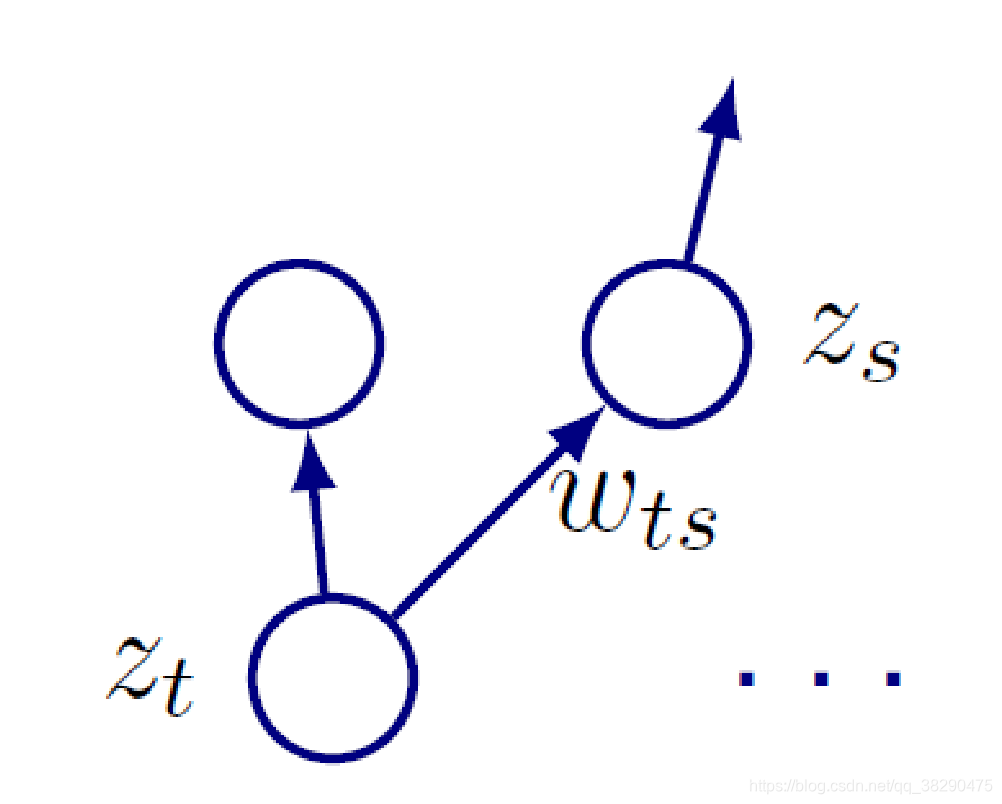
如图所示，神经元$t$会对其下一层的多个单元传递输入，令所有接收$t$输入的神经元所处的集合为$S$，可以得到下式：

$$a_s=\sum _{j:j\to s\in S}{w}_{js}h(a_j)$$

即，对于所属集合$S$的神经元$s$，其输入为上一层所有指向它的神经元输出之和。

因此当$j=t$时，$a_t$就和$a_s$发生关系，而$a_s$更加接近输出，因而对$L$的影响更靠前，如下式：

$$\begin{array}{rl}{\delta }_t& =\sum _{s\in S}\frac{\partial L}{\partial a_s}\frac{\partial a_s}{\partial a_t}\\ & =\sum _{s\in S}\frac{\partial L}{\partial a_s}{w}_{ts}{h}^{\prime }(a_t)\\ & =h^{\prime }(a_t)\sum _{s\in S}{w}_{ts}{\delta }_s\end{array}$$

到此，我们就将当前层的${\delta }_t$和下一层的${\delta }_s$联系在一起。

目前只是反向传播的过程，那在网络中反向传播具体是怎么表现的呢？又怎么和权值更新结合在一起呢？这两个问题将通过一个具体的例子进行解答。

2. 简单实例

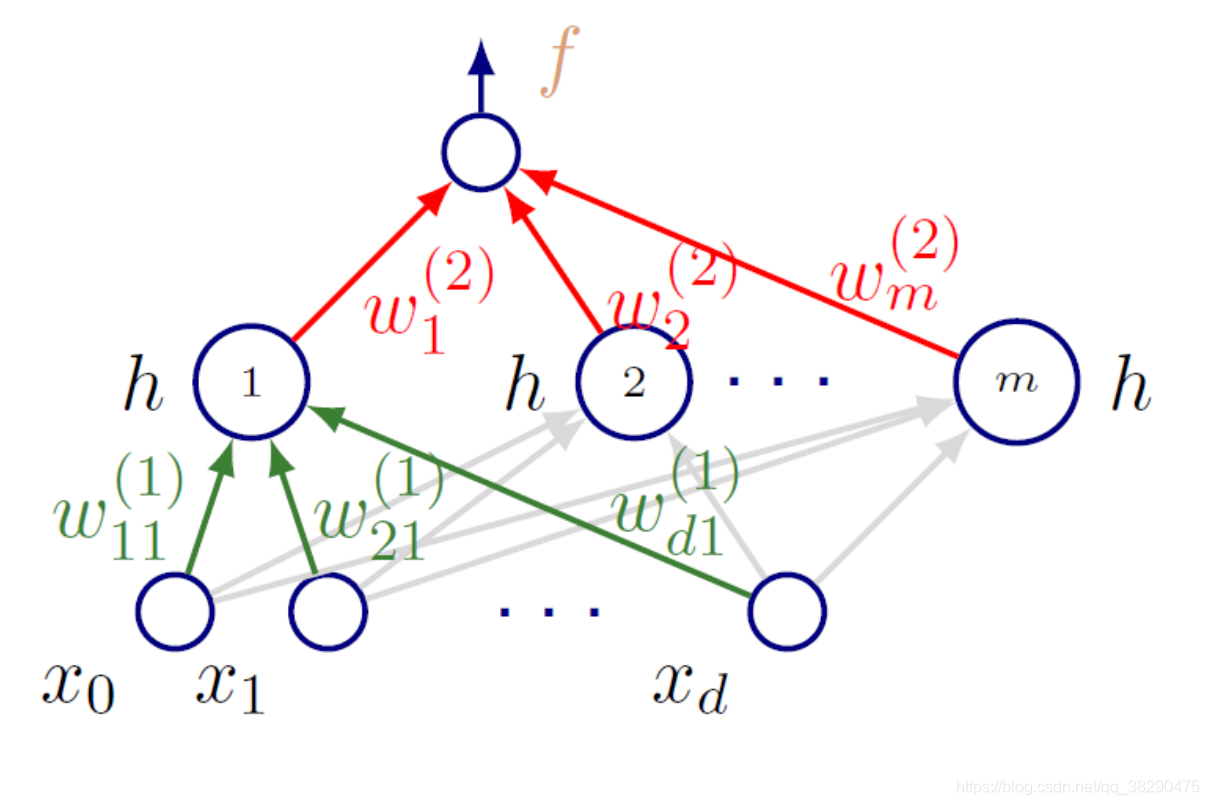
简单算例，网络结构如上图，并假设：

1. 输出：$\hat{y}=f(a)=a$
2. 隐层激活函数：$h(a)=\tanh (a)$，因此$h^{\prime }(a)=1-h(a{)}^2$

反向传播求解开始！

对于一个输入样本$x$，首先是前向传播过程：

1. 隐层输入：$a_j={\sum }_{i=0}^d{w}_{ij}^{(1)}{x}_i$
2. 隐层输出：$z_j=\tanh (a_j)$
3. 网络输出：$\hat{y}=a={\sum }_{j=0}^m{w}_j^{(2)}{z}_j$

因此对每一个样本的误差为：

$$L=\frac{1}{2}{\left(y-\hat{y}\right)}^2$$

对于输出单元，直接计算其$\delta$：

$$\delta =\frac{\partial L}{\partial a}=y-a=y-\hat{y}$$

然后计算隐层单元的$\delta$：

$${\delta }_j=h^{\prime }(a_j)w_j^{(2)}\delta =(1-z_j{)}^2{w}_j^{(2)}\delta$$

就是上面的传播公式，这里的集合$S$只有一个输出神经元。

下面就可以直接写出梯度：

$$\begin{array}{rl}& \frac{\partial L}{\partial w_{ij}^{(1)}}={\delta }_j{x}_i\\ & \frac{\partial L}{\partial w_j^{(2)}}=\delta z_j\end{array}$$

带入梯度下降法的权值更新公式：

$$\begin{array}{rl}& w_{ij}^{(1)}:=w_{ij}^{(1)}-\eta {\delta }_j{x}_i\\ & w_j^{(2)}:=w_j^{(2)}-\eta \delta z_j\end{array}$$

---

通过上面的例子，大家都能自己编程推导反向传播算法了嘛，哪里有疑问或者没说清楚的欢迎评论~~

下面就按照上述例子直观的编写反向传播算法。

3. python从零实现BP网络

【1】中有比较详细的DNN从零搭建过程，这里没有按照那么复杂的方式来些，纯粹是为了配合公式，使代码和公式更好理解。

首先准备数据集，人工生成一个回归任务的数据。

import numpy as np
import matplotlib.pyplot as plt

num_train, num_test = 100, 100
num_features = 10

true_w, true_b = np.ones((num_features, 1)) * 5, 2

features = np.random.normal(0, 1, (num_train + num_test, num_features))
noises = np.random.normal(0, 1, (num_train + num_test, 1)) * 0.0
labels = np.dot(features, true_w) + true_b + noises

x_train, x_test = features[:num_train, :], features[num_train:, :]
y_train, y_test = labels[:num_train], labels[num_train:]

再选择模型，进行训练。代码比较简单，结合注释以及第二节的公式阅读。基本和公式是一样的。

# 选择模型类型
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

def sigmoid_prime(x):
    return sigmoid(x) * (1 - sigmoid(x))


class Network(object):
    
    def __init__(self, sizes):
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y) for y in self.sizes[1:]]
        self.weights = [np.random.randn(x, y) / np.sqrt(x)
                        for (x, y) in zip(self.sizes[:-1], self.sizes[1:])]
        self.delta = []
        
    def feedforward(self, activation):
        # 公式前向传播
        a_hidden = np.dot(activation, self.weights[0]) + self.biases[0]
        z = sigmoid(a_hidden)
        a_out = np.dot(z, self.weights[1]) + self.biases[1]
        y_hat = a_out
        return y_hat
    
    def backpropagation(self, x, y):
        
        # -----------------------------前向传播开始-----------------------------------
        # 依次计算隐层输入，隐层输出，网络输出
        a_hidden = np.dot(x, self.weights[0]) + self.biases[0]
        z = sigmoid(a_hidden)
        a_out = np.dot(z, self.weights[1]) + self.biases[1]
        y_hat = a_out
        assert y_hat.all() == self.feedforward(x).all()
        # -----------------------------前向传播完成-----------------------------------
        
        # -----------------------------反向传播开始-----------------------------------
        # 依次计算误差，输出单元delta和隐层delta
        L = (y_hat - y) ** 2 / 2
        delta_output = (y_hat - y)
        delta_hidden = sigmoid_prime(a_hidden).reshape((-1,1)) * (self.weights[1] * delta_output)
        # -----------------------------反向传播结束-----------------------------------
        
        # -----------------------------权重更新开始-----------------------------------
        # 更新输入-隐层的权重
        delta1 = np.zeros_like(self.weights[0])
        for j in range(self.weights[0].shape[1]):
            for i in range(self.weights[0].shape[0]):
                delta1[i, j] = delta_hidden[j] * x[i]
#                 print(delta1[i, j])
                self.weights[0][i, j] -= 1 * delta1[i, j]
            self.biases[0][j] -= 1 * delta_hidden[j]
        # 更新隐层-输出的权重
        delta2 = np.zeros_like(self.weights[1])
        for j in range(self.weights[1].shape[1]):
            for i in range(self.weights[1].shape[0]):
                delta2[i, j] = delta_output[j] * z[i]
                self.weights[1][i, j] -= 0.001 * delta2[i, j]
            self.biases[1][j] -= 0.001 * delta_output[j]
    
def myloss(y_hat, y):
    return (y_hat - y) ** 2
    
net = Network([10, 20, 1])

all_loss = []
for epoch in range(100):
    loss = 0
    for isample in range(x_train.shape[0]):
        loss += myloss(net.feedforward(x_train[isample]), y_train[isample])
    all_loss.append(loss)
    for isample in range(x_train.shape[0]):
        net.backpropagation(x_train[isample], y_train[isample])

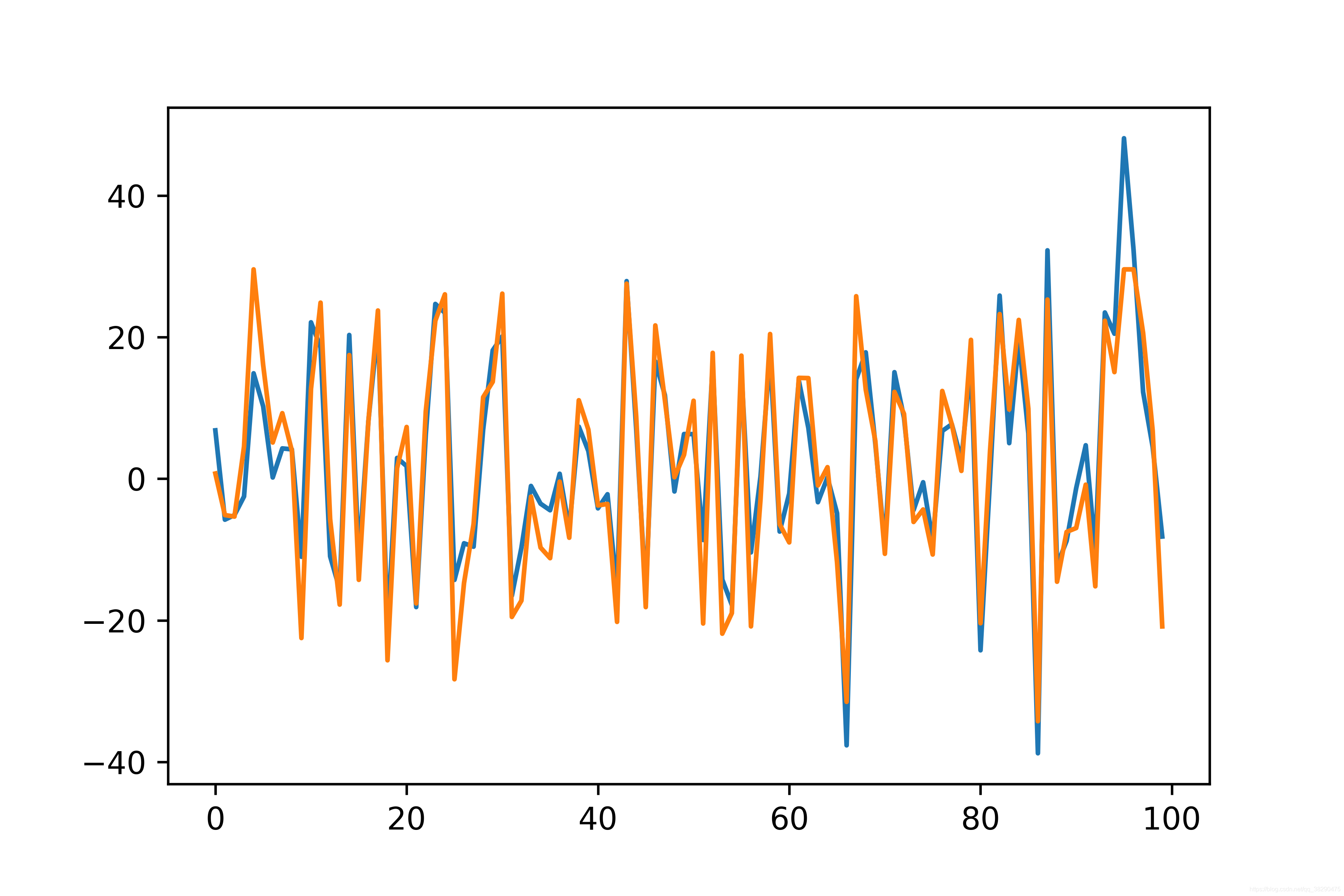
plt.plot(range(100), all_loss)

观察一下测试结果，基本拟合在一起了。表明上述推导以及比较低级的代码是有效的。

4. 总结BP算法公式

各资料的推导过程大同小异，很多都只有符号上的区别。

本文仅针对单个神经元进行推导，最终得到的几个公式如下，$a$为线性组合，$z$为激活值。

1. $\delta$法则：其中$t$为当前层的某个神经元，$s$为下一层的某个神经元。

$${\delta }_t=h^{\prime }(a_t)\sum _{s\in S}{w}_{ts}{\delta }_s$$

2. 权重更新：其中$t$为当前层的某个神经元，$j$为输入层的某个神经元。

$$\frac{\partial L}{\partial w_{jt}}=\frac{\partial L}{\partial a_t}\frac{\partial a_t}{\partial w_{jt}}=\frac{\partial L}{\partial a_t}{z}_j={\delta }_t{z}_j$$

后来发现这样的推导和《模式分类》【2】中的推导基本相同。

邱锡鹏老师的《神经网络与深度学习》【3】中对某层的神经元进行推导，最终得到的公式如下，$a$为激活值。

1. $\delta$法则：

$${\delta }^{(l)}=f_l^{{}^{\prime }}(z^{(l)})\circ (\left(w^{(l+1)}{)}^T{\delta }^{(l+1)}\right)$$

2. 权重更新：

$$\frac{\partial L}{\partial W^l}={\delta }^{(l)}{\left(a^{(l-1)}\right)}^T$$

统一符号，并矩阵化以后，两者是完全相同的。