matlab中最短路编程求解

大二的时候发在matlab中文论坛的，写过来方便看，也算记录一下了

以下为原文-----------------------------------------------------------------------------------------------

运筹学学完最短路问题心血来潮，想通过matalb编程实现一下。

算法步骤是课上学的，如下：
1.令起点标号为0，即b(s)=0,
2.找出所有已标号vi和未标号vj的弧的集合，B={(i,j)},如果这样的弧不存在或者终点vt已标号，则计算结束
3.计算集合B中弧k(i,j)=b(i)+d(i,j)的标号
4.选一个点标号，b(l)=min{k(i,j)|(i,j)属于B},在最小的k(i,j)的终点j处标号b(l),返回第二步。

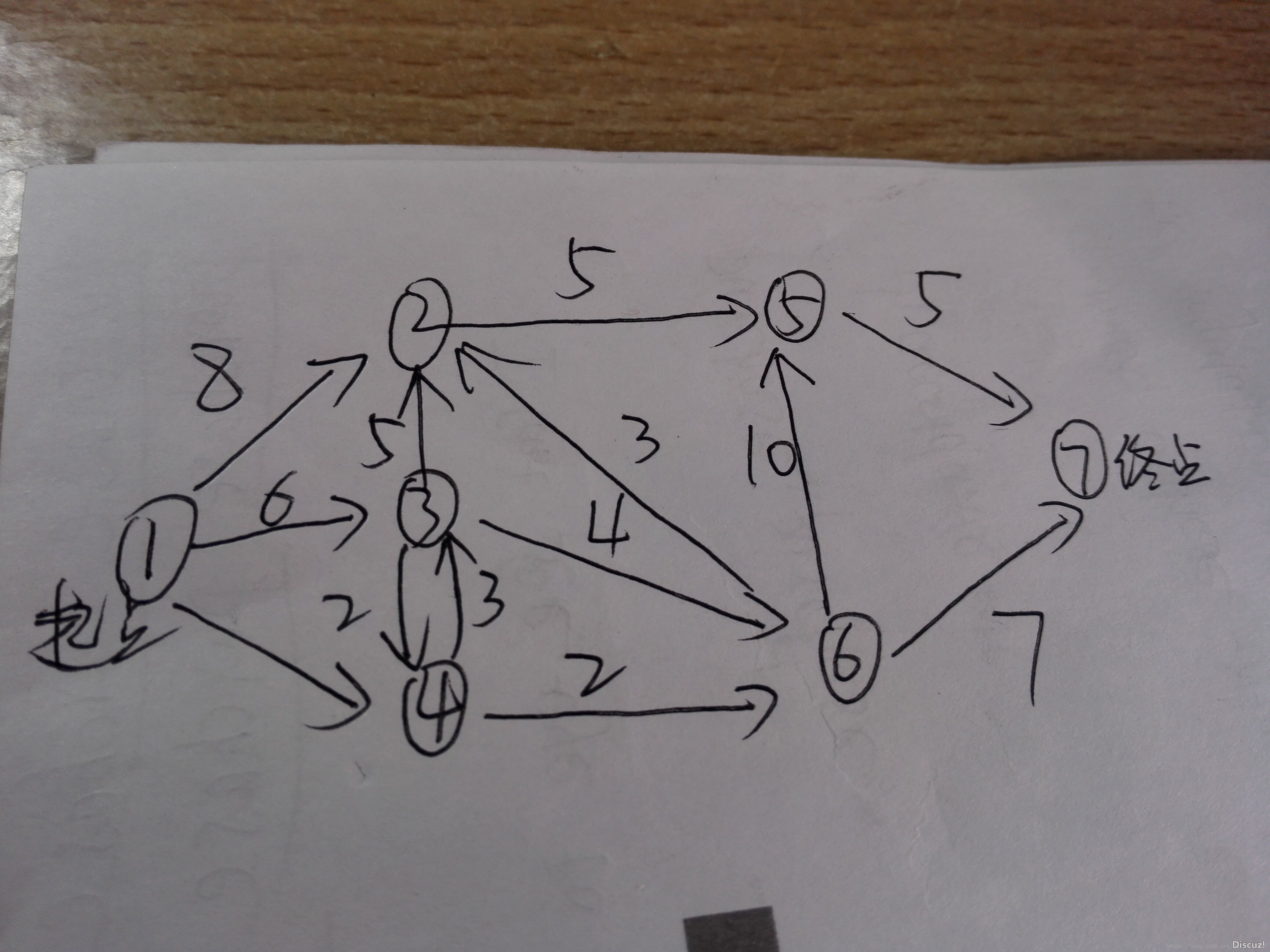
例题如图：

数字代表最短路问题里的运费或者时间。
废话不多bb,纯手工代码如下hhhh:
function [R,T] = minways( )
%最短路问题
D=[inf,8,6,2,inf,inf,inf;inf,inf,inf,inf,5,inf,inf;inf,5,inf,2,inf,4,inf;
    inf,inf,3,inf,inf,2,inf;inf,inf,inf,inf,inf,inf,5;
    inf,3,inf,inf,10,inf,7;inf,inf,inf,inf,inf,inf,inf];
R=[0,inf,inf,inf,inf,inf,inf];
Total=[1,2,3,4,5,6,7];
Done=[1];
Candidate=[2,3,4,5,6,7];
R(1)=0;
while (R(7)>1000)
a=length(Done);
b=length(Candidate);
t=1;
K={};
for i=1:a
    for j=1:b
  K{t}(i,j)=R(Done(i))+D(Done(i),Candidate(j));
    end
end
if a==1
[biaohao,number]=min(K{t});
else
x0=min(K{t});
[biaohao,number]=min(x0);
end
beibiaohao=Candidate(number);
Done=[Done,beibiaohao];
Candidate(Candidate==beibiaohao)=[];
R(beibiaohao)=biaohao;
t=t+1;
end
T=R(7);
end

写出来了很开心！！！
也发现了matalb的矩阵是多么的调皮，不听爸爸的话！

希望能给对这个问题感兴趣的提供一点微小的帮助。

END------------------------------------------------------------------------------------------------------------------------------------------------------

大二的时候好幼稚哈哈哈哈哈哈