注:笔者可能没有那么多时间写证明,如需自行查找吧(抱歉)
要系统学的看神仙yyc的blog
斐波那契数列
定 义 F [ 0 ] = 0 , F [ 1 ] = 1 , F [ n ] = F [ n − 1 ] + F [ n − 2 ] ( n > 1 ) \large 定义F[0]=0,F[1]=1,F[n]=F[n-1]+F[n-2](n>1) 定义F[0]=0,F[1]=1,F[n]=F[n−1]+F[n−2](n>1)
相关结论
-
F [ 1 ] + F [ 2 ] + . . . + F [ n ] = F [ n + 2 ] − 1 \large F[1]+F[2]+...+F[n]=F[n+2]-1 F[1]+F[2]+...+F[n]=F[n+2]−1
-
F [ 1 ] + F [ 3 ] + F [ 5 ] + . . . + F [ 2 n − 1 ] = F [ 2 n ] \large F[1]+F[3]+F[5]+...+F[2n-1]=F[2n] F[1]+F[3]+F[5]+...+F[2n−1]=F[2n]
证明: F [ 1 ] = F [ 2 ] , F [ 3 ] = F [ 4 ] − F [ 2 ] , F [ 5 ] = F [ 6 ] − F [ 4 ] F[1]=F[2],F[3]=F[4]-F[2],F[5]=F[6]-F[4] F[1]=F[2],F[3]=F[4]−F[2],F[5]=F[6]−F[4]累加即可 -
F [ 1 ] 2 + F [ 2 ] 2 + . . . + F [ n ] 2 = F [ n ] F [ n − 1 ] \large F[1]^2+F[2]^2+...+F[n]^2=F[n]F[n-1] F[1]2+F[2]2+...+F[n]2=F[n]F[n−1]
证明: F [ 2 ] 2 = F [ 2 ] ( F [ 3 ] − F [ 1 ] ) = F [ 2 ] F [ 3 ] − F [ 1 ] [ 2 ] F[2]^2=F[2](F[3]-F[1])=F[2]F[3]-F[1][2] F[2]2=F[2](F[3]−F[1])=F[2]F[3]−F[1][2]累加即可

生成函数(母函数)
定义
对
于
序
列
a
0
,
a
1
,
a
2
,
.
.
.
.
构
造
一
函
数
G
(
x
)
=
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
.
,
则
称
G
(
x
)
是
a
0
,
a
1
,
.
.
.
的
母
函
数
(
生
成
函
数
)
对于序列a_0,a_1,a_2,....构造一函数G(x)=a_0+a_1x+a_2x^2+....,则称G(x)是a_0,a_1,...的母函数(生成函数)
对于序列a0,a1,a2,....构造一函数G(x)=a0+a1x+a2x2+....,则称G(x)是a0,a1,...的母函数(生成函数)
主要思想
把离散数列和幂级数一一对应起来,
把离散数列间的相互结合关系对应成为幂级数间的运算关系,
最后由幂级数形式来确定离散数列的构造.
一般生成函数(OGF):
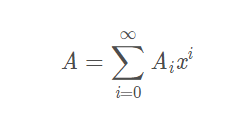
主要封闭形式
借yyc几张图

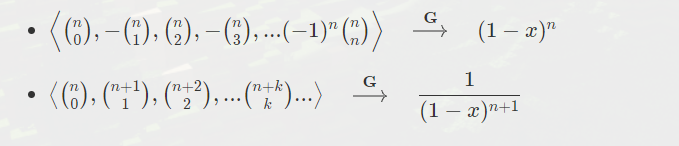
指数生成函数(EGF):
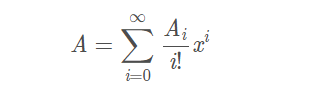
概率生成函数(PGF)
Ferrers图像
定义
上层格子数不少于下层格子数的图像称为Ferrers图像

基本性质
- 每行至少一个格子
- 绕虚线对称的图像仍然是Ferrers图像,这两个图像称为一对共轭Ferrers图像
基本结论
- 整数n拆分成k个数的和的拆分数,和数n拆分成最大数为k的拆分数相等。
证明:可以把n个格子用一个k行的Ferrers图像表示,根据第二条性质可以得出结论
线性常系数齐次递推关系(二阶)
二阶线性常系数齐次递推关系:
f [ n ] + a f [ n − 1 ] + b f [ n − 2 ] = 0 \large f[n]+af[n-1]+bf[n-2]=0 f[n]+af[n−1]+bf[n−2]=0
令
G
(
x
)
=
f
[
0
]
+
f
[
1
]
x
+
f
[
2
]
x
2
+
.
.
.
.
\ \ G(x)=f[0]+f[1]x+f[2]x^2+....
G(x)=f[0]+f[1]x+f[2]x2+....
则
a
x
G
(
x
)
=
a
f
[
0
]
x
+
a
f
[
1
]
x
2
+
f
[
2
]
x
3
+
.
.
.
.
axG(x)=\ \ \ \ \ af[0]x+af[1]x^2+f[2]x^3+....
axG(x)= af[0]x+af[1]x2+f[2]x3+....
b
x
2
G
(
x
)
=
b
f
[
0
]
x
2
+
a
f
[
1
]
x
3
+
f
[
2
]
x
4
+
.
.
.
.
\ \ \ \ bx^2G(x)=\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ bf[0]x^2+af[1]x^3+f[2]x^4+....
bx2G(x)= bf[0]x2+af[1]x3+f[2]x4+....
用自己定义自己,拿第一条式子加上两条可得
(
1
+
a
x
+
b
x
2
)
G
(
x
)
=
f
[
0
]
+
(
a
f
[
0
]
+
f
[
1
]
)
x
+
(
a
f
[
0
]
+
b
f
[
1
]
+
f
[
2
]
)
x
2
+
.
.
.
.
\ \ (1+ax+bx^2)G(x)=f[0]+(af[0]+f[1])x+(af[0]+bf[1]+f[2])x^2+....
(1+ax+bx2)G(x)=f[0]+(af[0]+f[1])x+(af[0]+bf[1]+f[2])x2+....
注意到 f [ n ] + a f [ n − 1 ] + b f [ n − 2 ] = 0 f[n]+af[n-1]+bf[n-2]=0 f[n]+af[n−1]+bf[n−2]=0 所以 [ x 2 ] [x^2] [x2]及后面的被消掉了
可得
(
1
+
a
x
+
b
x
2
)
G
(
x
)
=
f
[
0
]
+
(
a
f
[
0
]
+
f
[
1
]
)
x
(1+ax+bx^2)G(x)=f[0]+(af[0]+f[1])x
(1+ax+bx2)G(x)=f[0]+(af[0]+f[1])x
G
(
x
)
=
f
[
0
]
+
(
a
f
[
0
]
+
f
[
1
]
)
x
(
1
+
a
x
+
b
x
2
)
G(x)=\frac{f[0]+(af[0]+f[1])x}{(1+ax+bx^2)}
G(x)=(1+ax+bx2)f[0]+(af[0]+f[1])x
下面那个分母
1
+
a
x
+
b
x
2
1+ax+bx^2
1+ax+bx2对应的特征方程为
x
2
+
a
x
+
b
=
0
\large x^2+ax+b=0
x2+ax+b=0
把它的根解出来为
r
1
,
r
2
r_1,r_2
r1,r2,称之为特征根
然后
1
+
a
x
+
b
x
2
=
(
1
−
r
1
x
)
(
1
−
r
2
x
)
1+ax+bx^2=(1-r_1x)(1-r_2x)
1+ax+bx2=(1−r1x)(1−r2x)
对于
r
1
!
=
r
2
r_1!=r_2
r1!=r2
G
(
x
)
可
以
表
示
成
G
(
x
)
=
A
1
−
r
1
+
B
1
−
r
2
G(x)可以表示成\large G(x)=\frac{A}{1-r_1}+\frac{B}{1-r_2}
G(x)可以表示成G(x)=1−r1A+1−r2B
根据生成函数可得
F
[
n
]
=
A
r
1
n
+
B
r
2
n
F[n]=Ar_1^n+Br_2^n
F[n]=Ar1n+Br2n
根据
F
[
0
]
,
F
[
1
]
F[0],F[1]
F[0],F[1]把
A
,
B
A,B
A,B解出来就行了





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








