BP神经网络 简单介绍

BP神经网络

BP神经网络是指误差逆传播算法训练的多层前馈网络。

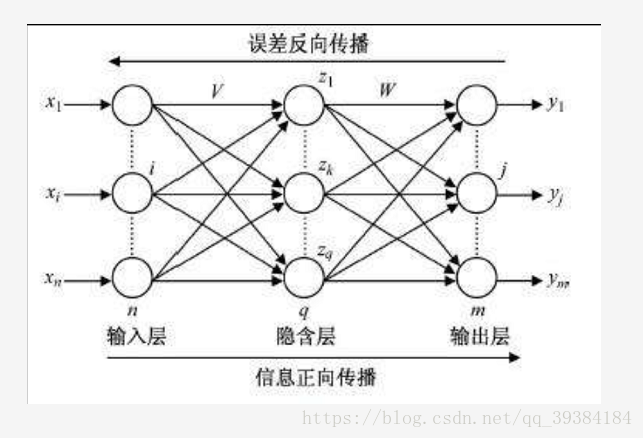
如下图为两层两层的BP神经网络（只有隐含层和输出层是参与计算和权值调整的节点层）。

• 图1：两层的BP神经网络

注：本文中用到的Python及其模块安装教程参见

---

结构和原理

在“单细胞”的神经网络里，实际上只有一层，即最后的输出层。在上图中有两层，第一层每个节点的输入都是一样的，都是$x_1，x_2，x_3\dots \dots x_n$。每个节点的超平面都可以用$g(v)=wv+b$来表示。但是，所有的节点最后输出的函数只有1或0两个状态，所以有激活函数为Logistic函数：

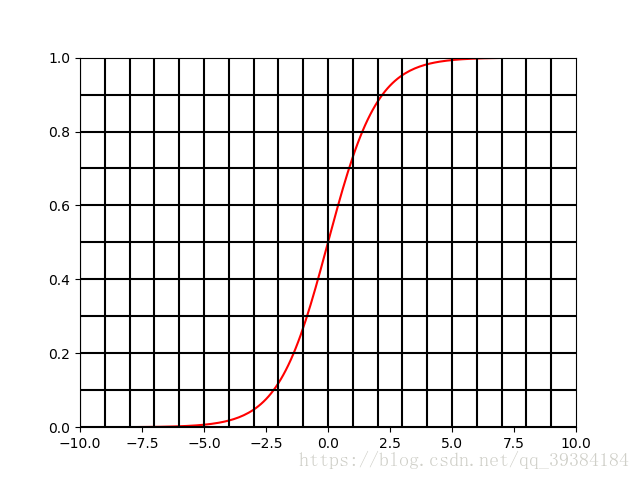
$f(v)=\frac{1}{1+e^{-(w^{T}v+b)}}$

$f(v)=\frac{1}{1+e^{-(w^{T}v+b)}}$这个函数其实是$f(t)=\frac{1}{1+e^{-t}}$和$t=w^{T}v+b$这两个函数组合变量代换形成的。$t=w^{T}v+b$在之前的人工神经网络中已经介绍过。$f(t)=\frac{1}{1+e^{-t}}$的图形如下图所示。

• 图2：$f(t)=\frac{1}{1+e^{-t}}$的图形

在t大于某个值时，函数值就是1，t小于某个值时，函数值就是0。

也可以写成以下的形式：

$f(t)=\frac{1}{1+e^{-mt}}$

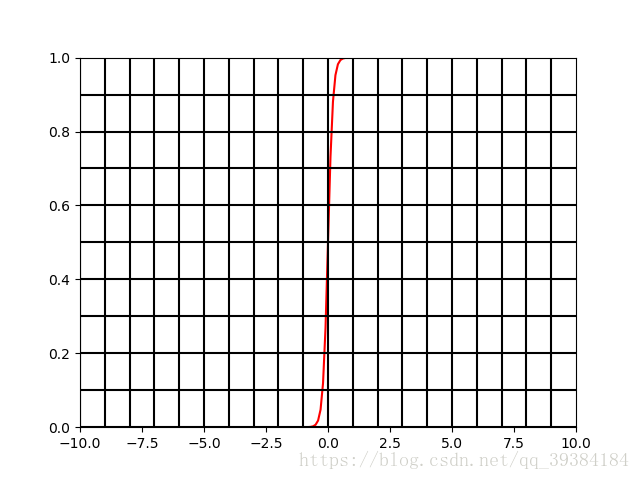
其中m是可以调整的参数，m越小曲线越平缓，m越大曲线越立陡，分类边界越明显。具体在每个应用中怎么取m的值要依情况而定，如果需要边界区分非常明显，那就把m的值设置地大一些。例如，m=10时，函数图形如下图。

• 图3：$f(t)=\frac{1}{1+e^{-10t}}$的图形

所以对于$f(v)=\frac{1}{1+e^{-(w^{T}v+b)}}$函数来说，函数会根据v的输入对应产生1和0两种函数值，而这里面待定的就是w这个矩阵，这就是在网络训练中需要决定的。而每个节点都有函数$f(v)=\frac{1}{1+e^{-(w^{T}v+b)}}$，而且每个节点之间都可能完全不一样。从上面的两层的BP神经网络的图可以看出，前面一层的输出结果作为后面一层节点的输入，最后一层的输出是n个不同的1或0，也就是说这个神经网络最多可以标识$2^n$种不同的分类。

---

训练过程

这里希望找到一种方法可以让设置好的各个权值能够匹配尽可能多的训练样本的分类情况，和线性回归中希望残差尽量小的思路一致。使用最小二乘法，最小二乘法的思路是，如果把误差表示成样本做自变量的函数，然后用求极值的方法来推导就可以找出这个误差最小情况下的各个系数值了。

• （一）误差计算。

隐含层节点的输入为：$h_i=w_{ih}{x}_i+b_h$。
隐含层节点的输出为：$h_o=f(h_i)$。
输出层节点的输入为：$y_i=w_{ho}+b_o$。
输出层节点的输出为：$y_o=f(y_i)$。

注意，这里面的$x_i，w_{ih}，w_{ho}，h_o，y_o$都是向量。

误差函数为：$E_i=d_{oi}-y_{oi}$

整个网络误差函数为：

$E=\frac{1}{2}{\sum }_{i=1}^n{E}_i=\frac{1}{2}{\sum }_{i=1}^n(d_{oi}-y_{oi}{)}^2$

这个函数前面的系数$\frac{1}{2}$只是为了之后求导方便，不影响函数的性质。

• （二）反向传播。

对这个误差函数进行求导求偏微分。

输出层误差偏微分：$\frac{\partial E}{\partial w_{ho}}=\frac{\partial E}{y_i}\frac{\partial y_i}{\partial w_{ho}}$

其中

$\frac{\partial E}{\partial y_i}=\frac{\partial \frac{1}{2}{\sum }_{i=1}^n(d_{oi}-y_{oi}{)}^2}{\frac{1}{2}{\sum }_{i=1}^n(d_{oi}-y_{oi}{)}^2{y}_i}$

$=-(d_{oi}-y_{oi})f^{‘}(y_i)=-{\delta }_o$

$\frac{\partial y_i}{\partial w_{ho}}=\frac{\partial (w_{ho}{h}_o+b_o)}{\partial w_{ho}}=h_o$

那么

$\frac{\partial E}{\partial w_{ho}}=\frac{\partial E}{y_i}\frac{\partial y_i}{\partial w_{ho}}=-{\delta }_o{h}_o$

误差的梯度

${\delta }_o=-(d_{oi}-y_{oi})f^{‘}(y_i)$

隐含层误差偏微分：$\frac{\partial E}{\partial w_{ih}}=\frac{\partial E}{\partial h_i}\frac{\partial h_i}{\partial w_{ih}}$

其中

$\frac{\partial E}{\partial h_i}=\frac{\partial \frac{1}{2}{\sum }_{i=1}^n(d_{oi}-y_{oi}{)}^2}{\partial h_o}\frac{\partial h_o}{\partial h_i}$

$=\frac{\partial \frac{1}{2}{\sum }_{i=1}^n(d_{oi}-f(y_i){)}^2}{\partial h_o}\frac{\partial h_o}{\partial h_i}$

$=\frac{\partial \frac{1}{2}{\sum }_{i=1}^n(d_{oi}-f(w_{ho}{h}_o+b_o){)}^2}{\partial h_0}\frac{\partial h_o}{\partial h_i}$

$=-(d_{oi}-y_{oi})f^{‘}(y_i)w_{ho}\frac{\partial h_o}{\partial h_i}$

$=-{\delta }_o{w}_{ho}{f}^{‘}(h_i)$

$=-{\delta }_h$

$\frac{\partial h_i}{\partial w_{ih}}=\frac{\partial (w_{ih}{x}_i+b_h)}{\partial w_{ih}}=x_i$

那么

$\frac{\partial E}{\partial w_{ih}}=-{\delta }_h{x}_i$

误差的梯度

${\delta }_h=({\delta }_o{w}_{ho})f^{‘}(h_i)$

（三）权值更新。

隐含层更新：

$w_{ih}^{N+1}=w_{ih}^N+\eta {\delta }_h{x}_i$

输出层更新：

$w_{ho}^{N+1}=w_{ho}^N+\eta {\delta }_o{h}_o$

---

过程解释

首先设置两套w作为两层网络各自的“超平面”的系数，然后输入一次完整的训练过程，就会有一个误差值出现。

接着就是一次一次地进行w的调整。调整的方法是，首先用最小二乘法的方式，找到一个误差和自变量的关系，然后求误差极值。

在最后的$w_{ih}^{N+1}=w_{ih}^N+\eta {\delta }_h{x}_i$和$w_{ho}^{N+1}=w_{ho}^N+\eta {\delta }_o{h}_o$这两个公式里，用的是试探性的方法。$+\eta {\delta }_h{x}_i$和$+\eta {\delta }_o{h}_o$是一种试探的“步长”，第一次分别设置了$w_{ih}$和$w_{ho}$，如果有误差，就试着往误差小的一边“走一步”，这就是一次一次迭代的目的。最后找到一个误差满足要求的点，把这一点的$w_{ih}$和$w_{ho}$都记录保存下来，网络就训练完毕了。这种步长试探的思路也叫梯度下降法。

---

想了解更多关于大数据和机器学习：大数据与机器学习专栏