34.在排序数组中查找元素的第一个和最后一个的位置

其实二分法真的挺复杂的，并不是像思想那么简单。。。。

看了一篇关于二分法的介绍，包括所有的细节，感觉受益良多

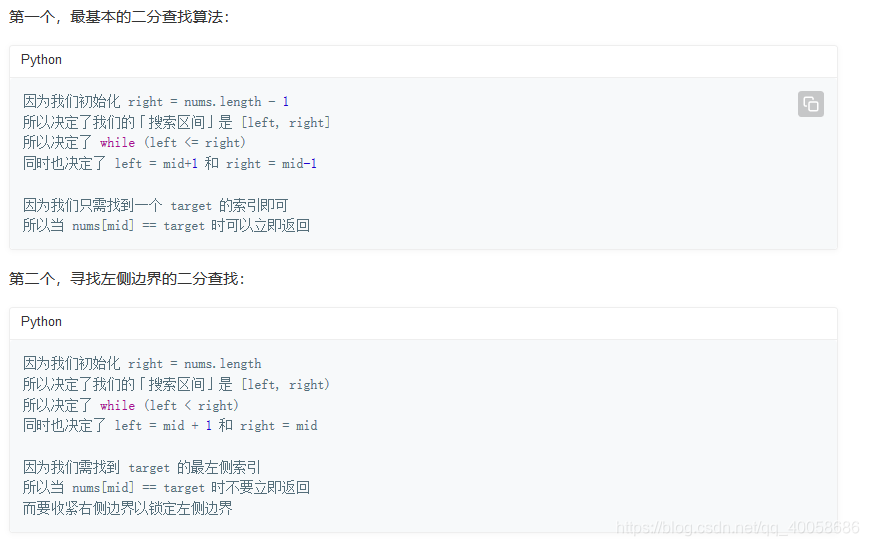
先来解决一下为什么有时候是max=len(num),有时候max=len(num)-1，和循环比较条件有时候是min<max，有时候是min<=max这个问题，这个问题解决了后面的就好办了，这其实是两组对应的。比如当你max=len(nums)-1时，你的循环条件就是min<=max，可以这样来思考。什么时候循环停止？循环结束时的状态是这样的：min=max+1,即[max+1,max]，这样的区间是不存在的，为空，这个时候就该返回-1（也就是没有得到结果）。而当你的max=len（nums）时，循环结束的情况是这样的[max,max]，而数组下标为max的话其实是越界的，那么我们就要在前一步停下来也就是max-1的时候就停下来。还有一个问题，为什么有时候max = mid，有时候max = mid+1的问题。

当我们判断了nums[mid]后，下一次考虑是不会再考虑这个mid的，而无论怎么样，我们都是min=mid+1，但是问题来了，右侧呢？其实是这样的，当你max = len(num)-1时，循环的最后一次是[min,max]这里的min等于max，这种情况下就相当于是左闭右开，即max的值不会越界，此时你要排除mid就必须是max = mid+1，而当你max=len(num）时，其实就是左闭右开，也就是右侧边界不会参与运算，此时就算你max=mid，虽然mid前面已经考虑过了，但是这里max本来就不会参与运算，所以也就不用max=mid+1了

 

其实总结下来就是这几点：

 

接下来就可以正式开始看这道题了。

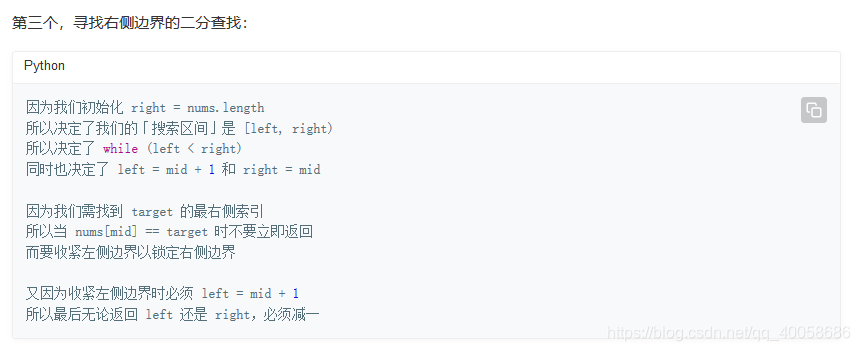
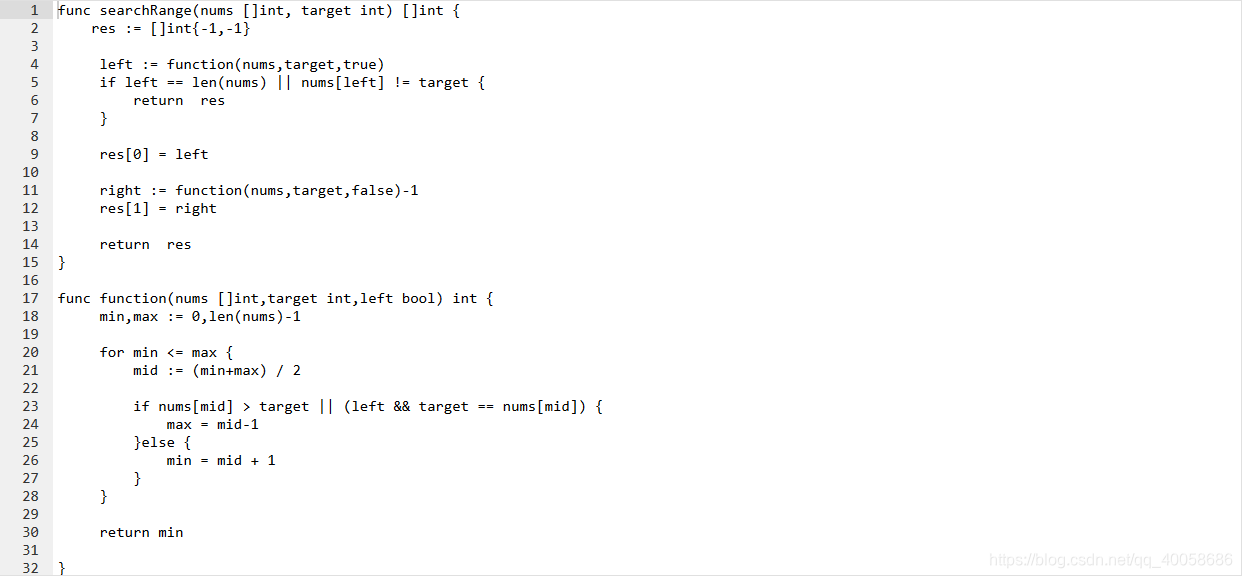
这道题是找出目标值在数组中出现的最初位置和最后出现的位置，我们同样可以用二分法，但是，稍微要有一点改变，也就是当你查询到该值时，不要停止，而是继续缩小范围，把你查到时的下标作为max，然后缩短，这样就能找到出现的最初位置了，而要搜索最后出现的位置就是这样的，当你查询到值等于目标值时，不要停止，而是缩小右侧范围，也就是min=mid+1，这里还有一个要注意的点是搜索最后出现的位置得到的值要进行减1操作，因为就算最后搜到了，他还是会进行min=mid+1，也就是现在的min并不是你想要的的结果，min-1才是。

大致思路如下，下面的就是代码：

 

 

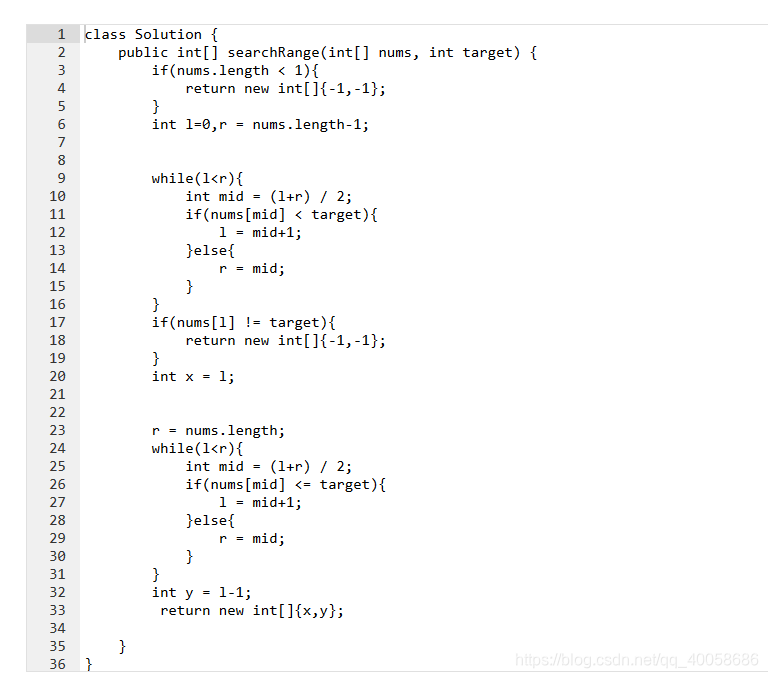
java版本：

   还是有一些细节会忘记，比如，这里当算右边的时候因为就算是最后一个元素和目标值相等，但是我还是向右边移动了一下，所以右边的最后结果需要对下标减1才是最右边的元素