2019牛客暑期多校训练营（第一场）

最新推荐文章于 2021-02-27 22:30:16 发布

兜率工

最新推荐文章于 2021-02-27 22:30:16 发布

阅读量224

点赞数

分类专栏：总结

本文链接：https://blog.csdn.net/qq_40679299/article/details/96714000

版权

总结专栏收录该内容

40 篇文章 2 订阅

订阅专栏

A 、Equivalent Prefixes 二分+笛卡尔树

B、 Integration 数学+找规律

C 、Euclidean Distance 贪心

E 、ABBA DP

F 、Random Point in Triangle 数学

H 、XOR 线性基

I 、Points Division 线段树+DP

J 、Fraction Comparision 大数

A 、Equivalent Prefixes

根据题意的描述，其实就是一颗笛卡尔树，所以直接二分比较两颗笛卡尔树是否相同即可。

#include<bits/stdc++.h>

using namespace std;

const int maxn=1e5+10;

int l[2][maxn],r[2][maxn];
int a[maxn],b[maxn];

bool judge(int n){
    stack<int>st;
    for(int i=1;i<=n;i++){          //建立a数组的笛卡尔树
        l[0][i]=r[0][i]=0;
        while(!st.empty()&&a[i]<a[st.top()]){
            l[0][i]=st.top();
            st.pop();
        }
        if(!st.empty()){
            r[0][st.top()]=i;
        }
        st.push(i);
    }
    while(!st.empty()) st.pop();
    for(int i=1;i<=n;i++){          //建立b数组的笛卡尔树
        l[1][i]=r[1][i]=0;
        while(!st.empty()&&b[i]<b[st.top()]){
            l[1][i]=st.top();
            st.pop();
        }
        if(!st.empty()){
            r[1][st.top()]=i;
        }
        st.push(i);
    }
    for(int i=1;i<=n;i++){          //比较两颗笛卡尔树是否相同
        if(l[0][i]!=l[1][i]||r[0][i]!=r[1][i]) return false;
    }
    return true;
}

int main(){

    int n;
    while(scanf("%d",&n)!=EOF){
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        for(int i=1;i<=n;i++){
            scanf("%d",&b[i]);
        }
        int L=0,R=n+1;
        while(L+1<R){
            int mid=L+R>>1;
            if(judge(mid)) L=mid;
            else R=mid;
        }
        printf("%d\n",L);
    }
    return 0;
}

B、 Integration

题意：

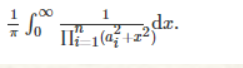并对1e9+7取模

分析：

找规律，计算出n=1，2，3，.........，n

可以发现答案为

参考博客：https://blog.csdn.net/ftx456789/article/details/96451366?tdsourcetag=s_pctim_aiomsg

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn=1e3+10;
const ll mod=1e9+7;

ll quick_pow(ll a,ll b,ll mod){
    ll ans=1;
    while(b){
        if(b&1) ans=(ans*a)%mod;
        b>>=1;
        a=(a*a)%mod;
    }
    return ans%mod;
}

ll inv(ll a,ll mod){
    return quick_pow(a,mod-2,mod);
}

ll a[maxn];

int main(){

    int n;
    while(scanf("%d",&n)!=EOF){
        for(int i=0;i<n;i++){
            scanf("%lld",&a[i]);
        }
        ll ans=0;
        for(int i=0;i<n;i++){
            ll res=1;
            for(int j=0;j<n;j++){
                if(i==j) continue;
                res=res*(a[j]*a[j]%mod-a[i]*a[i]%mod+mod)%mod;
            }
            res=res*2%mod*a[i]%mod;
            (ans+=inv(res,mod))%=mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

C 、Euclidean Distance

题意：

计算的最小值，

其中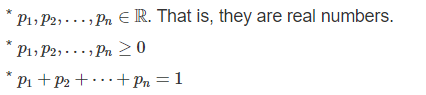

分析：

上式等价为 $(a_{i}-m*p_{i})^{2}$ 那么就相当于将m重新分配给a，那么将a排个序便可以贪心的计算最小值，每次不断减少当前最大的a，贪心的正确性也很好证明。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn=1e4+10;

ll a[maxn];

int main(){

    ll n,m;
    while(scanf("%lld%lld",&n,&m)!=EOF){
        for(int i=0;i<n;i++){
            scanf("%lld",&a[i]);
        }
        sort(a,a+n);
        int cnt=0;
        ll res=m;
        bool flag=false;
        for(int i=n-1;i>=1;i--){
            cnt++;
            ll tmp=a[i]-a[i-1];
            if(res>=cnt*tmp){
                res-=cnt*tmp;
            }else{
                res=cnt*a[i]-res;
                flag=true;
                break;
            }
        }
        if(!flag){
            cnt++;
            res=cnt*a[0]-res;
        }
        ll fm=cnt*cnt*m*m;
        ll fz=cnt*res*res;
        for(int i=n-cnt-1;i>=0;i--){
            fz+=cnt*cnt*a[i]*a[i];
        }
        ll gcd=__gcd(fm,fz);
        fm/=gcd;fz/=gcd;
        if(fm==1){
            printf("%lld\n",fz);
        }else{
            printf("%lld/%lld\n",fz,fm);
        }
    }
    return 0;
}

E 、ABBA

题意：

求有多少种长度为2*（n+m）的字符串使得可以凑出n个‘AB’ 和 m个’BA’，比如当n = 1， m = 1的时候，有ABAB，BAAB，BABA，ABBA四种满足的字符串，答案对1e9+7取模。

分析：

假设有一个合法串，因为子序列n个AB和m个BA，那么显然有前n个A必为AB的A，前m个B必为BA的B。因为如果我前n个A中有一个是BA的A，那我是不是可以从更后面随便找一个A给这个B用，那么显然前n个A必为AB的A。

我们假设DP[i][j]为i个Aj个B，放A：

如果i < n那么可以直接放这个A，理由如上

如果i >= n，那么我们要确保这个A能给前面的B当BA用，那么当前BA需要的A是j个，已经给他了i - n个，故(i - n) < j，则还可以继续放。注意 i - n != m. 这样的话就不能再放了。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const ll mod=1e9+7;
const int maxn=2e3+10;

ll dp[maxn][maxn];

int main(){

    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        for(int i=0;i<=n+m;i++){
            for(int j=0;j<=n+m;j++){
                dp[i][j]=0;
            }
        }
        dp[0][0]=1;
        for(int i=0;i<=n+m;i++){
            for(int j=0;j<=n+m;j++){
                if(i<n||(i>=n&&j>i-n&&i-n!=m)) dp[i+1][j]=(dp[i+1][j]+dp[i][j])%mod;
                if(j<m||(j>=m&&i>j-m&&j-m!=n)) dp[i][j+1]=(dp[i][j+1]+dp[i][j])%mod;
            }
        }
        printf("%lld\n",dp[n+m][n+m]);
    }
    return 0;
}

F 、Random Point in Triangle

这位博主解释的很清楚https://blog.csdn.net/ftx456789/article/details/96478804

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

int main(){

    ll x1,x2,x3,y1,y2,y3;
    while(scanf("%lld%lld%lld%lld%lld%lld",&x1,&y1,&x2,&y2,&x3,&y3)!=EOF){
        ll s=abs((x1*y2-x2*y1)+(x2*y3-x3*y2)+(x3*y1-x1*y3))*11ll;
        printf("%lld\n",s);
    }
    return 0;
}

H 、XOR

题意：

给出一个序列，计算子序列异或和是0的所有子序列大小的和。

分析：

看了题解说的是线性基，然后补了下这东西，感觉补提学新知识就是爽呀。

原题可以转化为计算每个数在集合中出现的次数，同时根据线性基的性质，线性基里面的数的个数唯一，并且在保持性质一的前提下，数的个数是最少的，那么可以构造一个线性基，设其中基数个数是r，那么其余n-r个数就都能用这r个数表示出来，那么对于线性基外的一个数x来说，他与其他n-r-1个数组成的集合均能在线性基中找到一组数使得异或和为0，那么线性基外的每个数的贡献即为 $(n-r)\times2^{n-r-1}$ ，对于线性基内的每个数，如果用其余n-1个数字能够表示，那么说明存在另外一个线性基能够表示所有的n个数字，而且这个线性基数字个数也是r，因此这个点的贡献还是 $2^{n-r-1}$ ，如果用其余n-1个数字不能表示，那么说明只要选了这个数字就不存在一种方案使得最后异或和为0，因此贡献为0.

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

struct Linear_Basis{

    ll d[64],cnt;
    Linear_Basis(){
        memset(d,0,sizeof d);
        cnt=0;
    }
    bool insert(ll val){
        for(int i=63;i>=0;i--){
            if(val&(1ll<<i)){
                if(!d[i]){
                    d[i]=val;
                    cnt++;
                    break;
                }
                val^=d[i];
            }
        }
        return val>0;
    }
};

const int maxn=1e5+10;
const ll mod=1e9+7;

ll a[maxn];
bool vis[maxn];
ll Pow[maxn];

void init(){
    Pow[0]=1ll;
    for(int i=1;i<maxn;i++){
        Pow[i]=Pow[i-1]*2ll%mod;
    }
}

int main(){

    init();
    int n;
    while(scanf("%d",&n)!=EOF){
        Linear_Basis lb1,lb2,lb3;
        vector<ll> v;
        for(int i=0;i<n;i++){
            scanf("%lld",&a[i]);
            vis[i]=0;
            if(lb1.insert(a[i])){
                v.push_back(a[i]);
                vis[i]=1;
            }
        }
        if(lb1.cnt==n){
            printf("0\n");
            continue;
        }
        ll ans=0;
        ans=(ll)(n-lb1.cnt)*Pow[n-lb1.cnt-1]%mod;
        for(int i=0;i<n;i++){
            if(!vis[i]){
                lb2.insert(a[i]);
            }
        }
        for(int i=0;i<lb1.cnt;i++){
            lb3=lb2;
            for(int j=0;j<lb1.cnt;j++){
                if(i==j) continue;
                lb3.insert(v[j]);
            }
            if(!lb3.insert(v[i])){
                ans=(ans+Pow[n-lb1.cnt-1])%mod;
            }
        }
        printf("%lld\n",ans);
    }
    return 0;
}

I 、Points Division

题意：

给你n个点，第i个点在的位置为(xi,yi)，有两个属性值(ai,bi)。现在让你把这n个点划分为A和B两个部分，使得最后不存在i∈A和j∈B，使得xi>=xj且yi<=yj。然后对于所有的划分方法，找到并输出

$\large max(\sum_{i\in A}a_i+\sum_{j\in B}b_j)$

分析：

首先那个划分的限制条件看起来复杂，其实就是A中不存在点在B中任意一个点的右下角。根据这个限制，显然对于任意合法的划分，我都可以找到一条不下降的折线把所有点划分为两个部分。左上部分为A，右下部分为B。我们不妨移动这个折线，使得B中的部分点在边界上。如下图，是一种合法的方案。

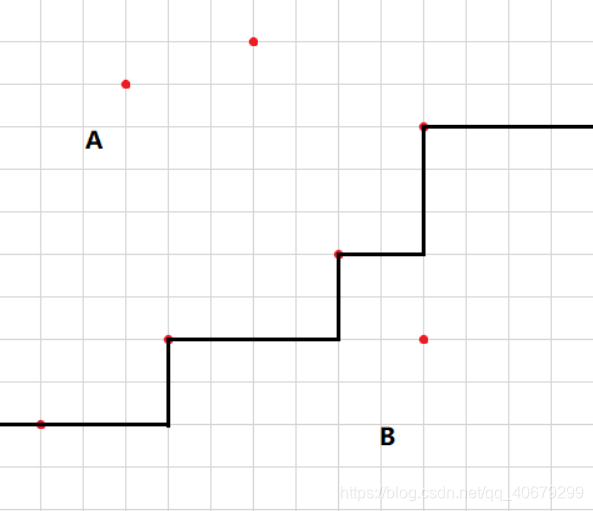
现在要求的是两部分和的最大值，我们考虑DP。设dp[i]表示到目前为止，第i个点在折线上时的和的最大值。然后考虑每增加一个点会产生什么贡献。显然，增加一个点i之后，对于之前考虑过的比他高的点，他应该在B中，他的贡献是bi；相反，对于那些比他低的点，他应该在A中，他的贡献就是ai。于是，我们可以动态维护dp的数值，对于一个新加入的点i有：
$\large dp[j]=\begin{cases}dp[j]+b_i &j<i,y_j>y_i\\dp[j]+a_i &j<i,y_j<y_i\end{cases}$

另外，对于当前点i，此时当他在折线上时的最大值为：

$\large dp[i]=b_i+\max \limits_{1\le j<i,y_j<y_i}dp[j]$

具体到这道题，由于增加一个点产生的贡献其实是对区间的影响，然后转移的时候也需要求区间的最大值，所以我们可以把y坐标离散化并建立一棵线段树，维护区间最大值。需要注意的是，我们需要虚拟一个高度为0的点作为第一个点的参照。注意的两个点就是建立一个虚拟节点，因为DP要设立初始值。还有对y的排序是从大到小，因为不可能这个点下面的点（x相同）空几个再在上面取。

#include<bits/stdc++.h>

using namespace std;

typedef long long ll;

const int maxn=1e5+10;
const ll inf=0x3f3f3f3f3f3f3f3f;

struct node{
    ll x,y,a,b;
    bool operator < (node p){
        if(x==p.x) return y>p.y;
        return x<p.x;
    }
}p[maxn];

int n,m,num[maxn],tot;

struct Segment_Tree{

    #define ls (i<<1)
    #define rs (i<<1|1)

    struct node{
        ll mx,lazy;
        int l,r;
    }tree[maxn<<2];

    inline void push_up(int i){
        tree[i].mx=max(tree[ls].mx,tree[rs].mx);
    }

    void build(int i,int l,int r){
        tree[i]=node{0,0,l,r};
        if(l==r){
            tree[i].mx=-inf;
            tree[i].lazy=0ll;
            return ;
        }
        int mid=l+r>>1;
        build(ls,l,mid);
        build(rs,mid+1,r);
        push_up(i);
    }

    inline void push_down(int i){
        tree[ls].lazy+=tree[i].lazy;
        tree[rs].lazy+=tree[i].lazy;
        tree[ls].mx+=tree[i].lazy;
        tree[rs].mx+=tree[i].lazy;
        tree[i].lazy=0;
    }

    void add_update(int i,int l,int r,ll x){
        if(l>r) return ;
        if(tree[i].l==l&&tree[i].r==r){
            tree[i].lazy+=x;
            tree[i].mx+=x;
            return ;
        }
        if(tree[i].lazy!=0) push_down(i);
        int mid=tree[i].l+tree[i].r>>1;
        if(mid>=r) add_update(ls,l,r,x);
        else if(mid<l) add_update(rs,l,r,x);
        else{
            add_update(ls,l,mid,x);
            add_update(rs,mid+1,r,x);
        }
        push_up(i);
    }

    void change_update(int i,int pos,ll x){
        if(tree[i].l==tree[i].r){
            tree[i].mx=max(tree[i].mx,x);
            return ;
        }
        if(tree[i].lazy!=0) push_down(i);
        int mid=tree[i].l+tree[i].r>>1;
        if(mid>=pos) change_update(ls,pos,x);
        else change_update(rs,pos,x);
        push_up(i);
    }

    ll query_max(int i,int l,int r){
        if(l>r) return 0;
        if(tree[i].l==l&&tree[i].r==r){
            return tree[i].mx;
        }
        if(tree[i].lazy!=0) push_down(i);
        int mid=tree[i].l+tree[i].r>>1;
        if(mid>=r) return query_max(ls,l,r);
        else if(mid<l) return query_max(rs,l,r);
        else return max(query_max(ls,l,mid),query_max(rs,mid+1,r));
    }

}seg;

int main(){

    while(scanf("%d",&n)!=EOF){
        tot=0;
        for(int i=1;i<=n;i++){
            scanf("%lld%lld%lld%lld",&p[i].x,&p[i].y,&p[i].a,&p[i].b);
            num[++tot]=p[i].y;
        }
        sort(num+1,num+1+tot);
        tot=unique(num+1,num+1+tot)-num-1;
        for(int i=1;i<=n;i++){
            p[i].y=lower_bound(num+1,num+1+tot,p[i].y)-num+1;
        }
        tot++;
        sort(p+1,p+1+n);
        seg.build(1,1,tot);
        seg.change_update(1,1,0);
        for(int i=1;i<=n;i++){
            ll cur=seg.query_max(1,1,p[i].y);
            seg.change_update(1,p[i].y,cur+p[i].b);
            seg.add_update(1,p[i].y+1,tot,p[i].b);
            seg.add_update(1,1,p[i].y-1,p[i].a);
        }
        printf("%lld\n",seg.tree[1].mx);
    }
    return 0;
}

J 、Fraction Comparision

java的一道大数题，不过题解给的方法也很巧妙。

import java.math.BigInteger;
import java.util.Scanner;

public class Main{

	public static void main(String args[]) {
		Scanner in=new Scanner(System.in);
		while(in.hasNext()) {
			BigInteger x=in.nextBigInteger(),a=in.nextBigInteger(),y=in.nextBigInteger(),b=in.nextBigInteger();
			BigInteger p=x.multiply(b);
			BigInteger q=y.multiply(a);
			if(p.compareTo(q)==0) {
				System.out.println("=");
			}else if(p.compareTo(q)<0) {
				System.out.println("<");
			}else {
				System.out.println(">");
			}
		}
	}
}

兜率工

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
2019牛客暑期多校训练营（第一场）

目录A、Equivalent Prefixes 二分+笛卡尔树B、 Integration 数学+找规律C 、Euclidean Distance 贪心E 、ABBA DPF 、Random Point in Triangle 数学H 、XOR 线性基I 、Points Division 线段树+DPJ 、Fraction Comparis...
复制链接

扫一扫