「2019南昌网络赛H」The Nth Item【分块+斐波那契数列循环节+矩阵快速幂】

最新推荐文章于 2021-03-26 19:58:44 发布

原创最新推荐文章于 2021-03-26 19:58:44 发布 · 269 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#2019南昌网络赛H #矩阵快速幂 #分块 #斐波那契数列循环节

分块同时被 2 个专栏收录

6 篇文章

订阅专栏

矩阵快速幂

1 篇文章

订阅专栏

本文介绍了一种高效的解决斐波那契数列问题的方法，通过矩阵快速幂和循环节预处理技巧，避免了传统递归或迭代算法的时间复杂度过高的问题。适用于大规模数据集和高精度计算场景。

The Nth Item

题面

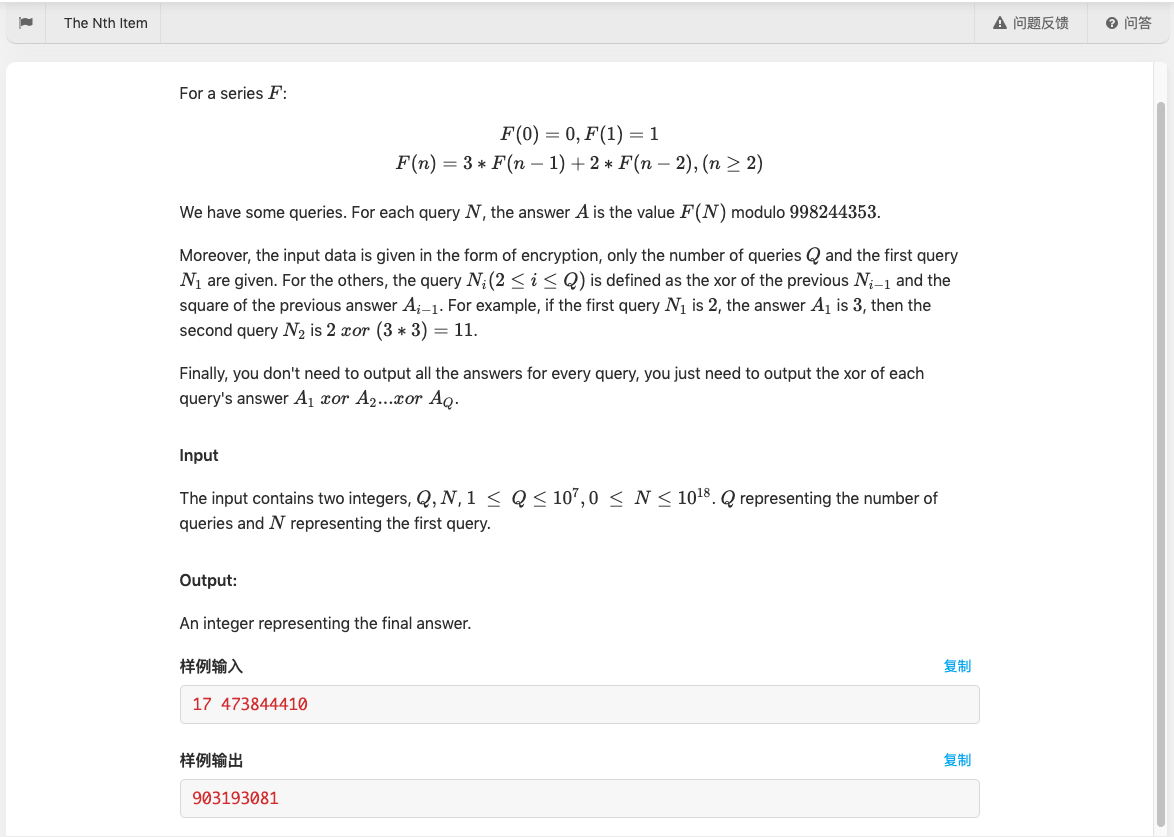
在这里插入图片描述

题意

就是求斐波那契数列的值， $10^7$ 个询问

题解

显然直接矩阵快速幂会 $T$ ，所以考虑找出循环节 $(499122176)$ ，然后将这个循环节分块并且预处理系数矩阵的 $[0, 块大小 - 1]$ 次方以及每块开始的那个位置的矩阵就行了

代码

#pragma GCC optimize(3)
#include<bits/stdc++.h>

using namespace std;
const int maxn=1e5+10;
const int maxm=3;
const long long mod=998244353;

struct matrix{
    long long mat[maxm][maxm];int siz;
    matrix(int a=maxm){
        siz=a-1;
        memset(mat,0,sizeof(mat));
    }
    matrix operator*(const matrix &b){
        matrix res;
        for(int i=1;i<=siz;i++){
            for(int k=1;k<=siz;k++){
                if(mat[i][k]){
                    for(int j=1;j<=siz;j++){
                        if(b.mat[k][j]){
                            res.mat[i][j]=(res.mat[i][j]+(mat[i][k]*b.mat[k][j]));
                            if(res.mat[i][j]>=mod) res.mat[i][j]%=mod;
                        }
                    }
                }
            }
        }
        return res;
    }
    matrix pow(long long k){
        matrix res,tmp=*this;
        for(int i=1;i<=siz;i++) res.mat[i][i]=1;
        while(k){
            if(k&1) res=res*tmp;
            tmp=tmp*tmp;
            k>>=1;
        }
        return res;
    }
    void print(){
        for(int i=1;i<=siz;i++){
            for(int j=1;j<=siz;j++){
                printf("%lld%c",mat[i][j],j==siz?'\n':' ');
            }
        }
    }
}a,b,res,fac[maxn],cifang[maxn];


void init()
{
    a.mat[1][1]=3;
    a.mat[1][2]=2;
    a.mat[2][1]=1;
    a.mat[2][2]=0;

    b.mat[1][1]=1;
    b.mat[1][2]=0;
    b.mat[2][1]=0;
    b.mat[2][2]=0;

    cifang[0].mat[1][1]=1;
    cifang[0].mat[2][2]=1;
}

int q;
long long n,ans,sta[maxn];
int main()
{
    init();
    res=a.pow(99999)*b;
    for(int i=100000,j=2;i<=5e8;i+=100000,j++){
        fac[j]=res;
        sta[j]=i;
        res=a.pow(100000)*res;
    }
    for(int i=1;i<=100000;i++) {
        cifang[i]=cifang[i-1]*a;
    }
    scanf("%d %lld",&q,&n);
    long long answe=0;
    for(int i=1;i<=q;i++) {
        int need=n%499122176;
        if(need<=1) {
            ans=need;
        }else{
            int belong=(need/100000)+1;
            int rest=need-1LL*(belong-1)*100000;
            if(belong==1) {
                res=cifang[need-1]*b;
                ans=res.mat[1][1];
            }else{
            
                res=cifang[need-sta[belong]]*fac[belong];
                ans=res.mat[1][1];
            }
        }
        answe^=ans;
        n=n^(ans*ans);
    }
    printf("%lld\n",answe);
}