146、【动态规划】leetcode ——746. 使用最小花费爬楼梯：递归法+迭代法（C++/Python版本）

题目描述

原题链接：746. 使用最小花费爬楼梯

解题思路

动态规划五部曲：

（1）dp[i]的含义： 跳到第i阶楼梯，需要的费用（注意：跳到第i阶的费用来源于i-1或i-2，与本层第i阶费用无关）
（2）递推公式： dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + csot [i - 2])，首先要明确的是当位于第i层时并需要使用第i层的花费，只有跳到第i + 1层或第i + 2层时，才花费第i层费用。因此，若想跳到第i层，则可能需要前i-1层的费用和跳到i - 1层所需要的费用，或者前i-2层。
（3）dp数组初始化： dp[0] = 0, dp[1] = 0, dp[2] = min(dp[0], dp[1])。题中条件是初始位置可以是0或者1，如果想要位于2，则可能的情况是从0或者从1跳过去。
（4）确定遍历顺序： 递归法从大到小，迭代法从小到大。
（5）举例推导dp数组：

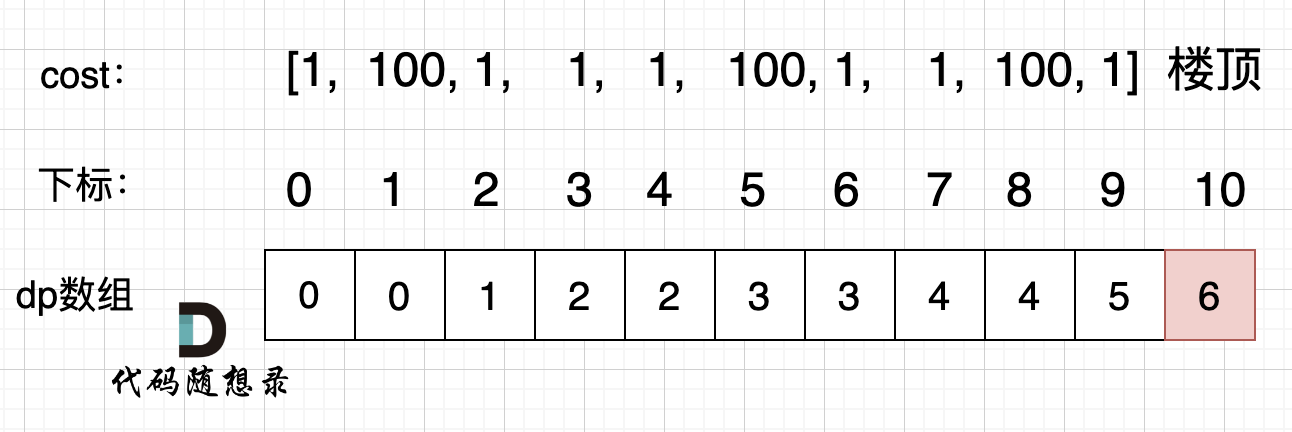
（1）递归法

class Solution {
public:
    int dp[1001];
    int minCostClimbingStairs(vector<int>& cost) {     
        if(cost.size() <= 1)            return 0;
        int n = cost.size();
        if(dp[n] != 0)                  return dp[n];
        vector<int> cost1(cost.begin(), cost.end() - 1);
        vector<int> cost2(cost.begin(), cost.end() - 2);
        dp[n] = min(minCostClimbingStairs(cost1) + cost[n - 1], minCostClimbingStairs(cost2) + cost[n - 2]);
        
        return dp[n];
    }
};

（2）迭代法

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {     
        if(cost.size() <= 1)            return 0;
        int dp[1001] = {0, 0, min(cost[0], cost[1])};
        for(int i = 3; i <= cost.size(); i++) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};

Python

n = int(input())
cost = list(map(int, input().split()))

if n <= 1:
    print(0)
else:
	dp = [0] * (n + 1)
	dp[0], dp[1], dp[2] = 0, 0, min(cost[0], cost[1])
	
	for i in range(3, n + 1):
	    dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
	
	print(dp[n])

变量优化
仅设置两个变量来记录，dp1始终指向最后一个数，dp0指向其前一个数。

class Solution {
public:
    int dp[1001];
    int minCostClimbingStairs(vector<int>& cost) {     
        if(cost.size() <= 1)            return 0;
        int sum = 0, dp0 = 0, dp1 = 0;        
        for(int i = 2; i <= cost.size(); i++) {
            sum = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
            dp0 = dp1;
            dp1 = sum;
        }
        return dp1;
    }
};

参考文章：746. 使用最小花费爬楼梯