看了大牛的线段树讲解,受益匪浅,无奈篇幅太长,自己总结了一下其中比较重要的要点:
摘自:http://blog.csdn.net/yitongjun/article/details/53193724
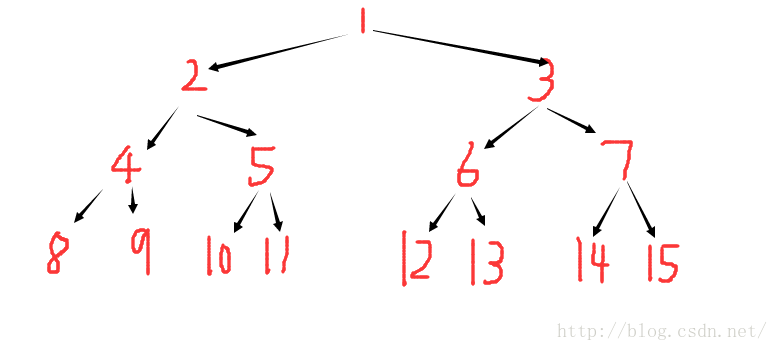
线段树的存储结构:
线段树是用数组来模拟树形结构,对于每一个节点R ,左子节点为 2*R (一般写作R<<1)右子节点为 2*R+1(一般写作R<<1|1)
然后以1为根节点,所以,整体的统计信息是存在节点1中的。
这么表示的原因看下图就很明白了,左子树的节点标号都是根节点的两倍,右子树的节点标号都是左子树+1:
线段树需要的数组元素个数是: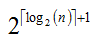 ,一般都开4倍空间,比如: int A[n<<2];
,一般都开4倍空间,比如: int A[n<<2];
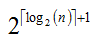 ,一般都开4倍空间,比如: int A[n<<2];
,一般都开4倍空间,比如: int A[n<<2];
递归实现线段树:
#define maxn 100007 //元素总个数
#define ls l,m,rt<<1
#define rs m+1,r,rt<<1|1
int Sum[maxn<<2],Add[maxn<<2];//Sum求和,Add为懒惰标记
int A[maxn],n;//存原数组数据下标[1,n]
建树
//PushUp函数更新节点信息 ,这里是求和
void PushUp(int rt){Sum[rt]=Sum[rt<<1]+Sum[rt<<1|1];}
//Build函数建树
void Build(int l,int r,int rt){ //l,r表示当前节点区间,rt表示当前节点编号
if(l==r) {//若到达叶节点
Sum[rt]=A[l];//储存数组值
return;
}
int m=(l+r)>>1;
//左右递归
Build(l,m,rt<<1);
Build(m+1,r,rt<<1|1);
//更新信息
PushUp(rt);
}
点修改
假设A[L]+=C:
void Update(int L,int C,int l,int r,int rt){//l,r表示当前节点区间,rt表示当前节点编号
if(l==r){//到叶节点,修改
Sum[rt]+=C;
return;
}
int m=(l+r)>>1;
//根据条件判断往左子树调用还是往右
if(L <= m) Update(L,C,l,m,rt<<1);
else Update(L,C,m+1,r,rt<<1|1);
PushUp(rt);//子节点更新了,所以本节点也需要更新信息
} 区间修改:
假设A[L,R]+=C
void Update(int L,int R,int C,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号
if(L <= l && r <= R){//如果本区间完全在操作区间[L,R]以内
Sum[rt]+=C*(r-l+1);//更新数字和,向上保持正确
Add[rt]+=C;//增加Add标记,表示本区间的Sum正确,子区间的Sum仍需要根据Add的值来调整
return ;
}
int m=(l+r)>>1;
PushDown(rt,m-l+1,r-m);//下推标记
//这里判断左右子树跟[L,R]有无交集,有交集才递归
if(L <= m) Update(L,R,C,l,m,rt<<1 if="" r=""> m) Update(L,R,C,m+1,r,rt<<1|1);
PushUp(rt);//更新本节点信息
}
区间查询:
询问A[L,R]的和
首先是下推标记的函数:
void PushDown(int rt,int ln,int rn){
//ln,rn为左子树,右子树的数字数量。
if(Add[rt]){
//下推标记
Add[rt<<1]+=Add[rt];
Add[rt<<1|1]+=Add[rt];
//修改子节点的Sum使之与对应的Add相对应
Sum[rt<<1]+=Add[rt]*ln;
Sum[rt<<1|1]+=Add[rt]*rn;
//清除本节点标记
Add[rt]=0;
}
}
然后是区间查询的函数:
int Query(int L,int R,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号
if(L <= l && r <= R){
//在区间内,直接返回
return Sum[rt];
}
int m=(l+r)>>1;
//下推标记,否则Sum可能不正确
PushDown(rt,m-l+1,r-m);
//累计答案
int ANS=0;
if(L <= m) ANS+=Query(L,R,l,m,rt<<1 if="" r=""> m) ANS+=Query(L,R,m+1,r,rt<<1|1);
return ANS;
}
函数调用
//建树
Build(1,n,1);
//点修改
Update(L,C,1,n,1);
//区间修改
Update(L,R,C,1,n,1);
//区间查询
int ANS=Query(L,R,1,n,1);
非递归实现线段树:
#define maxn 100007
int A[maxn],n,N;//原数组,n为原数组元素个数 ,N为扩充元素个数
int Sum[maxn<<2];//区间和
int Add[maxn<<2];//懒惰标记
建树
void Build(int n){
//计算N的值
N=1;while(N < n+2) N <<= 1;
//更新叶节点
for(int i=1;i<=n;++i) Sum[N+i]=A[i];//原数组下标+N=存储下标
//更新非叶节点
for(int i=N-1;i>0;--i){
//更新所有非叶节点的统计信息
Sum[i]=Sum[i<<1]+Sum[i<<1|1];
//清空所有非叶节点的Add标记
Add[i]=0;
}
}
点修改
void Update(int L,int C){
for(int s=N+L;s;s>>=1){
Sum[s]+=C;
}
} 点修改下的区间查询:
求A[L..R]的和(点修改没有使用Add所以不需要考虑)
代码非常简洁,也不难理解,
s和t分别代表之前的论述中的左右蓝色节点,其余的代码根据之前的论述应该很容易看懂了。
s^t^1 在s和t的父亲相同时值为0,终止循环。
两个if是判断s和t分别是左子节点还是右子节点,根据需要来计算Sum
int Query(int L,int R){
int ANS=0;
for(int s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1){
if(~s&1) ANS+=Sum[s^1];
if( t&1) ANS+=Sum[t^1];
}
return ANS;
} 区间修改:
A[L..R]+=C
//
void Update(int L,int R,int C){
int s,t,Ln=0,Rn=0,x=1;
//Ln: s一路走来已经包含了几个数
//Rn: t一路走来已经包含了几个数
//x: 本层每个节点包含几个数
for(s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1,x<<=1){
//更新Sum
Sum[s]+=C*Ln;
Sum[t]+=C*Rn;
//处理Add
if(~s&1) Add[s^1]+=C,Sum[s^1]+=C*x,Ln+=x;
if( t&1) Add[t^1]+=C,Sum[t^1]+=C*x,Rn+=x;
}
//更新上层Sum
for(;s;s>>=1,t>>=1){
Sum[s]+=C*Ln;
Sum[t]+=C*Rn;
}
} 区间修改下的区间查询:
求A[L..R]的和
int Query(int L,int R){
int s,t,Ln=0,Rn=0,x=1;
int ANS=0;
for(s=N+L-1,t=N+R+1;s^t^1;s>>=1,t>>=1,x<<=1){
//根据标记更新
if(Add[s]) ANS+=Add[s]*Ln;
if(Add[t]) ANS+=Add[t]*Rn;
//常规求和
if(~s&1) ANS+=Sum[s^1],Ln+=x;
if( t&1) ANS+=Sum[t^1],Rn+=x;
}
//处理上层标记
for(;s;s>>=1,t>>=1){
ANS+=Add[s]*Ln;
ANS+=Add[t]*Rn;
}
return ANS;
} 结合强哥讲课的内容,发现线段树很好理解,就是代码稍微复杂点而已,感觉很ok没有想象中的困难






















 795
795











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








