王道考研机试学习——并查集

什么是并查集

集合是图论问题中的一种常见的数据结构。
并查集是一种数据结构，用来表示集合信息，常用来实现确定某个集合中含有那些元素，判断某两个元素是否处于同一个集合，集合中元素的数量问题。
使用树结构来表示一些集合，且使用数组存储。
我们在数组单元i中保存结点i的双亲结点编号,如果该结点是根节点,则保存信息为-1。

并查集相关操作

查找两个元素是否处于统一集合，只需判断两个元素在数组单元中的根节点是否为同一个结点。
合并两个集合，只需要将一个集合的根节点(本来是-1)设置成另外一个集合根节点的下标即可。
查找某个节点的根节点,从该结点开始向上查找双亲结点,直至tree[x]=-1的x，这个x就是该结点的根节点。
求某个集合所含的元素个数.可以通过结构体来实现,也就是第二个例题。

并查集的优化

在两棵树的合并的时候如果不加约束，极端情况下可能造成一种斜树的情况，会使得查找效率降低。我们称这个为树的退化，
为了避免树的退化，我们在合并两棵树的时候就需要加入一定的限制条件从而保证树的高度尽可能的小。为了达到这个目的，我们在查找某个特定结点的根节点时，同时将其与根节点之间的所有结点都直接指向根节点。我们成为路径压缩

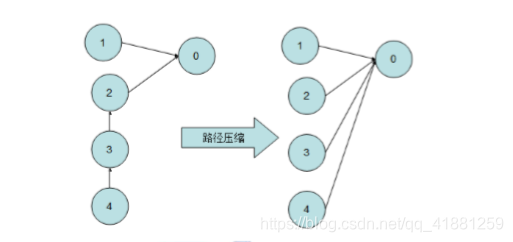
优化代码

//路径压缩后的查找情况
int findRoot(int x) {

    int tmp=x;  //tmp用于x的回溯.