C语言基础—进制表示，原码、补码、反码

---

1、进制表示

1、进制表示
进制以十进制为例：

1234.5 = 1*10^3 + 2*10^2 + 3*10^1 + 4*10^0 + 5*10^-1（按权展开求和）

• 其他进制转十进制都是按权展开求和，比如：
  十六进制：0x123 = 1*16^2 + 2*16^1 + 3*16^0

2、进制之间的转换

• 十进制转其他进制：
  • 整数部分：基数除法，倒叙取余
  • 小数部分：基础乘法，顺序取整
• 十进制转二进制：除了上面的方法，还可以“凑”，如下图：
  
• 二进制转八进制：二进制从右往左三个三个分组，然后按权展开求和，如下图
  
• 二进制转十六进制：二进制从右往左四个四个分组，然后按权展开求和，如下图：
  
• 十进制转八、十六进制：先转二进制再转八或者十六进制

【注】进制之间的转换均是以二进制为中介，这样既方便又容易理解

---

2、原码、反码、补码

对于一个数，计算机要使用一定的编码方式进行存储，原码、反码、补码是机器存储一个具体数字的编码方式
1、无符号整型数：所有的位数均表示数值：
N位无符号整型数据表示的取值范围为：0 ~ 2^N-1 (2^N表示2的N次方)

2、有符号整型数：最高位0为正数，1为负数

• 正数：原码，反码，补码三者相同（三码合一）
• 负数：其绝对值的二进制，取反，再加1，如下图：
  

3、根据二进制计算数值，假设数字为1字节：

• 无符号数全部为数值位，按权展开求和。如下图：

1010 1000 --> 1* 2^ 7+ 1*2^5 + 1* 2^ 3 = 168

• 有符号数，先看符号位确定符号，0为正数，1为负数
• 如果为正数，则按权展开求和。

0101 1000 --> 1*2^6 + 1*2^4 + 1*2^3 = 88

• 如果为负数，则先确定符号，然后取反加1计算它的绝对值。，如下图：
  

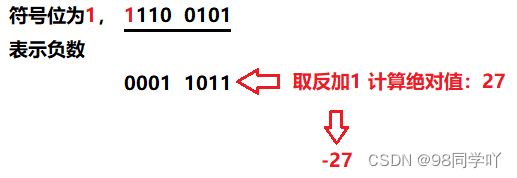
【总结】

• 将一个整数转换成二进制，就是其原码；通俗理解，原码就是一个整数本来的二进制形式
• 对于正数，它的反码就是其原码（原码和反码相同）；负数的反码是将原码中除符号位以外的所有位（数值位）取反
• 对于正数，它的补码就是其原码（正数原码、反码、补码都相同）；负数的补码就是其反码加1
• 原码、反码、补码的概念只对负数有实际意义，因为对于正数而言，原码啊、反码、补码都是一样的

在计算机内存中，整数一律采用补码的形式来存储。这意味着，当读取整数的时候还要采用逆向的转换，也就是将补码转换为原码

可见，原码、反码、补码的出现，巧妙地将符号位参与运算，并且将减法变成了加法。

3、整型数据类型

char short int long long long
  1    2  2/4  4      8

• char：-128~127共256种不同的数字
• unsigned char：0~255
• int：不加说明为4字节
• 注意数据的取值范围

---

4、浮点类型

float  double
 4      8

• 小数默认为double
• float：从左向右第一位为符号位，接下来8位位指数位，最后23位为尾数位

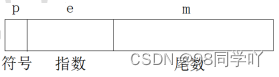
• 符号位p：0为正数，1为负
• 指数e：读取的指数 = 实际指数=127
• 尾数m：不包含小数点左边的1

举个简单的栗子：
12.5f -> 1100.1 -> 1.1001*2^3，则存储数据如下：

5、练习

1. 将十进制数转换为二进制：

2.将二进制数转换为八进制：01011010110111110011110111110101

3.将二进制数转换为十六进制：01011010110111110011110111110101

4.将十进制数转换为十六进制：50 100 134

---